




Siguiente: El espacio vectorial G
Arriba: Álgebra de Grassmann asociada
Anterior: Álgebra de Grassmann asociada
Definición 1.2
Sean 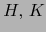 partes arbitrarias del intervalo
partes arbitrarias del intervalo ![$[\![ 1,n ]\!]$](img59.png) . Definimos
. Definimos 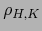 como uno de los
elementos
como uno de los
elementos 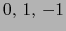 de
de  como sigue:
Los pares
como sigue:
Los pares 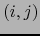 en b. los llamaremos las INVERSIONES DEL PAR
en b. los llamaremos las INVERSIONES DEL PAR 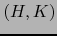 de partes ajenas de
de partes ajenas de ![$[\![ 1,n ]\!]$](img59.png) .
.
Ejemplos.
-
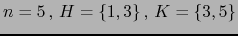 . Vale
. Vale 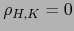 .
.
-
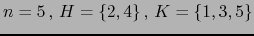 . Las inversiones del par
. Las inversiones del par 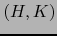 son
son
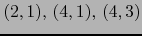 . Aquí
. Aquí 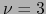 , luego
, luego
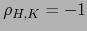 .
.
-
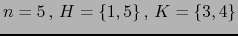 . Las inversiones del par
. Las inversiones del par 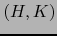 son
son 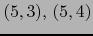 . Aquí
. Aquí 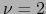 , luego
, luego 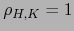 .
.
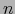 arbitrario,
arbitrario, 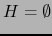 ,
, 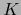 arbitrario. El número de inversiones tanto del par
arbitrario. El número de inversiones tanto del par 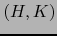 como del
par
como del
par 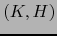 es
es 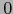 . Luego
. Luego
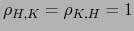 .
.
Guillermo M. Luna
2009-06-14
