




Siguiente: Elementos homogéneos del álgebra
Arriba: Álgebra de Grassmann asociada
Anterior: El símbolo
Sea G un espacio vectorial de dimensión 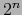 sobre
sobre  provisto de una base
provisto de una base
![${\displaystyle \left( {\overline e}_H \right)_{H \subset [\![ 1,n ]\!] } }$](img119.png) en correspondencia biyectiva con el
conjunto de todas las
en correspondencia biyectiva con el
conjunto de todas las 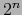 partes de
partes de ![$[\![ 1,n ]\!]$](img59.png) .
.
Aprovechando el teorema 1.1.1 hacemos de G un álgebra sobre  mediante un
producto que denotamos
mediante un
producto que denotamos
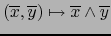 llamado
PRODUCTO EXTERIOR. Imponemos la tabla de multiplicación:
llamado
PRODUCTO EXTERIOR. Imponemos la tabla de multiplicación:
Teorema 1.2
G es un álgebra unífera. A saber, el elemento
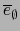 es precisamente el uno de G
es precisamente el uno de G
Demostración
Para todo
![$H\subset [\![ 1,n]\!]$](img123.png) vale
vale
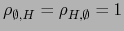 , luego por la
tabla de multiplicación:
, luego por la
tabla de multiplicación:
De ahí la conclusión por el teorema 1.1.1

Lema 1.1
![$\forall \, H,\,K,\,L \, \subset [\![ 1,n ]\!]$](img126.png) vale
vale
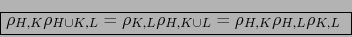 |
(8) |
Demostración
- Caso 1.
- Las partes
 no son ajenas a pares.
no son ajenas a pares.
En este caso el último miembro de la fórmula (8) vale cero. Usamos la identidad de teoría de conjuntos:
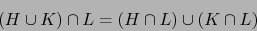 |
(9) |
Ya que por hipótesis una por lo menos de las tres intersecciones 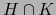 ,
, 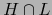 ,
, 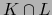 no es vacía, se sigue de (9) que bien
no es vacía, se sigue de (9) que bien 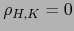 o bien
o bien
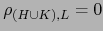 . En ambos
casos el primer miembro de la fórmula (8) es cero. Análogamente el segundo miembro de dicha fórmula
vale cero. Luego la fórmula (8) es correcta.
. En ambos
casos el primer miembro de la fórmula (8) es cero. Análogamente el segundo miembro de dicha fórmula
vale cero. Luego la fórmula (8) es correcta.
- Caso 2.
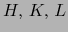 son ajenos a pares.
son ajenos a pares.
Para probar que el primer miembro de (8) es igual al tercero debemos probar:
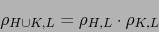 |
(10) |
Sea  el número de pares
el número de pares 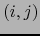 con
con
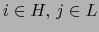 tales que
tales que 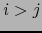 .
Sea
.
Sea 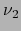 el número de pares
el número de pares 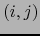 con
con
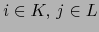 tales que
tales que 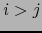 . Ya que
. Ya que
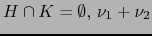 es el número de inversiones del par
es el número de inversiones del par 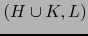 , luego:
, luego:
probando (10). Análogamente se prueba que el segundo miembro de la fórmula (8) es igual al tercero.

Teorema 1.3
G es un álgebra asociativa sobre  .
.
Demostración
Para tres partes arbitrarias 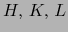 de
de ![$[\![ 1,n ]\!]$](img59.png) tenemos en virtud de la tabla de
multiplicación:
tenemos en virtud de la tabla de
multiplicación:
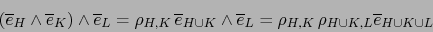 |
(11) |
y
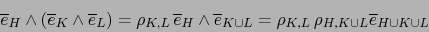 |
(12) |
De (11) y (12) y del lema 1.1.1 se deduce:
De ahí la conclusión deseada, por el teorema 1.1.1






Siguiente: Elementos homogéneos del álgebra
Arriba: Álgebra de Grassmann asociada
Anterior: El símbolo
Guillermo M. Luna
2009-06-14
![]() sobre
sobre ![]() provisto de una base
provisto de una base
![]() en correspondencia biyectiva con el
conjunto de todas las
en correspondencia biyectiva con el
conjunto de todas las ![]() partes de
partes de ![]() .
.
![]() mediante un
producto que denotamos
mediante un
producto que denotamos
![]() llamado
PRODUCTO EXTERIOR. Imponemos la tabla de multiplicación:
llamado
PRODUCTO EXTERIOR. Imponemos la tabla de multiplicación:
![]() vale
vale
![]() , luego por la
tabla de multiplicación:
, luego por la
tabla de multiplicación:
![]() el número de pares
el número de pares ![]() con
con
![]() tales que
tales que ![]() .
Sea
.
Sea ![]() el número de pares
el número de pares ![]() con
con
![]() tales que
tales que ![]() . Ya que
. Ya que
![]() es el número de inversiones del par
es el número de inversiones del par ![]() , luego:
, luego:
![]() de
de ![]() tenemos en virtud de la tabla de
multiplicación:
tenemos en virtud de la tabla de
multiplicación: