




Siguiente: El símbolo
Arriba: Álgebra exterior sobre un
Anterior: Álgebra exterior sobre un
Álgebra de Grassmann asociada a una base
Nota
En el presente capítulo se considerará espacios vectoriales sobre un cuerpo conmutativo  . Si se razona sobre varios espacios vectoriales, será sobreentendido que el cuerpo
. Si se razona sobre varios espacios vectoriales, será sobreentendido que el cuerpo  es el mismo para todos dichos espacios vectoriales.
es el mismo para todos dichos espacios vectoriales.
Los elementos de  los llamaremos ocasionalmente ESCALARES conforme a una costumbre bastante generalizada actualmente. Los elementos de diferentes espacios vectoriales considerados se llamarán VECTORES y se designarán en general por letras con flechas encima.
los llamaremos ocasionalmente ESCALARES conforme a una costumbre bastante generalizada actualmente. Los elementos de diferentes espacios vectoriales considerados se llamarán VECTORES y se designarán en general por letras con flechas encima.
Vamos a recordar un método simple para construir álgebras de rango finito (es decir de dimensión finita como espacio vectorial) sobre un cuerpo conmutativo  .
.
Teorema 1.1
Sea  un espacio vectorial de dimensión finita sobre un cuerpo conmutativo
un espacio vectorial de dimensión finita sobre un cuerpo conmutativo
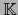 , provisto de una base
, provisto de una base
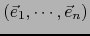 . Sea
. Sea
 , con índices
, con índices
![$i,j,k \in [\![ 1,n]\!]$](img58.png) , una familia arbitraria de elementos de
, una familia arbitraria de elementos de  . (Aquí como en todo el libro
. (Aquí como en todo el libro ![$[\![ 1,n ]\!]$](img59.png) designa el correspondiente intervalo en
designa el correspondiente intervalo en 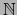 , es decir, el conjunto
, es decir, el conjunto
 de enteros naturales).
de enteros naturales).
- Existe una y una sola aplicación bilineal
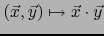 de
de 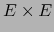 en
en  que verifica la TABLA DE MULTIPLICACIÓN:
que verifica la TABLA DE MULTIPLICACIÓN:
- Un vector
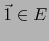 es el elemento uno del álgebra
es el elemento uno del álgebra  si y sólo si:
si y sólo si:
- El álgebra
 es asociativa si y sólo si vale:
es asociativa si y sólo si vale:
Equivalentemente:
- El álgebra
 es conmutativa si y sólo si:
es conmutativa si y sólo si:
Equivalentemente:
Demostración
- Unicidad del álgebra.
Supongamos la existencia de una multiplicación
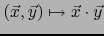 en
en  conforme a la tabla de multiplicación.
Sean
conforme a la tabla de multiplicación.
Sean
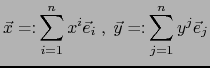
![[*]](footnote.png) vectores arbitrarios en
vectores arbitrarios en  .
.
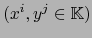 . Por la bilinealidad de la multiplicación vale:
. Por la bilinealidad de la multiplicación vale:
de donde por la tabla de multiplicación:
 |
(1) |
El segundo miembro de (1) expresa el producto
 sin ambigüedad. Así pues, si el álgebra deseada existe, es única.
sin ambigüedad. Así pues, si el álgebra deseada existe, es única.
- Existencia del álgebra.
Definimos la aplicación
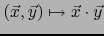 de
de 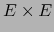 en
en  por la fórmula (1) . Consideremos tres vectores:
por la fórmula (1) . Consideremos tres vectores:
y dos escalares
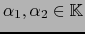 .
.
Vale
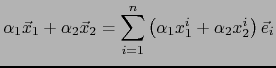 de donde aplicando (1):
de donde aplicando (1):
Análogamente se prueba la ley:
Así pues la aplicación
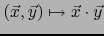 es bilineal. Resta probar que es conforme a la tabla de multiplicación. Ahora bien,
usando las ``deltas de Kronecker'' podemos escribir
es bilineal. Resta probar que es conforme a la tabla de multiplicación. Ahora bien,
usando las ``deltas de Kronecker'' podemos escribir
![$\forall \,l,m \in [\![ 1,n ]\!]$](img78.png) :
:
de donde, aplicando (1):
Así se ha probado la existencia del álgebra deseada.
- Supongamos que existe
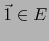 tal que
tal que
![$\vec{1} \cdot \vec{e}_i = \vec{e}_i \cdot \vec{1} =\vec{e}_i \quad \forall \, i \in [\![ 1,n ]\!]$](img81.png) .
Si
.
Si
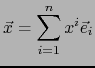 es un vector arbitrario de
es un vector arbitrario de  , vale:
, vale:
Así pues 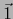 es el elemento uno de
es el elemento uno de  .
.
- Supongamos que valen las relaciones:
 |
(2) |
Consideremos tres vectores arbitrarios:
Por la bilinealidad de la multiplicación tenemos:
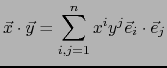 y:
y:
 |
(3) |
Análogamente:
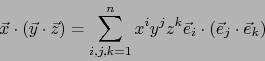 |
(4) |
De (3), (4) y (2) se sigue:
Vale decir que el álgebra  es un álgebra asociativa.
es un álgebra asociativa.
- Suponemos que valen las relaciones:
![\begin{displaymath}
\vec{e}_i \cdot \vec{e}_j = \vec{e}_j \cdot \vec{e}_i \quad \forall \, i,j \in [\![ 1,n ]\!]
\end{displaymath}](img90.png) |
(5) |
Para dos vectores arbitrarios:
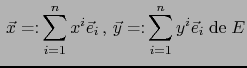 vale:
vale:
De (6), (7) y (5) obtenemos:
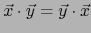 .
Así pues,
.
Así pues,  es un álgebra conmutativa.
es un álgebra conmutativa.

Sea  un cuerpo conmutativo. Fijemos
un cuerpo conmutativo. Fijemos
 . Usando el
procedimiento general suministrado por el teorema precedente vamos a
construir un álgebra de dimensión
. Usando el
procedimiento general suministrado por el teorema precedente vamos a
construir un álgebra de dimensión 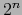 que provisionalmente llamaremos
G (por ``Grassmann'').
que provisionalmente llamaremos
G (por ``Grassmann'').
Subsections





Siguiente: El símbolo
Arriba: Álgebra exterior sobre un
Anterior: Álgebra exterior sobre un
Guillermo M. Luna
2009-06-14
![]() . Si se razona sobre varios espacios vectoriales, será sobreentendido que el cuerpo
. Si se razona sobre varios espacios vectoriales, será sobreentendido que el cuerpo ![]() es el mismo para todos dichos espacios vectoriales.
es el mismo para todos dichos espacios vectoriales.
![]() los llamaremos ocasionalmente ESCALARES conforme a una costumbre bastante generalizada actualmente. Los elementos de diferentes espacios vectoriales considerados se llamarán VECTORES y se designarán en general por letras con flechas encima.
los llamaremos ocasionalmente ESCALARES conforme a una costumbre bastante generalizada actualmente. Los elementos de diferentes espacios vectoriales considerados se llamarán VECTORES y se designarán en general por letras con flechas encima.
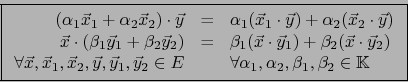
![]() .
.
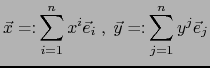
![[*]](footnote.png) vectores arbitrarios en
vectores arbitrarios en 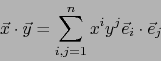
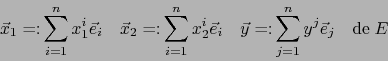
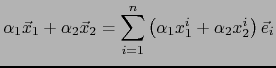 de donde aplicando (1):
de donde aplicando (1):
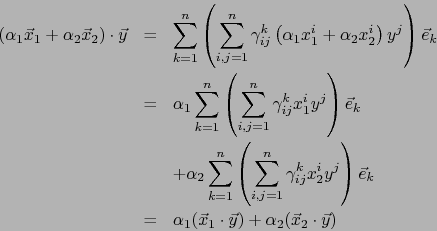

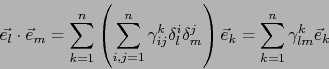
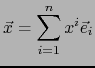 es un vector arbitrario de
es un vector arbitrario de 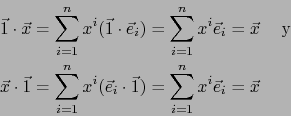
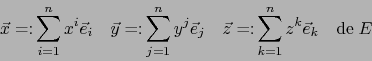
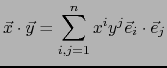 y:
y:
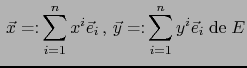 vale:
vale:
![]() un cuerpo conmutativo. Fijemos
un cuerpo conmutativo. Fijemos
![]() . Usando el
procedimiento general suministrado por el teorema precedente vamos a
construir un álgebra de dimensión
. Usando el
procedimiento general suministrado por el teorema precedente vamos a
construir un álgebra de dimensión ![]() que provisionalmente llamaremos
G (por ``Grassmann'').
que provisionalmente llamaremos
G (por ``Grassmann'').