




Siguiente: El espacio proyectivo
Arriba: Ejemplos de variedades diferenciables
Anterior: Espacios afines normados de
La esfera 
Sea
 . Designamos por
. Designamos por  la esfera euclidiana de centro 0, de
radio 1 en
la esfera euclidiana de centro 0, de
radio 1 en
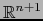 , o sea:
, o sea:
La topología de  será aquella inducida por la topología usual de
será aquella inducida por la topología usual de
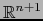 .
.
 es la imagen inversa del solo punto
es la imagen inversa del solo punto  por la aplicación continua
por la aplicación continua
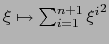 de
de
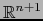 en
en 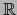 . Luego
. Luego
 es un subconjunto cerrado de
es un subconjunto cerrado de
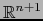 . Es también obviamente acotado, luego,
. Es también obviamente acotado, luego,
 es un espacio compacto.
es un espacio compacto.
Sea  la norma euclidiana en
la norma euclidiana en
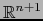 .
.  es la imagen
de
es la imagen
de
 por la aplicación continua
por la aplicación continua
 de
de
 en
en
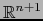 .
Si probamos que
.
Si probamos que
 es un conjunto conexo, vendrá, pues, demostrado que
lo es también
es un conjunto conexo, vendrá, pues, demostrado que
lo es también  .
.
Observamos que si 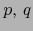 son puntos distintos de
son puntos distintos de
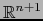 , el segmento:
, el segmento:
imagen homeomorfa del intervalo ![$[0,1]$](img4420.png) de
de 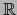 por la aplicación
por la aplicación
 , es un conjunto conexo. Sean
, es un conjunto conexo. Sean 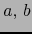 puntos
distintos de
puntos
distintos de
 .
.
- Si
![$ 0 \notin [a,b]$](img4422.png) , el segmento
, el segmento ![$[a,b]$](img3002.png) está contenido en
está contenido en
 .
.
- Supongamos
![$0 \in [a,b]$](img4423.png) . Sea
. Sea  un punto de
un punto de
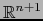 fuera de la recta
fuera de la recta
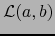 (la recta que pasa por los puntos
(la recta que pasa por los puntos 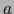 ,
, 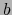 ). Las rectas
). Las rectas
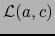 y
y 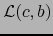 son distintas de
son distintas de 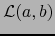 , luego
los segmentos
, luego
los segmentos ![$[a,c]$](img4428.png) y
y ![$[c,b]$](img4429.png) y, por lo tanto, el conjunto conexo
y, por lo tanto, el conjunto conexo
![$[a,c] \cup [c,b]$](img4430.png) están contenidos en
están contenidos en
 .
.
En los dos casos a) y b) existe un conjunto conexo contenido en
 , al cual pertenecen los puntos
, al cual pertenecen los puntos 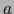 y
y 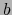 . Así pues,
. Así pues,
 es un conjunto conexo, luego,
es un conjunto conexo, luego,
 es un espacio conexo.
es un espacio conexo.
Procedemos a construir sobre  un atlas coherente
un atlas coherente  .
.
![$\forall \, i \in [\![ 1, n+1 ]\!]$](img4431.png) definamos las partes
definamos las partes
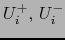 de
de  como sigue:
como sigue:
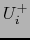 y
y 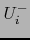 son las intersecciones de
son las intersecciones de  con sendos semiespacios:
con sendos semiespacios:
Puesto
que dichos semiespacios son conjuntos abiertos en
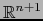 ,
, 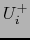 y
y 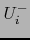 son partes
abiertas de
son partes
abiertas de  .
.
Sea 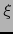 un punto arbitrario de
un punto arbitrario de  . Puesto que
. Puesto que
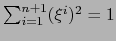 ,
,
![$\exists \, i \in [\![ 1, n+1 ]\!]$](img4439.png) tal que
tal que 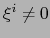 , luego
, luego 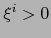 ó
ó 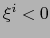 . En el
primer caso
. En el
primer caso 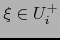 y en el segundo caso
y en el segundo caso 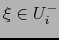 . Por lo tanto:
Los
. Por lo tanto:
Los 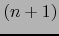 conjuntos
conjuntos 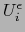 ,
,
![$i \in [\![ 1,n+1 ]\!]$](img4447.png) ,
,
 , constituyen
un recubrimiento abierto de
, constituyen
un recubrimiento abierto de  .
.
Designamos por 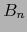 la bola euclidiana abierta de centro
la bola euclidiana abierta de centro 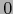 de radio
de radio  en
en
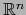 , o sea:
, o sea:
![$\forall \, i [\![ 1,n+1 ]\!]$](img4450.png) y para
y para
 , definimos la aplicación
, definimos la aplicación
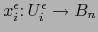 por:
por:
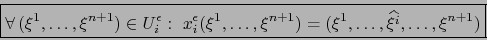 |
(4) |
El acento cirunflejo sobre 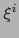 indica que
indica que 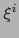 se debe omitir de la sucesión.
se debe omitir de la sucesión.
Por ser
 se tiene
se tiene
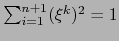 y
y 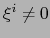 , luego efectivamente:
, luego efectivamente:
Dado un punto arbitrario
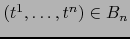 , existe un único punto
, existe un único punto
 tal que
tal que
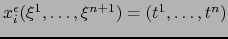 , a saber el
punto:
, a saber el
punto:
Así pues, la aplicación 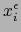 es una biyección de
es una biyección de 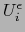 sobre
la bola
sobre
la bola 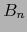 . La aplicación inversa se define por:
. La aplicación inversa se define por:
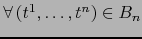
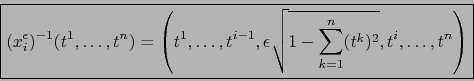 |
(5) |
La proyección
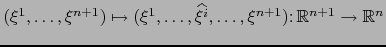 es una aplicación continua. Por la fórmula (4) la aplicación
es una aplicación continua. Por la fórmula (4) la aplicación 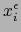 considerada como
aplicación con valores en
considerada como
aplicación con valores en
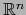 , restricción de dicha proyección al conjunto
, restricción de dicha proyección al conjunto
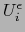 , es también continua y sigue siendo continua, si la consideramos
como una aplicación
, es también continua y sigue siendo continua, si la consideramos
como una aplicación
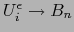 . La fórmula (4) muestra que
. La fórmula (4) muestra que
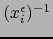 considerada ella como aplicación
considerada ella como aplicación
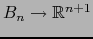 es continua. Sigue siendo continua, si la
consideramos como aplicación
es continua. Sigue siendo continua, si la
consideramos como aplicación
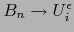 . En resumidas cuentas:
. En resumidas cuentas:
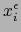 es homeomorfismo de
es homeomorfismo de 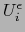 sobre el abierto
sobre el abierto 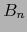 de
de
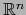 .
La familia
.
La familia
![$\left( U_i^\epsilon, x_i^\epsilon, n\right)_{i \in [\![ 1,n+1 ]\!] }^{\epsilon = \pm 1}$](img4468.png) es pues
un atlas sobre el espacio topológico
es pues
un atlas sobre el espacio topológico  .
.
Consideremos los cambios de mapas:
Cabe suponer 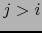 . Con esta hipótesis tenemos por las fórmulas (4) y (5):
. Con esta hipótesis tenemos por las fórmulas (4) y (5):
Ya que para
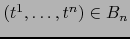 vale
vale
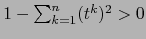 las fórmulas (6) y (7) muestran que los cambios de mapas
las fórmulas (6) y (7) muestran que los cambios de mapas
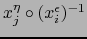 y
y
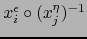 son aplicaciones de clase
son aplicaciones de clase  .
En conclusión
.
En conclusión
El altas
![$\left( U_i^\epsilon, x_i^\epsilon, n \right)_{i \in [\![ 1,n ]\!]}^{\epsilon = \pm 1}$](img4480.png) es un atlas
coherente
es un atlas
coherente  . Define sobre
. Define sobre  la estructura de una variedad
la estructura de una variedad  de dimensión
de dimensión  .
.
Ésta se llama ESTRUCTURA NATURAL DE VARIEDAD DIFERENCIAL sobre  .
.





Siguiente: El espacio proyectivo
Arriba: Ejemplos de variedades diferenciables
Anterior: Espacios afines normados de
Guillermo M. Luna
2009-06-14
![]() . Designamos por
. Designamos por ![]() la esfera euclidiana de centro 0, de
radio 1 en
la esfera euclidiana de centro 0, de
radio 1 en
![]() , o sea:
, o sea:
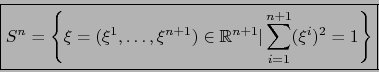
![]() es la imagen inversa del solo punto
es la imagen inversa del solo punto ![]() por la aplicación continua
por la aplicación continua ![]() de
de
![]() en
en ![]() . Luego
. Luego
![]() es un subconjunto cerrado de
es un subconjunto cerrado de
![]() . Es también obviamente acotado, luego,
. Es también obviamente acotado, luego,
![]() es un espacio compacto.
es un espacio compacto.
![]() la norma euclidiana en
la norma euclidiana en
![]() .
. ![]() es la imagen
de
es la imagen
de
![]() por la aplicación continua
por la aplicación continua
![]() de
de
![]() en
en
![]() .
Si probamos que
.
Si probamos que
![]() es un conjunto conexo, vendrá, pues, demostrado que
lo es también
es un conjunto conexo, vendrá, pues, demostrado que
lo es también ![]() .
.
![]() son puntos distintos de
son puntos distintos de
![]() , el segmento:
, el segmento:
![]() un atlas coherente
un atlas coherente ![]() .
.
![]() definamos las partes
definamos las partes
![]() de
de ![]() como sigue:
como sigue:

![]() un punto arbitrario de
un punto arbitrario de ![]() . Puesto que
. Puesto que
![]() ,
, ![]() tal que
tal que ![]() , luego
, luego ![]() ó
ó ![]() . En el
primer caso
. En el
primer caso ![]() y en el segundo caso
y en el segundo caso ![]() . Por lo tanto:
Los
. Por lo tanto:
Los ![]() conjuntos
conjuntos ![]() ,
,
![]() ,
,
![]() , constituyen
un recubrimiento abierto de
, constituyen
un recubrimiento abierto de ![]() .
.
![]() la bola euclidiana abierta de centro
la bola euclidiana abierta de centro ![]() de radio
de radio ![]() en
en
![]() , o sea:
, o sea:

![]() se tiene
se tiene
![]() y
y ![]() , luego efectivamente:
, luego efectivamente: 
es homeomorfismo de
sobre el abierto
de
. La familia
es pues un atlas sobre el espacio topológico
.
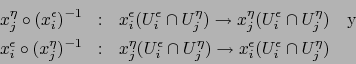
es un atlas coherente
. Define sobre
la estructura de una variedad
de dimensión
.