Sean ![]() un espacio afín normado real de dimensión finita
un espacio afín normado real de dimensión finita ![]() y
y
![]() su espacio vectorial asociado. Sabemos del teorema 4.2.3 que todas las
normas sobre
su espacio vectorial asociado. Sabemos del teorema 4.2.3 que todas las
normas sobre ![]() definen la misma topología sobre el espacio afín
definen la misma topología sobre el espacio afín
![]() , la ``topología natural'' de
, la ``topología natural'' de ![]() .
.
Sean
![]() un referencial arbitrario de
un referencial arbitrario de ![]() y
y
![]() la biyección:
la biyección:

 y
y
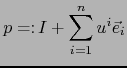 son puntos arbitrarios de
son puntos arbitrarios de 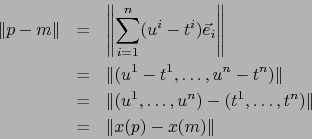
Los mapas de ![]() obtenidos de este modo mediante los referenciales de
obtenidos de este modo mediante los referenciales de
![]() , los llamaremos los MAPAS AFINES de
, los llamaremos los MAPAS AFINES de ![]() .
.
Demostración
Desigaremos por
![]() la base natural
de
la base natural
de
![]() . Sean
. Sean
![]() una referencial en
una referencial en ![]() y
y ![]() la única aplicación lineal de
la única aplicación lineal de ![]() en
en
![]() tal que
tal que
![]() .
.
Sea ![]() el mapa afín de
el mapa afín de ![]() definido por el referencial
definido por el referencial
![]() . Vale:
. Vale:
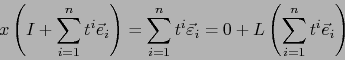
Siendo ![]() de hecho un isomorfismo afín de
de hecho un isomorfismo afín de ![]() sobre
sobre
![]() , se
sigue del teorema 4.1.7 que
, se
sigue del teorema 4.1.7 que ![]() es un isomorfismo afín de
es un isomorfismo afín de
![]() sobre
sobre ![]() . De nuevo, por el teorema 4.5.4
. De nuevo, por el teorema 4.5.4 ![]() es una aplicación de clase
es una aplicación de clase ![]() .
.
Sean ahora
![]() dos mapas afines de
dos mapas afines de ![]() . Por lo
probado, las aplicaciones
. Por lo
probado, las aplicaciones
![]() ,
,
![]() ,
,
![]() ,
,
![]() son de
clase
son de
clase ![]() (C.D.). Por el teorema 4.5.5 los cambios de mapas
(C.D.). Por el teorema 4.5.5 los cambios de mapas
![]() y
y
![]() son de clase
son de clase ![]() .
Se puede también observar que dichos cambios de mapas son isomorfismos afines
de
.
Se puede también observar que dichos cambios de mapas son isomorfismos afines
de
![]() sobre
sobre
![]() y aplicar otra vez el teorema 4.5.4.
Con ambos métodos viene probado que los mapas
y aplicar otra vez el teorema 4.5.4.
Con ambos métodos viene probado que los mapas ![]() y
y ![]() son compatibles
son compatibles ![]() .
.
![]()
Se llama la ESTRUCTURA NATURAL DE VARIEDAD ![]() sobre
sobre ![]() .
.
A menos de una indicación contraria, será la única considerada sobre ![]() .
.
Sobre los abiertos de ![]() se considerará la correspondiente estructura
de subvariedades abiertas.
se considerará la correspondiente estructura
de subvariedades abiertas.
Demostración
Usamos un mapa ![]() de
de ![]() , restricción de un mapa afín de
, restricción de un mapa afín de
![]() y un mapa afín
y un mapa afín ![]() de
de ![]() . Según la demostración del teorema 5.4.1 las aplicaciones
. Según la demostración del teorema 5.4.1 las aplicaciones
![]() e
e
![]() y
también
y
también ![]() e
e ![]() son de clase
son de clase ![]() (C.D.). (Aquí
(C.D.). (Aquí
![]() .).
La aplicación
.).
La aplicación ![]() leída en dichos mapas es:
leída en dichos mapas es:
Supongamos que ![]() es diferenciable en
es diferenciable en ![]() (C.D.). Ya que
(C.D.). Ya que
![]() es diferenciable (C.D.) en
es diferenciable (C.D.) en ![]() e
e ![]() es diferenciable C.D. en
es diferenciable C.D. en
![]() se sigue de (2) y del teorema 4.4.4 que
se sigue de (2) y del teorema 4.4.4 que
![]() es diferenciable C.D. en
es diferenciable C.D. en ![]() . Vale decir,
. Vale decir, ![]() es diferenciable en
es diferenciable en ![]() según la definición 5.2.1.
según la definición 5.2.1.
Si ![]() es de clase
es de clase ![]() en
en ![]() (C.D.) se sigue de (2) y del teorema 4.5.5,
que
(C.D.) se sigue de (2) y del teorema 4.5.5,
que
![]() es de clase
es de clase ![]() (C.D.) en
(C.D.) en ![]() . Luego
. Luego ![]() es de clase
es de clase ![]() según la definición 5.2.2.
según la definición 5.2.2.
La relación (2) puede escribirse equivalentemente:
Supongamos ![]() de clase
de clase ![]() en
en ![]() según la definición
5.2.2. Esto significa que
según la definición
5.2.2. Esto significa que
![]() es de clase
es de clase ![]() (C.D.)
en
(C.D.)
en ![]() . Por (2) y el teorema 4.53
. Por (2) y el teorema 4.53 ![]() es de clase
es de clase ![]() (C.D.) en
(C.D.) en ![]() .
.
![]()