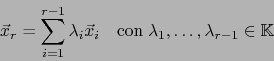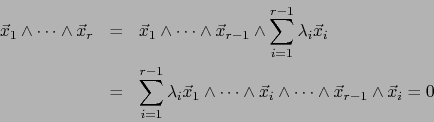Gracias al último teorema y el teorema 1.3.2 sobre la unicidad esencial del álgebra exterior estamos en posición de precisar la estructura de una álgebra exterior arbitraria sobre un espacio vectorial de dimensión finita.
Sean ![]() un espacio vectorial de dimensión finita sobre un cuerpo conmutativo
un espacio vectorial de dimensión finita sobre un cuerpo conmutativo ![]() y
y
![]() una base arbitrariamente elegida en
una base arbitrariamente elegida en ![]() . Sea G el álgebra de Grassmann sobre
. Sea G el álgebra de Grassmann sobre ![]() asociada con dicha base.
asociada con dicha base.
![]() designará la inyección canónica. La multiplicación en G la designaremos aquí por
el símbolo
designará la inyección canónica. La multiplicación en G la designaremos aquí por
el símbolo
![]() . Por el teorema 1.3.3
. Por el teorema 1.3.3
![]() es un álgebra exterior sobre
es un álgebra exterior sobre ![]() . Consideramos también un álgebra exterior
. Consideramos también un álgebra exterior
![]() sobre
sobre ![]() construída de cualquier manera. La notación
construída de cualquier manera. La notación ![]() para un álgebra exterior es actualmente clásica. La multiplicación en el álgebra
para un álgebra exterior es actualmente clásica. La multiplicación en el álgebra ![]() la designamos por el símbolo
la designamos por el símbolo ![]() . Seguiremos llamándola MULTIPLICACIÓN EXTERIOR.
. Seguiremos llamándola MULTIPLICACIÓN EXTERIOR.
Por el teorema 1.3.2 existe un único isomorfismo ![]() del álgebra G sobre el álgebra
del álgebra G sobre el álgebra ![]() tal que:
tal que:
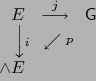
Una vez para siempre convenimos en identificar el subespacio vectorial ![]() del álgebra
del álgebra ![]() con
con ![]() , vale decir todo elemento
, vale decir todo elemento
![]() de
de ![]() con
con ![]() . Mediante este convenio
el espacio vectorial
. Mediante este convenio
el espacio vectorial ![]() llega a ser un subespacio vectorial del álgebra
llega a ser un subespacio vectorial del álgebra ![]() . Dado que un convenio análogo ya fue hecho para
. Dado que un convenio análogo ya fue hecho para ![]() en §1, la relación (21) reza ahora simplemente:
en §1, la relación (21) reza ahora simplemente:
![]() y
y
![]() vale la regla:
vale la regla:
La relación (24) afirma que la multiplicación de un elemento de ![]() por un elemento
por un elemento ![]() es un caso particular de la multiplicación exterior. En particular
es un caso particular de la multiplicación exterior. En particular
![]() es el elemento uno del álgebra
es el elemento uno del álgebra ![]() .
.
Sabemos que los ![]() elementos
elementos ![]() y
y
![]()
![]() , constituyen una base de G. Puesto que
, constituyen una base de G. Puesto que ![]() y
y
![]() , vemos que, cualquiera que fuese la base
, vemos que, cualquiera que fuese la base
![]() de
de ![]() , los
, los ![]() elementos
elementos ![]() y
y
![]() ,
,
![]() constituyen una base de
constituyen una base de ![]() .
.
De esto se sigue:
![]() es el subespacio vectorial de G engendrado linealmente por el conjunto de todos los productos
es el subespacio vectorial de G engendrado linealmente por el conjunto de todos los productos
![]() con
con
![]() . Designamos por
. Designamos por
![]() el subespacio vectorial de
el subespacio vectorial de ![]() engendrado linealmente por el conjunto de todos los productos
engendrado linealmente por el conjunto de todos los productos
![]() con
con
![]() . Ponemos por definición:
. Ponemos por definición:
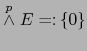 si
si

Al poner
![]() seguiremos escribiendo
seguiremos escribiendo
![]() por
por
![]() como lo hacíamos para el álgebra de Grassmann. Los elementos
como lo hacíamos para el álgebra de Grassmann. Los elementos
![]() obedecen a la tabla de multiplicación
obedecen a la tabla de multiplicación
En efecto, según el teorema 1.3.2 esta última es esencialmente única, en particular ya independiente de la elección de
cualquier base de ![]() . Está pues ligada ``canónicamente'' con
. Está pues ligada ``canónicamente'' con ![]() .
.
El recurso de la ``propiedad universal'' nos sirvió precisamente para liberarnos de la molesta dependencia de bases en la definición inicial. El éxito fue completo. Como dirían familiarmente algunos matemáticos, todo parece indicar que el álgebra exterior no es una creación artificial sino que ``existe en la naturaleza''.
Esta impresión se corrobora mucho por el simple e importante:
Demostración