En el §1 a toda base de un espacio vectorial ![]() de dimensión finita le asociamos un ``álgebra de Grassmann'' sobre
de dimensión finita le asociamos un ``álgebra de Grassmann'' sobre ![]() . Pueden cabernos dudas acerca de la utilidad de esa construcción, pues, hasta el momento, no vemos como se relacionan entre sí estas diferentes álgebras y por ello nuestra construcción carece de carácter ``intrínseco''. Este defecto vendrá eliminado en la presente sección. Vamos a ver en efecto que todas
las álgebras de Grassmann consideradas pueden identificarse con una sola álgebra que llamaremos ``álgebra exterior'' sobre
. Pueden cabernos dudas acerca de la utilidad de esa construcción, pues, hasta el momento, no vemos como se relacionan entre sí estas diferentes álgebras y por ello nuestra construcción carece de carácter ``intrínseco''. Este defecto vendrá eliminado en la presente sección. Vamos a ver en efecto que todas
las álgebras de Grassmann consideradas pueden identificarse con una sola álgebra que llamaremos ``álgebra exterior'' sobre ![]() , ya independiente de toda elección de una base en
, ya independiente de toda elección de una base en ![]() .
.
Para simplificar el lenguaje adoptaremos el siguiente:
Convenio

Aquí
![]() y
y
![]() son los ``elementos uno'' de sendas álgebras
son los ``elementos uno'' de sendas álgebras ![]() y
y ![]() .
.
Si además ![]() es una biyección de
es una biyección de ![]() sobre
sobre ![]()
![]() se dice un ISOMORFISMO del álgebra
se dice un ISOMORFISMO del álgebra ![]() sobre el álgebra
sobre el álgebra ![]() .
.
Demostración
Aplicaremos el teorema 1.2.4.
![]() consideramos el entero
consideramos el entero ![]() , número mínimo de trasposiciones de dígitos consecutivos cuyo producto es
, número mínimo de trasposiciones de dígitos consecutivos cuyo producto es ![]() . La demostración se hará por inducción sobre
. La demostración se hará por inducción sobre ![]() .
.
En este caso ![]() es una trasposición de dígitos consecutivos:
es una trasposición de dígitos consecutivos:
Sea
![]() donde
donde
![]() son trasposiciones
de dígitos consecutivos y
son trasposiciones
de dígitos consecutivos y ![]() es el entero mínimo para el cual tal representación es posible. Pongamos:
es el entero mínimo para el cual tal representación es posible. Pongamos:
Por otra parte, por hipótesis de inducción vale:
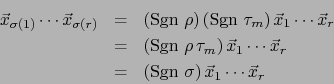
Demostración
Sean
![]() tales que
tales que ![]() y
y
![]() . Sea
. Sea
![]() una permutación que satisface:
una permutación que satisface:

Ejemplo
Sean ![]() un espacio vectorial de dimensión finita y G el álgebra de Grassmann asociada con una base de
un espacio vectorial de dimensión finita y G el álgebra de Grassmann asociada con una base de ![]() . En virtud del teorema 1.1.6 G es una álgebra alternada sobre su subespacio vectorial E.
. En virtud del teorema 1.1.6 G es una álgebra alternada sobre su subespacio vectorial E.
Así pues si
![]() y
y
![]() , vale:
, vale:
Observación
Sea ![]() una aplicación lineal alternante de un espacio vectorial
una aplicación lineal alternante de un espacio vectorial ![]() en un álgebra
en un álgebra ![]() . Por el teorema 1.3.1
y su corolario:
. Por el teorema 1.3.1
y su corolario:
La terna
![]() se llama ´ALGEBRA EXTERIOR SOBRE EL ESPACIO VECTORIAL si:
se llama ´ALGEBRA EXTERIOR SOBRE EL ESPACIO VECTORIAL si:
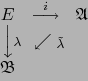
Por un abuso de lenguaje bien común en matemática (aunque lógicamente objetable) se dice simplemente que ``![]() es un álgebra exterior sobre el espacio vectorial
es un álgebra exterior sobre el espacio vectorial ![]() ''.
''.
La propiedad (6) se llama PROPIEDAD UNIVERSAL DEL ÁLGEBRA EXTERIOR. ![[*]](footnote.png)
Nota
Pronto veremos que si
![]() es un álgebra exterior sobre
es un álgebra exterior sobre ![]() , la aplicación lineal alternante
, la aplicación lineal alternante
![]() es necesariamente inyectiva. Si identificamos mediante ella
es necesariamente inyectiva. Si identificamos mediante ella ![]() con
con ![]() ,
, ![]() llega a ser un subespacio vectorial del álgebra
llega a ser un subespacio vectorial del álgebra ![]() . Con este convenio, la propiedad universal (
. Con este convenio, la propiedad universal (![]() ) se enuncia más simplemente (y quizá más intuitivamente) como sigue:
) se enuncia más simplemente (y quizá más intuitivamente) como sigue:

Si
![]() es otra álgebra exterior sobre E, existe un único isomorfismo
es otra álgebra exterior sobre E, existe un único isomorfismo ![]() del álgebra
del álgebra
![]() sobre el álgebra
sobre el álgebra
![]() tal que:
tal que:
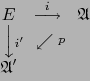
Nota
Para interpretar intuitivamente este resultado, podemos imaginar que los elementos de
![]() son los mismos elementos de
son los mismos elementos de ![]() pero nombrados en un idioma distinto, siendo el isomorfismo
pero nombrados en un idioma distinto, siendo el isomorfismo ![]() un diccionario que efectua la traducción.
un diccionario que efectua la traducción. ![]() traduce también la aplicación lineal alternante
traduce también la aplicación lineal alternante ![]() por
por ![]() en el sentido de que
en el sentido de que
![]() se traduce por
se traduce por
![]() .
.
Si, adelantando las cosas, consideramos ![]() como subespacio vectorial tanto de
como subespacio vectorial tanto de ![]() como de
como de
![]() , la última condición se expresa simplemente diciendo que ``
, la última condición se expresa simplemente diciendo que ``![]() preserva los elementos de
preserva los elementos de ![]() ''.
''.
Demostración
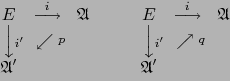
Aplicamos la propiedad universal a la terna
![]() , tomando
, tomando
![]() en papel de
en papel de ![]() e
e ![]() en papel de
en papel de ![]() . Por dicha propiedad universal existe un único homomorfismo
. Por dicha propiedad universal existe un único homomorfismo ![]() del álgebra
del álgebra ![]() en el álgebra
en el álgebra
![]() que cumple:
que cumple:
Apliquemos otra vez la propiedad universal de la terna
![]() tomando ahora el propio
tomando ahora el propio ![]() en el papel de
en el papel de ![]() e
e ![]() en el papel de
en el papel de ![]() . Por dicha propiedad universal existe un único homomorfismo del álgebra
. Por dicha propiedad universal existe un único homomorfismo del álgebra ![]() en sí que hace conmutativo el diagrama:
en sí que hace conmutativo el diagrama:
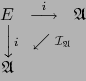
Pasamos al asunto de la existencia del álgebra exterior. Dicha existencia puede probarse para cualquier espacio vectorial y aun en condiciones más generales, pero aquí nos limitaremos al caso de un espacio vectorial de dimensión finita.
Demostración
![]() vale por el teorema (1.1.6):
vale por el teorema (1.1.6):
Sea pues ![]() una aplicación lineal alternante de
una aplicación lineal alternante de ![]() en un álgebra
en un álgebra ![]() arbitraria. Hay que demostrar que
arbitraria. Hay que demostrar que ![]() puede ampliarse a un único homomorfismo
puede ampliarse a un único homomorfismo
![]() de G en
de G en ![]() .
.
Supongamos que existe un homomorfismo
![]() , cuya restricción a
, cuya restricción a ![]() coincide con
coincide con ![]() .
.
Por la definición 1.3.1 vale:
Definimos la aplicación
![]() como la única aplicación lineal que satisface (12) y (13). Como caso particular de (13) tenemos:
como la única aplicación lineal que satisface (12) y (13). Como caso particular de (13) tenemos:
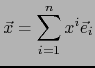 con
con

Resta comprobar la regla:
![${\displaystyle \overline{x}= \sum_{H \subset [\![ 1,n ]\!]} x^H \overline{e}_H \,,\;\overline{y}= \sum_{K \subset [\![ 1,n ]\!]} y^K \overline{e}_K }$](img575.png) con
con
De ahí
![${\displaystyle \overline{x} \wedge \overline{y} = \sum_{H \subset [\![ 1,n ]\!] \atop K \subset [\![ 1,n ]\!] } x^H y^K \overline{e}_H \wedge \overline{e}_K }$](img577.png) , luego:
, luego:
![\begin{displaymath}\tilde \lambda \overline{x} \cdot \tilde \lambda \overline{y}...
...ubset [\![ 1,n ]\!] } y^K \tilde \lambda \overline{e}_K \biggr)\end{displaymath}](img579.png)
En este caso
![]() , luego el primer miembro de (17) vale cero. En virtud de la relación (2) el segundo miembro de (17) es:
, luego el primer miembro de (17) vale cero. En virtud de la relación (2) el segundo miembro de (17) es:
Pongamos
![]() donde
donde
![]() , con lo cual el primer miembro de (17) se escribe:
, con lo cual el primer miembro de (17) se escribe: