Siguiente: Casos particulares Arriba: Álgebra de Grassmann asociada Anterior: Relación entre el álgebra

Ley de conmutación

Lema 1.2   Si $K,\, H$ son partes ajenas de $[\![ 1,n ]\!]$, vale:

$$\fbox{${\displaystyle {\displaystyle \rho_{H,K} \, \rho_{K,H}= (-1)^{\vert K\vert\cdot \vert H\vert}} }$}$$

Demostración
Sean $H,\,K$ partes ajenas de $[\![ 1,n ]\!]$. Sea $\nu_1$ el número de pares $(i,j)$ con $i\in H,\, j\in K$ tales que $i<j$. Sea $\nu_2$ el número de pares $(i,j)$ con $i\in H,\, j\in K$ tales que $i>j$. Por ser $H,\,K$ ajenos $\nu_1 +\nu_2$ es el número total de pares $(i,j)$ tales que $i\in H,\, j\in K$ o sea la cardinalidad $\vert H\vert \cdot \vert K\vert$ del producto cartesiano $H\times K$. Así pues:

$$\rho_{H,K}\cdot \rho_{K,H}=(-1)^{\nu_1} (-1)^{\nu_2} = (-1)^{\nu_1 + \nu_2} =(-1)^{\vert H\vert \cdot \vert K\vert}$$

$\quad\Box$

Teorema 1.5   Si $\overline{x} \in \mbox{\sf G}^{(p)} \; \mbox{e}\; \overline{y} \in \mbox{\sf G}^{(q)}$ vale:

$$\fbox{${\displaystyle {\displaystyle \overline{y}\wedge \over... ...x{: {\sc Ley de Conmutaci\'on}\index{Ley de Conmutaci\'on}} }$}$$

Demostración
Escribamos: 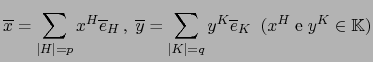${\displaystyle \overline{x} = \sum_{\vert H\vert=p} x^H \overline{e}_H \,,\; \o... ...t K\vert=q} y^K \overline{e}_K \;\; (x^H \; \mbox{e}\; y^K \in {{\mathbb{K}}})}$. De ahí :

$$\overline{x} \wedge \overline{y} = \sum_{\vert H\vert=p \atop \vert K\vert=q} x^H y^K \, \overline{e}_H \wedge \overline{e}_K$$ (16)

$$\overline{y} \wedge \overline{x} = \sum_{\vert H\vert=p \atop \vert K\vert=q} x^H y^K \, \overline{e}_K \wedge \overline{e}_H$$ (17)

En vista de (16) y (17) el teorema estará probado si mostramos:

$$\overline{e}_K \wedge \overline{e}_H = (-1)^{pq}\, \overline{e}_H \wedge \overline{e}_K$$ (18)

siempre que $\vert H\vert=p$ y $\vert K\vert=q$. Ahora bien, por la tabla de multiplicación:

$$\overline{e}_H \wedge \overline{e}_K = \rho_{H,K} \, \overline{e}_{H \cup K} \quad \mbox{y}$$ (19)

$$\overline{e}_K \wedge \overline{e}_H = \rho_{K,H} \, \overline{e}_{H \cup K}$$ (20)

Si $H \cap K \ne \emptyset$, los segundos miembros tanto de (19) como de (20) son cero, luego (18) es cierto (con ambos miembros nulos).

Si $H \cap K = \emptyset$, tenemos por el lema 1.1.2: $\rho_{K,H}= (-1)^{pq} \rho_{H,K}$ y de nuevo (18) es cierto. $\quad\Box$

Siguiente: Casos particulares Arriba: Álgebra de Grassmann asociada Anterior: Relación entre el álgebra