




Siguiente: Álgebra exterior sobre un
Arriba: Ampliación exterior de una
Anterior: Ampliación exterior de una
Demostración
Designemos por
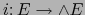 y
y
 las inyecciones canónicas. Consideramos la aplicación lineal ``diagonal''
las inyecciones canónicas. Consideramos la aplicación lineal ``diagonal''
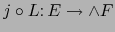 . Se verifica
. Se verifica
 :
:
Así pues,  es una aplicación lineal alternante del espacio vectorial
es una aplicación lineal alternante del espacio vectorial  en el álgebra
en el álgebra 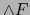 . Por la propiedad universal de la terna
. Por la propiedad universal de la terna
 existe un único homomorfismo
existe un único homomorfismo 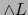 del álgebra
del álgebra 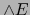 en el álgebra
en el álgebra 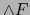 tal que:
tal que:
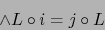 |
(1) |
Ahora bien, la condición (1) significa:
o, en definitiva:
La relación (1) equivale, pues, a decir que el homomorfismo 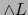 es una ampliación de la aplicación lineal
es una ampliación de la aplicación lineal  .
.

Demostración
- La aplicación
 es un homomorfismo del álgebra
es un homomorfismo del álgebra 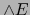 en sí y amplía la aplicación lineal
en sí y amplía la aplicación lineal 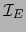 de
de  en
en  . Por la unicidad en el teorema 1.4.1 dicho homomorfismo
. Por la unicidad en el teorema 1.4.1 dicho homomorfismo
 es la ampliación exterior de
es la ampliación exterior de 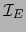 , o sea, efectivamente:
, o sea, efectivamente:
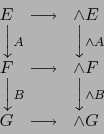
- Observamos que los siguientes diagramas conmutan:
La aplicación
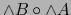 de
de 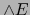 en
en  es un homomorfismo del álgebra
es un homomorfismo del álgebra 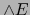 en el álgebra
en el álgebra  . Dicho homomorfismo amplía la aplicación lineal
. Dicho homomorfismo amplía la aplicación lineal 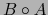 del espacio vectorial
del espacio vectorial  en el espacio vectorial
en el espacio vectorial 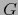 . Por la unicidad en el teorema 1.4.1 el homomorfismo
. Por la unicidad en el teorema 1.4.1 el homomorfismo
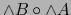 es la ampliación exterior de
es la ampliación exterior de 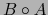 , o sea
, o sea

A título auxiliar vamos a recordar dos resultados de álgebra lineal.
Demostración
- Supongamos que existe una aplicación lineal
 tal que:
tal que:
 |
(2) |
Sean
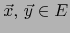 tales que:
tales que:
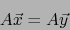 |
(3) |
Aplicando 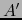 a los dos miembros de (3) obtenemos:
a los dos miembros de (3) obtenemos:
o sea, por (2),
 . Por tanto la aplicación lineal
. Por tanto la aplicación lineal 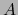 es inyectiva.
es inyectiva.
- Recíprocamente supongamos
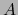 inyectiva. Podemos considerar
inyectiva. Podemos considerar 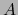 como un isomorfismo lineal del espacio vectorial
como un isomorfismo lineal del espacio vectorial  sobre el subespacio
sobre el subespacio 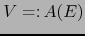 de
de  . Sea
. Sea
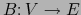 el isomorfismo lineal inverso de éste. Sea
el isomorfismo lineal inverso de éste. Sea 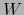 un subespacio vectorial de
un subespacio vectorial de  complementario al subespacio
complementario al subespacio  , es decir
, es decir
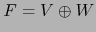 . Tal subespacio
. Tal subespacio 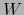 siempre existe. (Si
siempre existe. (Si  es de dimensión finita esto se demuestra simplemente completando una base
es de dimensión finita esto se demuestra simplemente completando una base
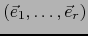 de
de  a una base
a una base
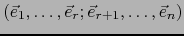 de
de  y tomando por
y tomando por  el subespacio de
el subespacio de  engendrado por
engendrado por
 ).
).
Definamos la aplicación lineal  de
de  en
en  como la única que satisface:
como la única que satisface:
Vale patentemente:
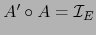 .
.

Demostración
- Supongamos que existe una aplicación lineal
 tal que
tal que
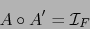 |
(4) |
Sea 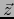 un vector arbitrario de
un vector arbitrario de  . Para el vector
. Para el vector
 de
de  vale por (4):
vale por (4):
Así pues la aplicación lineal 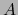 es superyectiva.
es superyectiva.
- Recíprocamente supongamos que
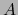 es superyectiva. Sea
es superyectiva. Sea  un subespacio de
un subespacio de  complementario al subespacio
complementario al subespacio
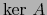 (núcleo de
(núcleo de 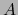 ), o sea
), o sea
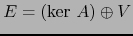 . Afirmamos que la restricción
. Afirmamos que la restricción  de la aplicación
de la aplicación 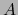 al subespacio
al subespacio  es un isomorfismo lineal de
es un isomorfismo lineal de  sobre
sobre  .
.
En efecto, sea 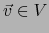 tal que
tal que 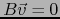 , es decir
, es decir 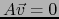 . Se sigue que
. Se sigue que
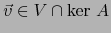 , es decir
, es decir
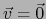 . Esto prueba que la aplicación lineal
. Esto prueba que la aplicación lineal
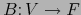 es inyectiva. Mostremos que es también superyectiva. Sea
es inyectiva. Mostremos que es también superyectiva. Sea 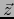 un vector arbitrario de
un vector arbitrario de  . Por ser
. Por ser 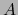 superyectiva existe un vector
superyectiva existe un vector
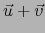 de
de  , donde
, donde
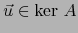 ,
, 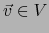 tal que
tal que
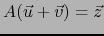 . Esto equivale a
. Esto equivale a
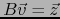 .
.  es pues efectivamente superyectiva y, en definitiva, un isomorfismo lineal de
es pues efectivamente superyectiva y, en definitiva, un isomorfismo lineal de  sobre
sobre  .
.
Sea
 la aplicación
la aplicación
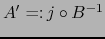 donde
donde
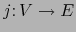 es la inyección canónica. Patentemente:
es la inyección canónica. Patentemente:

Volvamos al álgebra exterior.
Teorema 4.5
Sean 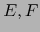 espacios vectoriales de dimensiones finitas.
espacios vectoriales de dimensiones finitas.
- Si
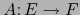 es una aplicación lineal inyectiva, la aplicación
es una aplicación lineal inyectiva, la aplicación 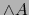 es un homomorfismo inyectivo (``monomorfismo'') del álgebra
es un homomorfismo inyectivo (``monomorfismo'') del álgebra 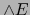 en el álgebra
en el álgebra 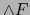 .
.
- Si
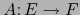 es una aplicación lineal superyectiva, la aplicación
es una aplicación lineal superyectiva, la aplicación 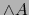 es un homomorfismo superyectivo (``epimorfismo'') del álgebra
es un homomorfismo superyectivo (``epimorfismo'') del álgebra 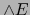 sobre el álgebra
sobre el álgebra 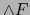 .
.
Demostración
- Supongamos que
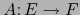 es una aplicación lineal inyectiva. Por el teorema 1.4.3 existe una aplicación lineal
es una aplicación lineal inyectiva. Por el teorema 1.4.3 existe una aplicación lineal
 tal que
tal que
 |
(5) |
Tomando las ampliaciones exteriores de ambos miembros de (5) y aplicando el teorema 1.4.2 conseguimos:
De nuevo del teorema 1.4.3 se sigue que 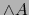 es una aplicación inyectiva.
es una aplicación inyectiva.
- Supongamos que
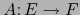 es una aplicación lineal superyectiva. Por el teorema 1.4.3 existe una aplicación lineal
es una aplicación lineal superyectiva. Por el teorema 1.4.3 existe una aplicación lineal
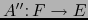 tal que:
tal que:
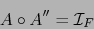 |
(6) |
De (6) se obtiene por el teorema 1.4.2:
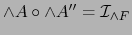 .
De ahí se sigue de nuevo por el teorema 1.4.3 que
.
De ahí se sigue de nuevo por el teorema 1.4.3 que 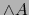 es una aplicación superyectiva.
es una aplicación superyectiva.

Nota
El recíproco del teorema 1.4.5 se demostrará más adelante como teorema 1.4.10.
Demostración
Del teorema 1.4.5 se desprende sin más que 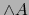 es un isomorfismo del álgebra
es un isomorfismo del álgebra 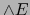 sobre el álgebra
sobre el álgebra  . Se verifican las relaciones:
. Se verifican las relaciones:
Tomando las ampliaciones exteriores de ambos miembros de estas fórmulas obtenemos por el teorema 1.4.2:
De ahí se ve de nuevo que 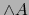 es un isomorfismo del álgebra
es un isomorfismo del álgebra 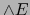 sobre el álgebra
sobre el álgebra  y también que
y también que
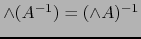 .
.

Definición 4.1
Sean 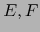 espacios vectoriales de dimensiones finitas y
espacios vectoriales de dimensiones finitas y 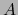 una aplicación lineal
una aplicación lineal 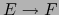 .
.
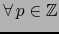 se designa por
se designa por
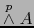 y se llama
y se llama  -ésima POTENCIA EXTERIOR DE LA APLICACIÓN LINEAL
-ésima POTENCIA EXTERIOR DE LA APLICACIÓN LINEAL 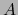 a la restricción del homomorfismo
a la restricción del homomorfismo 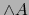 al subespacio
al subespacio
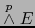 de
de 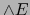 .
.
Notamos que:
Supongamos
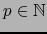 . Ya que
. Ya que
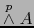 es la restricción a
es la restricción a
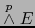 del homomorfismo
del homomorfismo 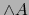 , vale
, vale
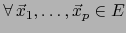 :
:
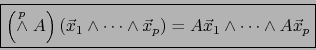 |
(7) |
El segundo miembro de esta fórmula es un elemento del espacio vectorial
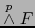 . Puesto que todo elemento de
. Puesto que todo elemento de
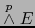 es una suma de elementos descomponibles, se sigue de la fórmula (7) que
es una suma de elementos descomponibles, se sigue de la fórmula (7) que
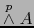 aplica el espacio vectorial
aplica el espacio vectorial
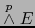 en el subespacio
en el subespacio
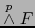 del álgebra
del álgebra
 . Cambiando ligeramente la notación consideraremos pues de aquí en adelante
. Cambiando ligeramente la notación consideraremos pues de aquí en adelante
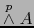 como una aplicación lineal del espacio vectorial
como una aplicación lineal del espacio vectorial
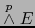 en el espacio vectorial
en el espacio vectorial
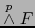 .
.
Observación
Si
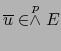 ,
,
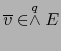 y
y
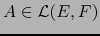 , se verifica:
, se verifica:
En efecto, todas las potencias exteriores de 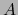 que figuran en esta fórmula son restricciones de la ampliación exterior
que figuran en esta fórmula son restricciones de la ampliación exterior 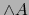 y ésta es un homomorfismo de álgebras.
y ésta es un homomorfismo de álgebras.
Teorema 4.6
Las siguientes aseveraciones son ciertas:
- Si
 es un espacio vectorial de dimensión finita, vale
es un espacio vectorial de dimensión finita, vale 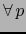 :
:
- Si
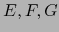 son espacios vectoriales de dimensiones finitas y
son espacios vectoriales de dimensiones finitas y
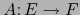 ,
,
 son aplicaciones lineales vale:
son aplicaciones lineales vale:
Demostración
- Puesto que
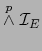 es la restricción de
es la restricción de
 al espacio vectorial
al espacio vectorial
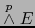 , vale en virtud del teorema 1.4.2
, vale en virtud del teorema 1.4.2
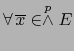 :
:
probando el enunciado a.
- Puesto que
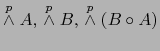 son restricciones de las aplicaciones
son restricciones de las aplicaciones
 a sendos espacios vectoriales
a sendos espacios vectoriales
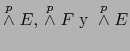 , vale en virtud del teorema 1.4.2
, vale en virtud del teorema 1.4.2
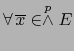 :
:
probando el enunciado b.

Teorema 4.7
Sean 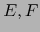 espacios vectoriales de dimensiones finitas:
espacios vectoriales de dimensiones finitas:
- Si
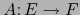 es una aplicación lineal inyectiva entonces también
es una aplicación lineal inyectiva entonces también
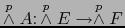 es una aplicación lineal inyectiva.
es una aplicación lineal inyectiva.
- Si
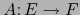 es una aplicación lineal superyectiva entonces también
es una aplicación lineal superyectiva entonces también
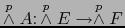 es una aplicación lineal superyectiva.
es una aplicación lineal superyectiva.
Demostración
- Supongamos la aplicación
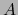 inyectiva. Por el teorema 1.4.5 la aplicación
inyectiva. Por el teorema 1.4.5 la aplicación 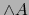 es también inyectiva. Luego
es también inyectiva. Luego
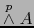 , restricción de ésta es también inyectiva.
, restricción de ésta es también inyectiva.
- Supongamos
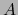 superyectiva. Por el teorema 1.4.5 también
superyectiva. Por el teorema 1.4.5 también 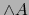 es superyectiva. Luego si
es superyectiva. Luego si 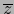 es un elemento arbitrario de
es un elemento arbitrario de
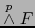 existe
existe
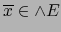 tal que
tal que
 |
(8) |
Podemos escribir de manera única:
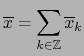 con
con
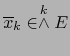 . De ahí
. De ahí
 con
con
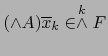 . Comparando con (8), vemos que
. Comparando con (8), vemos que
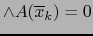 si
si 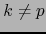 y (8) se reduce a:
y (8) se reduce a:
probando el enunciado b.

Nota
El recíproco del teorema 1.4.7 se probará más adelante como teorema 1.4.10.
Demostración
Las dos partes del teorema 1.4.7 hacen patente que
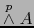 es un isomorfismo lineal de
es un isomorfismo lineal de
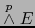 sobre
sobre
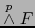 . Rigen las relaciones:
. Rigen las relaciones:
Al tomar las  -ésimas potencias exteriores de ambos miembros de (9) y (10) se obtiene en virtud del teorema 1.4.6:
-ésimas potencias exteriores de ambos miembros de (9) y (10) se obtiene en virtud del teorema 1.4.6:
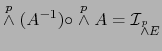 |
|
|
(11) |
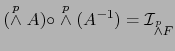 |
|
|
(12) |
Estas relaciones prueban otras vez que
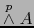 es un isomorfismo de
es un isomorfismo de
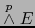 sobre
sobre
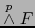 y además que
y además que
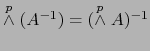 .
.

Demostración
- Supongamos
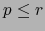 .
.
Sean
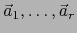 vectores de
vectores de  tales que la familia
tales que la familia
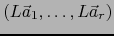 constituye una base del subespacio
constituye una base del subespacio 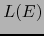 de
de  . La subfamilia
. La subfamilia
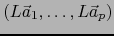 de dicha base es linealmente independiente. De ahí por el teorema 1.3.4:
de dicha base es linealmente independiente. De ahí por el teorema 1.3.4:
Así pues
 .
.
- Supongamos
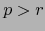 .
.
Para todo  -uplo
-uplo
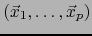 de vectores de
de vectores de  , el
, el  -uplo
-uplo
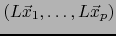 de vectores de
de vectores de 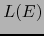 es linealmente dependiente, luego, por el teorema 1.3.4:
es linealmente dependiente, luego, por el teorema 1.3.4:
Esta relación prueba que
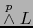 se anula sobre todos los elementos descomponibles de
se anula sobre todos los elementos descomponibles de
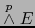 . Ya que éstos engendran el espacio vectorial
. Ya que éstos engendran el espacio vectorial
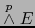 , vale
, vale
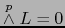 .
.






Siguiente: Álgebra exterior sobre un
Arriba: Ampliación exterior de una
Anterior: Ampliación exterior de una
Guillermo M. Luna
2009-06-14

![]() de
de ![]() en
en ![]() como la única que satisface:
como la única que satisface:

![]() tal que
tal que ![]() , es decir
, es decir ![]() . Se sigue que
. Se sigue que
![]() , es decir
, es decir
![]() . Esto prueba que la aplicación lineal
. Esto prueba que la aplicación lineal
![]() es inyectiva. Mostremos que es también superyectiva. Sea
es inyectiva. Mostremos que es también superyectiva. Sea ![]() un vector arbitrario de
un vector arbitrario de ![]() . Por ser
. Por ser ![]() superyectiva existe un vector
superyectiva existe un vector
![]() de
de ![]() , donde
, donde
![]() ,
, ![]() tal que
tal que
![]() . Esto equivale a
. Esto equivale a
![]() .
. ![]() es pues efectivamente superyectiva y, en definitiva, un isomorfismo lineal de
es pues efectivamente superyectiva y, en definitiva, un isomorfismo lineal de ![]() sobre
sobre ![]() .
.
![]() la aplicación
la aplicación
![]() donde
donde
![]() es la inyección canónica. Patentemente:
es la inyección canónica. Patentemente:
![]() es un isomorfismo del álgebra
es un isomorfismo del álgebra ![]() sobre el álgebra
sobre el álgebra ![]() . Se verifican las relaciones:
. Se verifican las relaciones:
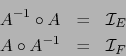
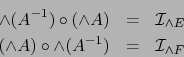
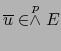 ,
,
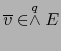 y
y
![]() , se verifica:
, se verifica:
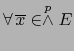 :
:
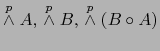 son restricciones de las aplicaciones
son restricciones de las aplicaciones
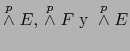 , vale en virtud del teorema 1.4.2
, vale en virtud del teorema 1.4.2
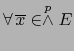 :
:

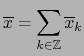 con
con
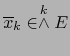 . De ahí
. De ahí
 con
con
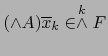 . Comparando con (8), vemos que
. Comparando con (8), vemos que

![]() es un isomorfismo lineal de
es un isomorfismo lineal de
![]() sobre
sobre
![]() . Rigen las relaciones:
. Rigen las relaciones:
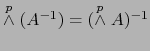 .
.
![]() vectores de
vectores de ![]() tales que la familia
tales que la familia
![]() constituye una base del subespacio
constituye una base del subespacio ![]() de
de ![]() . La subfamilia
. La subfamilia
![]() de dicha base es linealmente independiente. De ahí por el teorema 1.3.4:
de dicha base es linealmente independiente. De ahí por el teorema 1.3.4:
 .
.
![]() -uplo
-uplo
![]() de vectores de
de vectores de ![]() , el
, el ![]() -uplo
-uplo
![]() de vectores de
de vectores de ![]() es linealmente dependiente, luego, por el teorema 1.3.4:
es linealmente dependiente, luego, por el teorema 1.3.4: