




Siguiente: Teoría de determinantes
Arriba: Ampliación exterior de una
Anterior: Determinantes
Sean  un espacio vectorial de dimensión finita y
un espacio vectorial de dimensión finita y  un subespacio de
un subespacio de  . Designamos por
. Designamos por
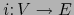 la inyección canónica. Por el teorema 1.4.5 la aplicación
la inyección canónica. Por el teorema 1.4.5 la aplicación
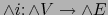 es un homomorfismo inyectivo del álgebra
es un homomorfismo inyectivo del álgebra  en el álgebra
en el álgebra 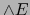 . Permite identificar
. Permite identificar  , el álgebra exterior sobre
, el álgebra exterior sobre  con su imagen
con su imagen
 , subálgebra del álgebra exterior
, subálgebra del álgebra exterior 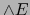 sobre
sobre  .
.
Elementos
 se identificarán con sendos elementos
se identificarán con sendos elementos
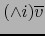 ,
,
 de
de 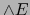 y
el producto exterior
y
el producto exterior
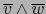 con:
con:
Asimismo por el teorema 1.4.7
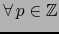 el subespacio
el subespacio
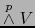 , espacio vectorial de los
, espacio vectorial de los  -vectores sobre
-vectores sobre  se identificará con
se identificará con
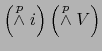 subespacio vectorial de
subespacio vectorial de
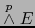 . Ya que el espacio
. Ya que el espacio
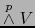 está engendrado linealmente por los productos
está engendrado linealmente por los productos
 con
con
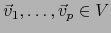 , el espacio vectorial
, el espacio vectorial
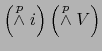 identificado con éste está engendrado por los productos
identificado con éste está engendrado por los productos
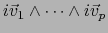 (
(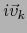 es el mismo vector que
es el mismo vector que 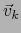 pero considerado como elemento de
pero considerado como elemento de  ).
).
Teorema 4.9
Sean 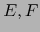 espacios vectoriales de dimensiones finitas y
espacios vectoriales de dimensiones finitas y
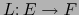 una aplicación lineal de rango
una aplicación lineal de rango 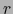 :
:
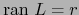 . Vale:
. Vale:
Demostración
Pongamos
 .
.  es un subespacio de
es un subespacio de  de dimensión
de dimensión 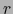 . Sean
. Sean
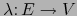 la aplicación lineal definida por
la aplicación lineal definida por
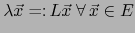 y
y
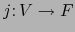 la inyección canónica. Se verifica pues
la inyección canónica. Se verifica pues
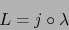 |
(13) |
- Por el teorema 1.4.2 y la relación (13) el homomorfismo
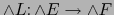 puede representarse por:
puede representarse por:
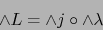 |
(14) |
Puesto que
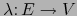 es una aplicación lineal superyectiva, por el teorema 1.4.5
es una aplicación lineal superyectiva, por el teorema 1.4.5
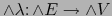 es también una aplicación superyectiva, luego
es también una aplicación superyectiva, luego
Por el teorema 1.4.5  es inyectiva, luego por (14):
es inyectiva, luego por (14):
como afirmamos.
-
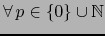 vale por el teorema 1.4.6:
vale por el teorema 1.4.6:
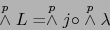 |
(15) |
y por el teorema 1.4.7:
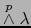 es una aplicación lineal superyectiva de
es una aplicación lineal superyectiva de
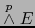 sobre
sobre
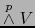 mientras que
mientras que
 es una aplicación lineal inyectiva de
es una aplicación lineal inyectiva de
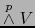 en
en
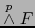 , luego por (15):
, luego por (15):

Observación
El teorema 1.4.9 es más preciso que el teorema 1.4.8 y permite
recobrar éste. En efecto, sean  ,
,  espacios vectoriales de dimensiones finitas y
espacios vectoriales de dimensiones finitas y
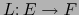 una aplicación lineal de rango
una aplicación lineal de rango 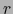 . Sea
. Sea
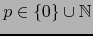 . Por el teorema 1.4.9 si
. Por el teorema 1.4.9 si
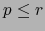 , se cumple
, se cumple
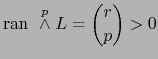 , luego
, luego
 y si
y si 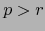 :
:
 , luego
, luego
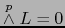 .
.
Mediante el teorema 1.4.9 podemos también demostrar fácilmente los recíprocos de los teoremas 1.4.5 y 1.4.7.
Teorema 4.10
Sean 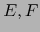 espacios vectoriales de sendas dimensiones finitas
espacios vectoriales de sendas dimensiones finitas 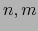 . Sea
. Sea
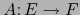 una aplicación lineal.
una aplicación lineal.
- Si el homomorfismo
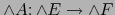 es inyectivo, A es una aplicación lineal inyectiva.
es inyectivo, A es una aplicación lineal inyectiva.
- Si el homomorfismo
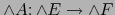 es superyectivo, A es una aplicación lineal superyectiva.
es superyectivo, A es una aplicación lineal superyectiva.
- Si para algún
![$p \in [\![ 0,n ]\!]$](img156.png) ,
,
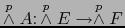 es una aplicación lineal inyectiva, A es una aplicación lineal inyectiva.
es una aplicación lineal inyectiva, A es una aplicación lineal inyectiva.
- Si para algún
![$p \in [\![ 0,m ]\!]$](img840.png) ,
,
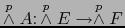 es una aplicación lineal superyectiva, A es una aplicación lineal superyectiva.
es una aplicación lineal superyectiva, A es una aplicación lineal superyectiva.
Demostración
Sea
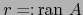 .
.
- Supongamos que
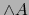 es inyectiva. Luego:
es inyectiva. Luego:
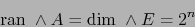 |
(16) |
Pero por el teorema 1.4.9 también:
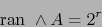 |
(17) |
Al cotejar (16) con (17) obtenemos  . Así pues
. Así pues 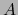 es inyectiva.
es inyectiva.
- Supongamos que
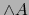 es superyectiva. Luego:
es superyectiva. Luego:
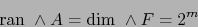 |
(18) |
Por el teorema 1.4.9 tenemos también
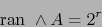 |
(19) |
Al cotejar (18) con (19) obtenemos 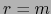 . Así pues,
. Así pues, 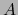 es superyectiva.
es superyectiva.
- Supongamos que para cierto
![$p \in [\![ 0,n ]\!]$](img156.png) :
:
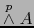 es una aplicación lineal inyectiva, o sea:
es una aplicación lineal inyectiva, o sea:
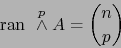 |
(20) |
Pero por el teorema 1.4.9 vale también:
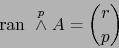 |
(21) |
Comparando (20) con (21) obtenemos  , luego
, luego 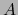 es una aplicación lineal inyectiva.
es una aplicación lineal inyectiva.
- Supongamos que para cierto
![$p \in [\![ 0,m ]\!]$](img840.png) la aplicación lineal
la aplicación lineal
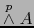 es una aplicación superyectiva
es una aplicación superyectiva
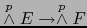 . Vale pues
. Vale pues
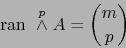 |
(22) |
Por el teorema 1.4.9 tenemos también:
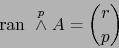 |
(23) |
De (22) y (23) se sigue 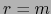 . Por tanto la aplicación lineal
. Por tanto la aplicación lineal 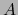 es superyectiva.
es superyectiva.






Siguiente: Teoría de determinantes
Arriba: Ampliación exterior de una
Anterior: Determinantes
Guillermo M. Luna
2009-06-14
![]() un espacio vectorial de dimensión finita y
un espacio vectorial de dimensión finita y ![]() un subespacio de
un subespacio de ![]() . Designamos por
. Designamos por
![]() la inyección canónica. Por el teorema 1.4.5 la aplicación
la inyección canónica. Por el teorema 1.4.5 la aplicación
![]() es un homomorfismo inyectivo del álgebra
es un homomorfismo inyectivo del álgebra ![]() en el álgebra
en el álgebra ![]() . Permite identificar
. Permite identificar ![]() , el álgebra exterior sobre
, el álgebra exterior sobre ![]() con su imagen
con su imagen
![]() , subálgebra del álgebra exterior
, subálgebra del álgebra exterior ![]() sobre
sobre ![]() .
.
![]() se identificarán con sendos elementos
se identificarán con sendos elementos
![]() ,
,
![]() de
de ![]() y
el producto exterior
y
el producto exterior
![]() con:
con:
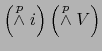 subespacio vectorial de
subespacio vectorial de
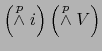 identificado con éste está engendrado por los productos
identificado con éste está engendrado por los productos
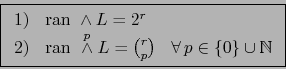
![]() .
. ![]() es un subespacio de
es un subespacio de ![]() de dimensión
de dimensión ![]() . Sean
. Sean
![]() la aplicación lineal definida por
la aplicación lineal definida por
![]() y
y
![]() la inyección canónica. Se verifica pues
la inyección canónica. Se verifica pues
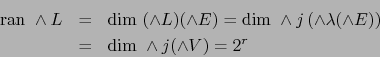
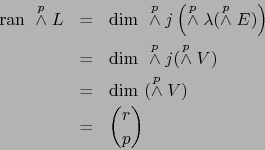
![]() ,
, ![]() espacios vectoriales de dimensiones finitas y
espacios vectoriales de dimensiones finitas y
![]() una aplicación lineal de rango
una aplicación lineal de rango ![]() . Sea
. Sea
![]() . Por el teorema 1.4.9 si
. Por el teorema 1.4.9 si
![]() , se cumple
, se cumple
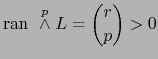 , luego
, luego
 y si
y si ![]() :
:
 , luego
, luego
![]() .
.
![]() .
.