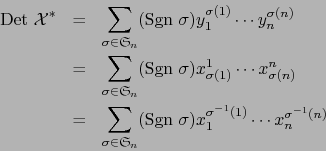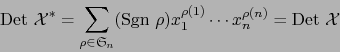Siguiente: Determinante de un -uplo
Arriba: Ampliación exterior de una
Anterior: Álgebra exterior sobre un
El álgebra exterior, como pronto nos convenceremos, es el marco ideal para tratar la teoría de determinantes y éstos desempeñan un papel importante en ella. Vamos pues aquí a exponer la teoría de determinantes sin suponer ningún conocimiento previo de ellos.
Recordamos:
Definición 4.2
Sean  un espacio vectorial sobre un cuerpo conmutativo
un espacio vectorial sobre un cuerpo conmutativo  y
y
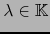 . La aplicación
. La aplicación
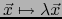 de
de  en
en  se llama HOMOTECIA DE RAZÓN . Es un endomorfismo lineal de
se llama HOMOTECIA DE RAZÓN . Es un endomorfismo lineal de  (es decir una aplicación lineal de
(es decir una aplicación lineal de  en
en  ).
).
También recordamos:
Teorema 4.11
Todo endomorfismo lineal de un espacio vectorial  de dimensión uno es una homotecia de
de dimensión uno es una homotecia de  .
.
Demostración
Sea  un espacio vectorial de dimensión
un espacio vectorial de dimensión  sobre un cuerpo conmutativo
sobre un cuerpo conmutativo  . Sea
. Sea 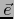 un vector arbitrario no nulo de
un vector arbitrario no nulo de  . La familia reducida al elemento
. La familia reducida al elemento 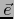 es una base de
es una base de  . Sea
. Sea
 un endomorfismo lineal de
un endomorfismo lineal de  . Puesto que todo elemento de
. Puesto que todo elemento de  se expresa únicamente como un múltiplo escalar de
se expresa únicamente como un múltiplo escalar de 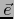 , existe un único
, existe un único
 tal que:
tal que:
Un vector arbitrario 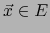 se escribe únicamente en la forma:
se escribe únicamente en la forma:
Vale pues:
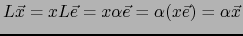 .
.  es pues
la homotecia de
es pues
la homotecia de  de razón
de razón 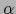 .
.

Definición 4.3
Sea  un espacio vectorial de dimensión finita
un espacio vectorial de dimensión finita  sobre un cuerpo conmutativo
sobre un cuerpo conmutativo  . Puesto que
. Puesto que
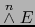 es un espacio vectorial de dimensión 1, por el teorema 1.4.11 el endomorfismo lineal
es un espacio vectorial de dimensión 1, por el teorema 1.4.11 el endomorfismo lineal
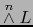 del espacio vectorial
del espacio vectorial
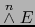 es una homotecia de dicho espacio vectorial. La razón de dicha homotecia se llama el DETERMINANTE DEL ENDOMORFISMO
es una homotecia de dicho espacio vectorial. La razón de dicha homotecia se llama el DETERMINANTE DEL ENDOMORFISMO  y se designa por
y se designa por
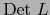 .
.
En otras palabras,
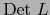 es el elemento del cuerpo
es el elemento del cuerpo  que satisface:
que satisface:
Demostración
- La fórmula
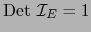 sigue sin más de la relación
sigue sin más de la relación
probada en el teorema 1.4.6.
- Sean
 endomorfismos lineales de
endomorfismos lineales de  . Usando el teorema 1.4.6 obtenemos:
. Usando el teorema 1.4.6 obtenemos:
de ahí que:
- Sea
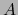 un endomorfismo lineal de
un endomorfismo lineal de  . La relación
. La relación
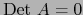 equivale a:
equivale a:
y ésta, a su vez, en virtud del teorema 1.4.8, a:
- Sea
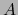 un automorfismo lineal de
un automorfismo lineal de  y
y 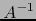 el correspondiente
automorfismo inverso. Se cumple:
el correspondiente
automorfismo inverso. Se cumple:
Tomando los determinantes de ambos miembros obtenemos en virtud de los incisos a. y b.:

Observación
El conjunto de todos los automorfismos lineales de  provisto de la ley de composición
provisto de la ley de composición
constituye un grupo, el GRUPO LINEAL de  .
.
Del teorema 1.4.12 se desprende sin más:
Si E es un espacio vectorial de dimensión finita sobre un cuerpo conmutativo  la aplicación
la aplicación
del grupo lineal E en el grupo ``multiplicativo''
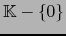 (es decir, del conjunto
(es decir, del conjunto
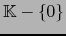 provisto de la restricción de la multiplicación en
provisto de la restricción de la multiplicación en  ) es un homomorfismo de grupos.
) es un homomorfismo de grupos.
Demostración
Sea
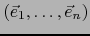 una base arbitraria. Decir que la matriz
una base arbitraria. Decir que la matriz
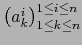 de tipo
de tipo 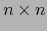 , de elementos en
, de elementos en  es la matriz del endomorfismo
es la matriz del endomorfismo 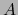 con respecto a dicha base, es decir que valen las relaciones:
con respecto a dicha base, es decir que valen las relaciones:
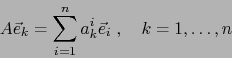 |
(24) |
Usando (24), obtenemos:
Los términos en el último miembro de (25) con
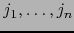 no todos distintos valen cero. Al omitir dichos términos quedan aquellos con
no todos distintos valen cero. Al omitir dichos términos quedan aquellos con
 para alguna permutación
para alguna permutación
 . De (25) obtenemos pues:
. De (25) obtenemos pues:
y, puesto que
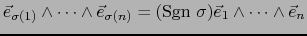 , en definitiva:
, en definitiva:
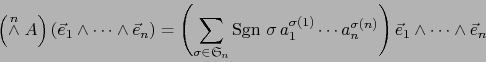 |
(26) |
Pero también:
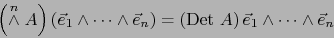 |
(27) |
Al comparar (26) y (27) conseguimos finalmente:

Definición 4.4
Sea
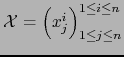 una matriz de tipo
una matriz de tipo 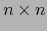 de elementos en un cuerpo conmutativo
de elementos en un cuerpo conmutativo  . El escalar
se llama el DETERMINANTE DE LA MATRIZ
. El escalar
se llama el DETERMINANTE DE LA MATRIZ 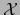 . Se escribe:
. Se escribe:
Debido a esta definición, el teorema 1.4.13 puede enunciarse:
El determinante de un endomorfismo de un espacio vectorial  de dimensión finita es igual al determinante de la matriz de dicho endomorfismo con respecto a una base arbitraria de
de dimensión finita es igual al determinante de la matriz de dicho endomorfismo con respecto a una base arbitraria de  .
.
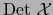 suele representarse también por el símbolo
suele representarse también por el símbolo
Designaremos por
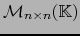 el álgebra de todas las matrices de tipo
el álgebra de todas las matrices de tipo 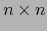 , de elementos en
, de elementos en  . A todo endomorfismo
lineal
. A todo endomorfismo
lineal 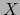 del espacio vectorial
del espacio vectorial
 hagámosle corresponder su matriz
hagámosle corresponder su matriz ![$[ X]$](img904.png) con respecto a la base natural de
con respecto a la base natural de
 .
.
La aplicación ![$X \mapsto [X]$](img905.png) es un isomorfismo del álgebra
es un isomorfismo del álgebra
 de todos los endomorfismos de
de todos los endomorfismos de
 sobre el álgebra
sobre el álgebra
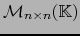 . En particular tenemos:
. En particular tenemos:
donde 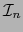 es la ``matriz unidad de orden
es la ``matriz unidad de orden  '' o sea:
'' o sea:
Un endomorfismo 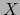 de
de
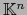 es un automorfismo lineal de
es un automorfismo lineal de
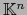 si y sólo si la matriz
si y sólo si la matriz ![$[ X]$](img904.png) es inversible y entonces
es inversible y entonces
![$[X^{-1}] = [X]^{-1}$](img911.png) la inversa de la matriz
la inversa de la matriz ![$[ X]$](img904.png) . Además,
. Además,
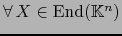 vale:
vale:
De estos hechos y del teorema 1.4.12, se desprenden inmediatamente los siguientes resultados sobre los determinantes de las matrices 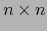 .
.
Claramente
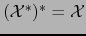 .
.
Demostración
Sean
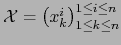 y
y
 donde
donde
![$y_i^k = x_k^i \; \forall \, i \in [\![ 1,n ]\!] $](img929.png)
![$\forall \, k \in [\![ 1,n ]\!]$](img301.png) .
Aprovechando la conmutatividad del cuerpo
.
Aprovechando la conmutatividad del cuerpo  , podemos escribir:
, podemos escribir:
o sea, al poner
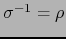 y notando que
y notando que
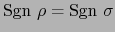 :
:






Siguiente: Determinante de un -uplo
Arriba: Ampliación exterior de una
Anterior: Álgebra exterior sobre un
Guillermo M. Luna
2009-06-14
![]() un espacio vectorial de dimensión
un espacio vectorial de dimensión ![]() sobre un cuerpo conmutativo
sobre un cuerpo conmutativo ![]() . Sea
. Sea ![]() un vector arbitrario no nulo de
un vector arbitrario no nulo de ![]() . La familia reducida al elemento
. La familia reducida al elemento ![]() es una base de
es una base de ![]() . Sea
. Sea
![]() un endomorfismo lineal de
un endomorfismo lineal de ![]() . Puesto que todo elemento de
. Puesto que todo elemento de ![]() se expresa únicamente como un múltiplo escalar de
se expresa únicamente como un múltiplo escalar de ![]() , existe un único
, existe un único
![]() tal que:
tal que:
![]() es el elemento del cuerpo
es el elemento del cuerpo ![]() que satisface:
que satisface:
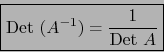

![]() provisto de la ley de composición
provisto de la ley de composición
![]() la aplicación
la aplicación

![]() una base arbitraria. Decir que la matriz
una base arbitraria. Decir que la matriz
![]() de tipo
de tipo ![]() , de elementos en
, de elementos en ![]() es la matriz del endomorfismo
es la matriz del endomorfismo ![]() con respecto a dicha base, es decir que valen las relaciones:
con respecto a dicha base, es decir que valen las relaciones:
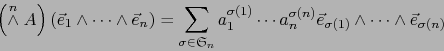
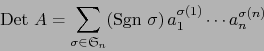
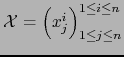 una matriz de tipo
una matriz de tipo 

![]() de dimensión finita es igual al determinante de la matriz de dicho endomorfismo con respecto a una base arbitraria de
de dimensión finita es igual al determinante de la matriz de dicho endomorfismo con respecto a una base arbitraria de ![]() .
.
![]() suele representarse también por el símbolo
suele representarse también por el símbolo
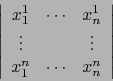
![]() el álgebra de todas las matrices de tipo
el álgebra de todas las matrices de tipo ![]() , de elementos en
, de elementos en ![]() . A todo endomorfismo
lineal
. A todo endomorfismo
lineal ![]() del espacio vectorial
del espacio vectorial
![]() hagámosle corresponder su matriz
hagámosle corresponder su matriz ![]() con respecto a la base natural de
con respecto a la base natural de
![]() .
.
![]() es un isomorfismo del álgebra
es un isomorfismo del álgebra
![]() de todos los endomorfismos de
de todos los endomorfismos de
![]() sobre el álgebra
sobre el álgebra
![]() . En particular tenemos:
. En particular tenemos:
![]() y
y
![]() donde
donde
![]()
![]() .
Aprovechando la conmutatividad del cuerpo
.
Aprovechando la conmutatividad del cuerpo ![]() , podemos escribir:
, podemos escribir: