Siguiente: Menores de una matriz Arriba: Ampliación exterior de una Anterior: Determinante de un -uplo

Orientación de un espacio vectorial real de dimensión finita

Sea $E$ un espacio vectorial de dimensión finita sobre el cuerpo ${\mathbb{R}}$ de los números reales. El concepto de ``orientación'' de $E$ es bien intuitivo en el caso $n=1$. Por esta razón, aunque no haya para ello necesidad lógica, consideraremos primero este caso particular.

1. Sea $E$ un espacio vectorial real de dimensión 1. En el conjunto $E- \{ 0 \}$ de los vectores no nulos de $E$, introducimos una relación ``$\sim$'' por el convenio:
   
   $$\fbox{${\displaystyle \vec v \sim \vec u \iff \exists\, \alpha >0\;\; \mbox{tal que} \;\; \vec v = \alpha \vec u }$}$$
   
   
   1. La relación $\sim$ es reflexiva pues $\vec u = 1 \cdot \vec u \quad \forall \, \vec u \in E-\{ 0 \}$.
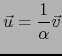   2. La relación $\sim$ es simétrica, pues $\vec u,\, \vec v \in E,\, \vec v = \alpha \vec u$ con $\alpha >0$ implica ${\displaystyle \vec u ={1 \over \alpha} \vec v}$ donde también ${\displaystyle {1 \over \alpha} >0}$.
   3. La relación $\sim$ es transitiva. En efecto, sean $\vec u, \, \vec v,\, \vec w \in E-\{ 0 \}$ tales que $\vec v \sim \vec u$ y $\vec w \sim \vec v$. Rigen unas relaciones: $\vec v = \alpha \vec u$ y $\vec w = \beta \vec v$ con $\alpha >0,\, \beta >0$, de donde $\vec w = \alpha \beta \vec u$. Puesto que $\alpha \beta >0$ se tiene $\vec w \sim \vec u$.
   De (i), (ii), y (iii) se sigue que $\sim$ es una relación de equivalencia en $E- \{ 0 \}$. Fijemos a $\vec{u}_0 \in E-\{ 0 \}$: Todo vector no nulo de $E$ es bien equivalente a $\vec{u}_0$ o bien a $-\vec{u}_0$ y los dos vectores $\vec{u}_0$ y $-\vec{u}_0$ son inequivalentes. Hay, pues, exactamente dos clases de equivalencia para la relación $\sim$, a saber, aquellos del vector $\vec{u}_0$ y del vector $-\vec{u}_0$. Se llaman los dos SENTIDOS DEL ESPACIO VECTORIAL REAL $E$ de dimensión 1.

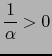   Para no violentar el idioma castellano diremos de dos vectores $\vec u ,\, \vec v \in E-\{ 0 \}$ que SON DEL MISMO SENTIDO o TIENEN EL MISMO SENTIDO en vez de decir que ``están en el mismo sentido''.

2. Pasemos al caso general de ser $E$ un espacio vectorial real de dimensión finita $n$ arbitraria.

   Ya que $\mbox{\rm dim } \stackrel{n}{\wedge} E =1$, podemos aplicarle al espacio vectorial $\stackrel{n}{\wedge} E$ los resultados del inciso a).

   La relación ``$\sim$'' en $\stackrel{n}{\wedge} E -\{ 0 \}$ definida por:
   

   $$\overline{v} \sim \overline{u} \iff \exists\, \alpha >0 \;\; \mbox{tal que} \;\; \overline{v}= \alpha \overline{u}$$
   
   
   es una relación de equivalencia en el conjunto $\stackrel{n}{\wedge} E -\{ 0 \}$ y hay exactamente dos clases de equivalencia que seguiremos llamando los dos SENTIDOS DEL ESPACIO VECTORIAL REAL $E$.

   Para elementos equivalentes $\overline{u},\, \overline{v} \in \stackrel{n}{\wedge}E -\{ 0\}$ diremos para no violentar el lenguaje que ``SON DEL MISMO SENTIDO'' o ``TIENEN EL MISMO SENTIDO''.

   Un par $(E, {\frak F})$ donde ${\frak F}$ es uno de los dos sentidos de $E$ se dice ESPACIO VECTORIAL (REAL) ORIENTADO. Sobreentendiendo la elección de ${\frak F}$ (la ``ORIENTACIÓN'' de $E$) se habla por abuso del lenguaje (cómodo aunque ilógico) del ESPACIO VECTORIAL ORIENTADO $E$.

   El sentido ${\frak F}$ se dice el SENTIDO POSITIVO DEL ESPACIO VECTORIAL ORIENTADO $E$.

   Una base $(\vec{e}_1,\ldots,\vec{e}_n)$ de $E$ se dice BASE DE SENTIDO POSITIVO si $\vec{e}_1 \land \cdots \land \vec{e}_n \in {\frak F}$. En el caso contrario la base se dice de SENTIDO NEGATIVO.

Observación
Si $E$ es un espacio vectorial de dimensión finita $n$ sobre un cuerpo conmutativo ${\mathbb{K}}$, todo $n$-vector sobre $E$ es descomponible. En efecto al tomar una base arbitraria $(\vec{e}_1,\ldots,\vec{e}_n)$ de $E$, podemos escribir todo $n$-vector en la forma $\alpha (\vec{e}_1 \land \cdots \land \vec{e}_n) = \alpha \vec{e}_1 \land (\vec{e}_2 \land \cdots \land \vec{e}_n)$ con $\alpha \in {\mathbb{K}}$. Notamos también que un $n$-vector $\vec{x}_1 \land \cdots \land \vec{x}_n$ será no nulo si y sólo si $(\vec{x}_1,\ldots,\vec{x}_n)$ es una base de $E$.

Volviendo al caso de un espacio vectorial real $E$ de dimensión $n$, designemos por ${\cal B}$ al conjunto de todas las bases en $E$. En ${\cal B}$ introducimos una relación ``$\approx$'' por:

$$(\vec{x}_1,\ldots,\vec{x}_n) \approx (\vec{y}_1,\ldots,\vec{y... ...land \vec{x}_n \over \vec{y}_1 \land \cdots \land \vec{y}_n}> 0$$

(es decir, el determinante de la base $(\vec{x}_1,\ldots,\vec{x}_n)$ con respecto a la base $(\vec{y}_1,\ldots,\vec{y}_n)$ es positivo). Del teorema 1.4.17 se sigue inmediatamente que $\approx$ es una relación de equivalencia en ${\cal B}$ y que hay exactamente dos clases de equivalencia, a saber, la de una base fija $(\vec{u}_1,\vec{u}_2,\ldots,\vec{u}_n)$ y la de la base $(-\vec{u}_1,\vec{u}_2,\ldots,\vec{u}_n)$.

Las mismas conclusiones siguen más rápidamente al observar que

$$(\vec{x}_1,\ldots,\vec{x}_n)\, \approx \, (\vec{y}_1,\ldots,\vec{y}_n) \mbox{ en }{\cal B}$$

si y sólo si

$$\vec{x}_1 \land \cdots \land \vec{x}_n \sim \vec{y}_1 \land \cdots \land \vec{y}_n \mbox{ en }\stackrel{n}{\wedge} E - \{ 0 \}.$$

La aplicación:

$$\mbox{clase de} \; \; (\vec{x}_1,\ldots,\vec{x}_n) \mapsto \mbox{clase de}\;\; \vec{x}_1 \land \cdots \land \vec{x}_n$$

del conjunto cociente ${\cal B} / \approx$ en el conjunto cociente $\stackrel{n}{\wedge} E - \{ 0 \} / \sim$ está pues bien definida y es patentemente biyectiva.

Podemos pues, si deseamos, definir los dos sentidos de $E$ como las clases de equivalencia de bases de $E$ para la relación $\approx$.

Esta definición alternativa puede considerarse como más elemental que la primera pues, aunque presupone un conocimiento de determinantes, no exige aquél del álgebra exterior.

Siguiente: Menores de una matriz Arriba: Ampliación exterior de una Anterior: Determinante de un -uplo