




Siguiente: Orientación de un espacio
Arriba: Ampliación exterior de una
Anterior: Teoría de determinantes
Notemos que se verifica:
vale decir en definitiva:
 |
(28) |
Esta fórmula dice que
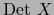 puede definirse también como la componente del
puede definirse también como la componente del  -vector
-vector
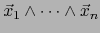 con respecto a la base de
con respecto a la base de
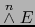 reducida al elemento
reducida al elemento
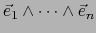 .
.
La fórmula (28) motiva también el convenio que haremos de designar el determinante del  -uplo
-uplo
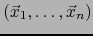 con respecto a la base
con respecto a la base
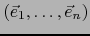 por la notación:
por la notación:
Observamos finalmente que, si ponemos:
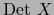 coincide con el determinante de la matriz
coincide con el determinante de la matriz 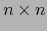 :
:
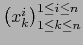 .
.
Teorema 4.16
Vale
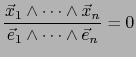 si y sólo si el
si y sólo si el  -uplo
-uplo
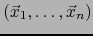 es linealmente dependiente.
es linealmente dependiente.
Demostración
La relación
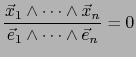 significa
significa
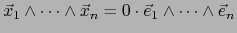 , o sea, simplemente:
, o sea, simplemente:
En virtud del teorema 1.3.4, la última relación se verifica si y sólo si el  -uplo
-uplo
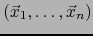 es linealmente dependiente.
es linealmente dependiente.

La notación (28) para el determinante de un  -uplo de vectores con respecto a una base resulta feliz debido al:
-uplo de vectores con respecto a una base resulta feliz debido al:
Demostración
- La relación
 significa
significa
relación que es cierta.
- Pongamos:
(29) y (30) significan respectivamente:
Llevando (31) a (32) conseguimos:
Pero esto es lo que afirma el inciso b. del enunciado.
- La afirmación c. se obtiene tomando en b.
y aplicando a.






Siguiente: Orientación de un espacio
Arriba: Ampliación exterior de una
Anterior: Teoría de determinantes
Guillermo M. Luna
2009-06-14
![]() -uplo
-uplo
![]() con respecto a la base
con respecto a la base
![]() por la notación:
por la notación:
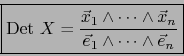
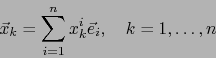
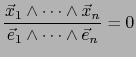 significa
significa
![]() , o sea, simplemente:
, o sea, simplemente:
![]() -uplo de vectores con respecto a una base resulta feliz debido al:
-uplo de vectores con respecto a una base resulta feliz debido al:


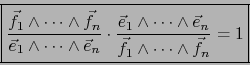
 significa
significa