Volvamos al caso general de espacios vectoriales sobre un cuerpo conmutativo arbitrario ![]() .
.
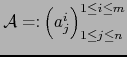 una matriz de tipo
una matriz de tipo 
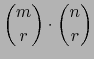 .
.
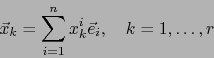
![\begin{displaymath}\fbox{${\displaystyle \vec{x}_1 \land \cdots \land \vec{x}_r ...
...m_{\vert H\vert = r } X_{[\![ 1, r]\!]}^H \, \overline{e}_H }$}\end{displaymath}](img1019.png)
Demostración
Tenemos:
![\begin{displaymath}\vec{x}_1 \land \cdots \land \vec{x}_r = \sum_{{\vert H\vert=...
...e}_H = \sum_{\vert H\vert=r} X^H_{[\![ 1,r ]\!]} \overline{e}_H\end{displaymath}](img1030.png)
Tres aplicaciones del teorema 1.4.18
Aplicación 1. Desarrollo del determinante de una matriz cuadrada con respecto a una columna y con respecto a una fila de ésta
Sea
![]() una matriz
una matriz ![]() de elementos en el cuerpo
de elementos en el cuerpo ![]() . Sean
. Sean
![]() los ``vectores columnas'' de la matriz
los ``vectores columnas'' de la matriz ![]() considerados
como elementos del espacio vectorial
considerados
como elementos del espacio vectorial
![]() . Tenemos:
. Tenemos:
De (35), (36) y (37) se sigue:
El escalar
![]() se llama el COFACTOR DEL ELEMENTO
se llama el COFACTOR DEL ELEMENTO ![]() de la matriz
de la matriz ![]() .
.
Por el teorema 1.4.15
![]() no cambia si las columnas de
no cambia si las columnas de ![]() se cambian por filas, o sea,
se cambian por filas, o sea, ![]() cambia por
cambia por ![]() . Vale, pues, también la fórmula:
. Vale, pues, también la fórmula:
Aplicación 2. Fórmula para la inversa de una matriz cuadrada inversible
Mantengamos las notaciones de la aplicación 1.
![]() pongamos
pongamos
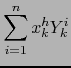 es un desarrollo del determinante de la matriz obtenida al sustituir la fila número
es un desarrollo del determinante de la matriz obtenida al sustituir la fila número ![\begin{displaymath}\sum_{i=1}^n x_i^h Y_k^i = \delta_k^h\, \mbox{\rm Det } {\cal X} \quad \forall \, h,\, k \in [\![ 1,n ]\!]\end{displaymath}](img1056.png)
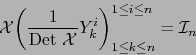
La fórmula (46) no se presta fácilmente a evaluación por calculadoras. Su importancia estriba en que revela la estructura de la matriz inversa. Quizás la más importante información que suministra es que los elementos de ![]() se expresan
como fracciones racionales en los elementos de
se expresan
como fracciones racionales en los elementos de ![]() .
.
Aplicación 3 (Generalización de la aplicación 1).
Sea
![]() una matriz de tipo
una matriz de tipo ![]() de elementos en el cuerpo conmutativo
de elementos en el cuerpo conmutativo
![]() . Sean
. Sean
![]() y
y
![]() una parte
de
una parte
de ![]() , arbitrariamente fijada, de cardinalidad
, arbitrariamente fijada, de cardinalidad ![]() .
Designamos por
.
Designamos por ![]() el complemento de
el complemento de ![]() en
en ![]() (luego
(luego
![]() ).
).
Vale la fórmula:

Demostración
Sean
 ,
,
![]() los vectores columnas de
los vectores columnas de ![]() .
.
Si
![]() con
con
![]() , designamos por
, designamos por
![]() el
el ![]() -vector
-vector
![]() . Análogamente definimos el
. Análogamente definimos el ![]() -vector
-vector
![]() .
.
Tenemos:
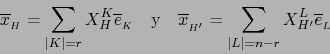
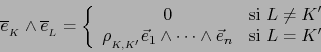
Escribimos ![]() si la primera de las diferencias
si la primera de las diferencias
![]() (
(
![]() ) que no es cero, es positiva.
) que no es cero, es positiva.
Se comprueba que la relación ``![]() '' es una relación de orden total, estricta, en el conjunto de todas las partes de
'' es una relación de orden total, estricta, en el conjunto de todas las partes de ![]() de cardinalidad
de cardinalidad ![]() . Se llama la RELACIÓN DE ORDEN LEXICOGRÁFICA.
. Se llama la RELACIÓN DE ORDEN LEXICOGRÁFICA.
 . Aquí
. Aquí
Demostración
Sea ![]() una parte de
una parte de ![]() tal que
tal que ![]() . Pongamos
. Pongamos
![]() con
con
![]() . Tenemos:
. Tenemos:
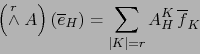
Combinando el teorema 1.4.19 con el teorema 1.4.8 obtenemos inmediatamente:
Consecuencia. (Rango de una matriz en función de sus menores)
El rango ![]() de una matriz
de una matriz ![]() , si no es nulo, es igual al mayor entero natural
, si no es nulo, es igual al mayor entero natural ![]() tal que existe por lo menos un menor de orden
tal que existe por lo menos un menor de orden ![]() de
de ![]() que no sea nulo. Más precisamente:
que no sea nulo. Más precisamente:
Si ![]() , existe un menor no nulo de orden
, existe un menor no nulo de orden ![]() de la matriz
de la matriz ![]() .
.
Si ![]() , todos los menores de orden
, todos los menores de orden ![]() de
de ![]() son nulos.
son nulos.
Este enunciado es clásico. Sin embargo, su prueba sin el uso del álgebra exterior es engorrosa. Multivectores descomponibles