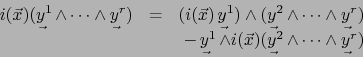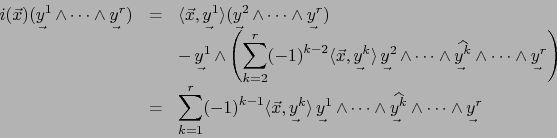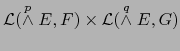 en
en
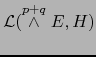 llamada MULTIPLICACIÓN EXTERIOR CON RESPECTO A LA APLICACIÓN BILINEAL
llamada MULTIPLICACIÓN EXTERIOR CON RESPECTO A LA APLICACIÓN BILINEAL 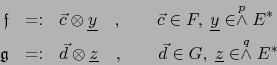
valga:
Para
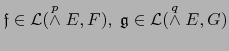 arbitrarios se tiene, con las notaciones del teorema 2.3.2,
arbitrarios se tiene, con las notaciones del teorema 2.3.2,
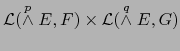 en
en
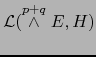 llamada MULTIPLICACIÓN EXTERIOR CON RESPECTO A LA APLICACIÓN BILINEAL
llamada MULTIPLICACIÓN EXTERIOR CON RESPECTO A LA APLICACIÓN BILINEAL 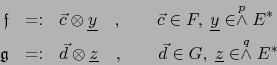
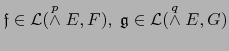 arbitrarios se tiene, con las notaciones del teorema 2.3.2,
arbitrarios se tiene, con las notaciones del teorema 2.3.2,
Demostración
Unicidad de la aplicación ![]() . Supongamos que la aplicación deseada
. Supongamos que la aplicación deseada ![]() existe. Por hipótesis, el elemento
existe. Por hipótesis, el elemento
![]() de
de
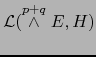 está dado sin ambigüedad por la fórmula (8) en el caso particular de ser
está dado sin ambigüedad por la fórmula (8) en el caso particular de ser
![]() elementos simples de sendos espacios
elementos simples de sendos espacios
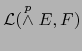 ,
,
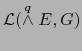 . En el caso general de
. En el caso general de
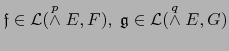 , podemos, en virtud del teorema 2.4.2, representar
, podemos, en virtud del teorema 2.4.2, representar ![]() y
y ![]() como:
como:
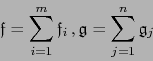
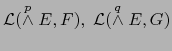 . Por bilinealidad tenemos:
. Por bilinealidad tenemos:
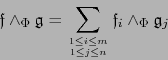
Existencia de la aplicación ![]() . Sean
. Sean
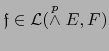 ,
,
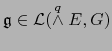 .
Definimos una aplicación:
.
Definimos una aplicación:
![]() por la fórmula:
por la fórmula:
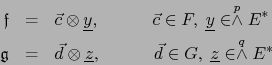
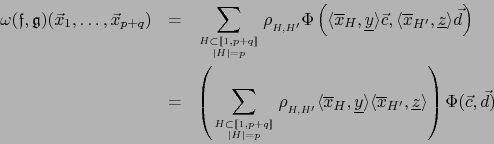
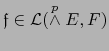 ,
,
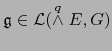 arbitrarios, podemos escribir en virtud del
teorema 2.4.2:
arbitrarios, podemos escribir en virtud del
teorema 2.4.2:

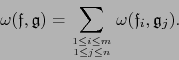
Por la propiedad universal de la terna
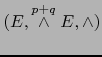 existe una aplicación lineal única
existe una aplicación lineal única
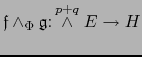 que hace conmutativo el diagrama:
que hace conmutativo el diagrama:
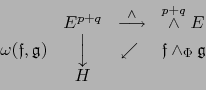
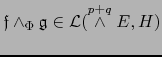 se expresa explícitamente por la fórmula (8) del enunciado.
se expresa explícitamente por la fórmula (8) del enunciado.
Finalmente, la fórmula (11) reza ahora:
![]() en caso de ser
en caso de ser
![]() y
y
![]() .
.
Con ello, la prueba de la existencia de la multiplicación exterior de ![]() está completa.
está completa.
![]()
Casos particulares
Los casos particulares más simples son:
Ambos casos pueden darse simultáneamente, es decir, cuando se tenga
![]() y
y ![]() sea la multiplicación usual en
sea la multiplicación usual en ![]() . En este caso, el teorema 2.4.2 se reduce a 2.3.2.
. En este caso, el teorema 2.4.2 se reduce a 2.3.2.
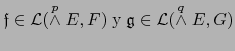 . Al escribir:
. Al escribir:

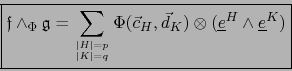
Producto interno de un vector por una forma exterior
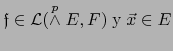 . La aplicación
. La aplicación
 , o sea, una forma exterior sobre
, o sea, una forma exterior sobre
Demostración
 vale:
vale:
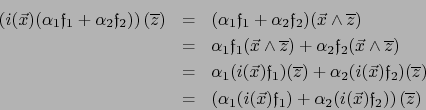
Casos particulares.
A. Puesto que
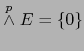 si
si ![]() entonces
entonces ![]() vale cero sobre el espacio
vale cero sobre el espacio
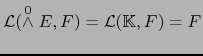
B. Sea ![]() una forma exterior de grado 1:
una forma exterior de grado 1:
![]() . Al considerar
. Al considerar
![]() como elemento de
como elemento de
![]() tenemos
tenemos
![]() :
:
![]() , o sea, al identificar según el teorema 2.4.1, la aplicación
, o sea, al identificar según el teorema 2.4.1, la aplicación
![]() con el elemento
con el elemento
![]() de
de ![]() :
:
C. En el caso particular
![]() ,
,
![]() es una aplicación lineal de
es una aplicación lineal de
![]() en
en
![]() . La fórmula de definición reza:
. La fórmula de definición reza:
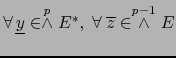
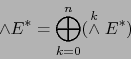
Más generalmente, ![]() designará el operador
designará el operador ![]() aplicado al espacio vectorial
aplicado al espacio vectorial
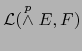 (debemos resignarnos a
omitir en la notación una referencia explícita al espacio
(debemos resignarnos a
omitir en la notación una referencia explícita al espacio ![]() ).
).
Demostración
Consideremos todos los ![]() como operandos sobre
como operandos sobre
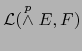 . Obtenemos
. Obtenemos
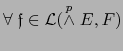 y
y
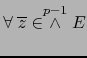 :
:

Demostración
Tenemos
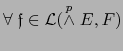 y
y
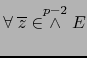 :
:
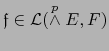 ,
,
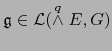 vale:
vale:
Demostración
Basta probar que los dos miembros de la fórmula por demostrar coinciden sobre todo
![]() -vector descomponible
-vector descomponible
![]() sobre
sobre ![]() .
Ahora bien:
.
Ahora bien:

Demostración
Haremos la demostración por inducción sobre el número ![]() de factores. Para
de factores. Para ![]() la fórmula se reduce a:
la fórmula se reduce a:
Supongamos ahora ![]() y la fórmula ya probada para
y la fórmula ya probada para ![]() . Escribiendo
. Escribiendo
![]() como producto exterior de una forma de grado 1 por una forma de grado
como producto exterior de una forma de grado 1 por una forma de grado ![]() y aplicando la fórmula del teorema 2.4.8, obtenemos:
y aplicando la fórmula del teorema 2.4.8, obtenemos: