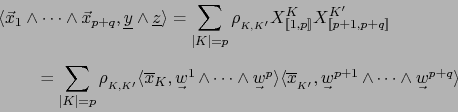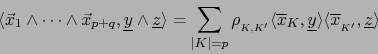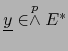 y
y
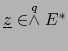 tenemos
tenemos
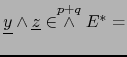 [dual de
[dual de
Si
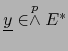 y
y
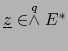 tenemos
tenemos
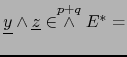 [dual de
[dual de
![]() ]. Es deseable caracterizar la forma exterior
]. Es deseable caracterizar la forma exterior
![]() de grado
de grado ![]() , obteniendo sus valores sobre los elementos de
, obteniendo sus valores sobre los elementos de
![]() o, por lo menos, sobre los
o, por lo menos, sobre los ![]() -vectores descomponibles. Esta tarea la cumple:
-vectores descomponibles. Esta tarea la cumple:
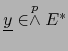 y
y
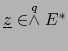 . Para todo
. Para todo 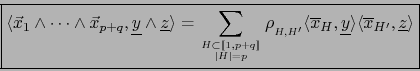
Las notaciones de esta fórmula son las siguientes:
Si
![]() y
y ![]() , explícitamente
, explícitamente
![]() , donde los dígitos están ordenados
, donde los dígitos están ordenados
![]() ,
,
![]() designa el
designa el ![]() -vector descomponible
-vector descomponible
![]() .
. ![]() , parte de
, parte de
![]() de cardinalidad
de cardinalidad ![]() , es, por definición, el complemento de
, es, por definición, el complemento de ![]() con respecto a
con respecto a
![]() . Si
. Si
![]() , con
, con
![]() , análogamente a la definición de
, análogamente a la definición de
![]() ,
,
![]() se define como el
se define como el ![]() -vector descomponible
-vector descomponible
![]() .
.
Demostración
Basta probar el teorema suponiendo que no sólo el ![]() -vector
considerado, sino también las formas exteriores
-vector
considerado, sino también las formas exteriores
![]() son descomponibles.
Ponemos pues:
son descomponibles.
Ponemos pues:
Al designar por
![]() y
y
![]() menores de sendos órdenes
menores de sendos órdenes ![]() ,
, ![]() del determinante a la derecha de (12), obtenemos:
del determinante a la derecha de (12), obtenemos: