#MATH2676# DE A LA NUEVA BASE
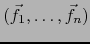 . Puesto que
. Puesto que
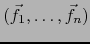 es una familia linealmente independiente en
es una familia linealmente independiente en  , la matriz
, la matriz 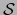 es una matriz inversible. Introducimos también las bases
es una matriz inversible. Introducimos también las bases
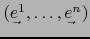 de
de 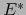 duales de sendas bases
duales de sendas bases
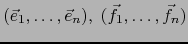 de
de  .
Sea
.
Sea 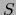 el único endomorfismo lineal de
el único endomorfismo lineal de  tal que:
tal que:
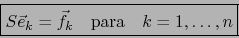 |
(2) |
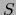 es de hecho un automorfismo lineal de
es de hecho un automorfismo lineal de  . Ya que por (1) y (2):
. Ya que por (1) y (2):
la matriz de transición 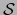 es la matriz del automorfismo
es la matriz del automorfismo 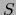 con respecto a la antigua base
con respecto a la antigua base
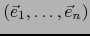 de E.
de E.
Aplicando el operador 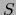 a ambos miembros de (1), obtenemos:
a ambos miembros de (1), obtenemos:
o sea, teniendo en cuenta (2):
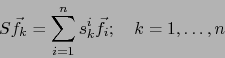 |
(3) |
Estas fórmulas muestran que la matriz de transición 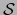 es también la matriz del automorfismo
es también la matriz del automorfismo 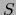 con respecto a la nueva base
con respecto a la nueva base
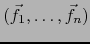 de
de  .
.
Pasemos al automorfismo dual 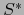 de
de 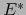 .
Por el teorema 2.2.6 las fórmulas (3) equivalen a:
.
Por el teorema 2.2.6 las fórmulas (3) equivalen a:
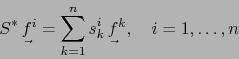 |
(4) |
Por otra parte,
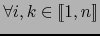 en virtud de (2)
en virtud de (2)
de donde:
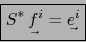 |
(5) |
Comparando con (4), obtenemos la fórmula ``dual'' de (1):
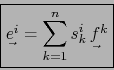 |
(6) |
Al pasar de (1) y (6) notamos un ``doble fenómeno de inversión'', a saber:
- Las fórmulas (1) expresan los elementos de la nueva base de
 en función de la antigua base. Pero las fórmulas (6) expresan los elementos de la antigua base dual de
en función de la antigua base. Pero las fórmulas (6) expresan los elementos de la antigua base dual de 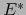 en función de la nueva.
en función de la nueva.
- En cada fórmula (1) se fija el índice inferior
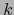 (índice de columna) de
(índice de columna) de 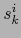 . Pero en cada fórmula (6) es fijo el índice superior
. Pero en cada fórmula (6) es fijo el índice superior 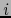 (índice de fila) de
(índice de fila) de 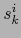 ; o, si se quiere:
; o, si se quiere:
La fórmula número 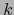 en (1) pone en obra la columna número
en (1) pone en obra la columna número 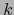 de
de 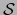 .
.
La fórmula número 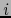 en (6) pone en obra la fila número
en (6) pone en obra la fila número 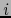 de
de 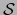 .
.





Siguiente: Cambio de base en
Arriba: Cambio de base
Anterior: Cambio de base
Guillermo M. Luna
2009-06-14
![]() un espacio vectorial de dimensión finita
un espacio vectorial de dimensión finita ![]() . Consideremos en
. Consideremos en ![]() una ``antigua base''
una ``antigua base''
![]() y una ``nueva base''
y una ``nueva base''
![]() .
Rigen unas relaciones:
.
Rigen unas relaciones:
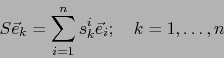
![]() a ambos miembros de (1), obtenemos:
a ambos miembros de (1), obtenemos:
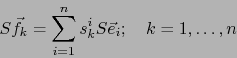
![]() de
de ![]() .
Por el teorema 2.2.6 las fórmulas (3) equivalen a:
.
Por el teorema 2.2.6 las fórmulas (3) equivalen a:
![]() en (1) pone en obra la columna número
en (1) pone en obra la columna número ![]() de
de ![]() .
.
![]() en (6) pone en obra la fila número
en (6) pone en obra la fila número ![]() de
de ![]() .
.