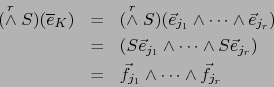Siguiente: Cambio de componentes
Arriba: Cambio de base
Anterior: Cambio de base en
Sea
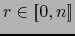 . Sea
. Sea
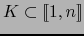 tal que
tal que 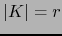 . Escribimos
. Escribimos
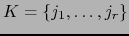 ,
,
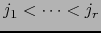 . Vale en virtud de (2):
. Vale en virtud de (2):
O sea:
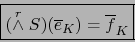 |
(7) |
Por otra parte, por el teorema 1.4.19, la matriz del automorfismo
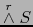 del espacio vectorial
del espacio vectorial
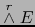 con respecto a cualquiera de las bases
con respecto a cualquiera de las bases
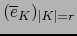 ,
,
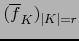 de este espacio es
de este espacio es
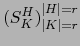 , la matriz de los menores de orden
, la matriz de los menores de orden 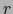 de la matriz
de la matriz 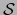 . Tenemos pues:
. Tenemos pues:
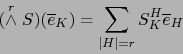 |
(8) |
y
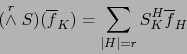 |
(9) |
Al comparar (7) con (8) obtenemos:
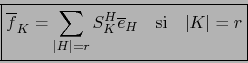 |
(10) |
fórmula que generaliza (1).
También por los teoremas 2.2.6 y 2.3.3 la fórmula (9) equivale a:
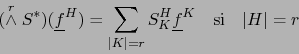 |
(11) |
Por otra parte, usando (7):
y esto dice que:
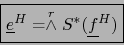 |
(12) |
fórmula que generaliza (5).
Finalmente, comparando (11) con (12) llegamos a:
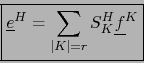 |
(13) |
fórmula que generaliza (7).
Como en la subsección 2.5.1, cabe señalar un ``doble fenómeno de inversión'' al pasar de las fórmulas (10) a las fórmulas (13).





Siguiente: Cambio de componentes
Arriba: Cambio de base
Anterior: Cambio de base en
Guillermo M. Luna
2009-06-14
![]() . Sea
. Sea
![]() tal que
tal que ![]() . Escribimos
. Escribimos
![]() ,
,
![]() . Vale en virtud de (2):
. Vale en virtud de (2):