




Siguiente: Cálculo en variedades diferenciales
Arriba: El operador de Hodge
Anterior: Caracterización geométrica del producto
Dirección.
Equivalentemente:
Magnitud. Por la fórmula de Cauchy-Binet:
o sea:
donde el segundo miembro es el volumen ``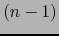 -dimensional'' en el espacio vectorial euclidiano
-dimensional'' en el espacio vectorial euclidiano
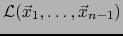 de dimensión
de dimensión 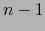 .
.
Sentido. El 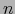 -uplo
-uplo
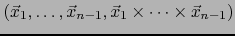 es de sentido positivo, pues:
es de sentido positivo, pues:
Hasta aquí nuestra introducción algebraica.
Guillermo M. Luna
2009-06-14
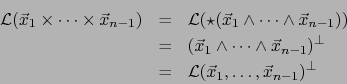
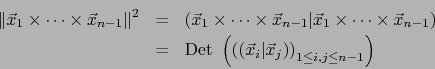
![]() -uplo
-uplo
![]() es de sentido positivo, pues:
es de sentido positivo, pues: