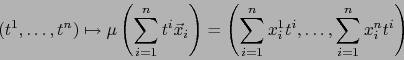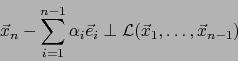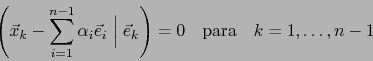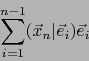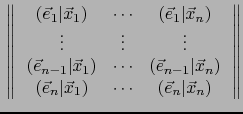Siguiente: Caracterización geométrica del producto
Arriba: El operador de Hodge
Anterior: El operador de Hodge
Patentemente si también 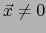 :
:
Sea
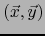 un par linealmente independiente de vectores de un espacio vectorial euclidiano orientado de
dimensión tres.
El PRODUCTO VECTORIAL
un par linealmente independiente de vectores de un espacio vectorial euclidiano orientado de
dimensión tres.
El PRODUCTO VECTORIAL
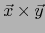 se caracteriza geométricamente como sigue:
se caracteriza geométricamente como sigue:
- Dirección:
-
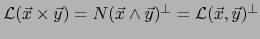 , vale decir:
, vale decir:
- Magnitud:
- Por el teorema 3.3.15:
o sea:
- Sentido.
- La terna
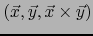 es una
base de sentido positivo de E.
es una
base de sentido positivo de E.
En efecto
Ejemplo:  arbitrario,
arbitrario, 
Este ejemplo es una generalización de los precedentes. Consideramos el operador
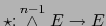 . Por
el teorema 3.3.10, todo
. Por
el teorema 3.3.10, todo 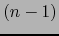 -vector, elemento de
-vector, elemento de
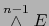 es descomponible. Para todo
es descomponible. Para todo 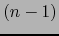 -uplo
-uplo
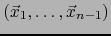 de
vectores de
de
vectores de  definimos:
definimos:
El vector
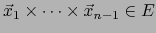 se dice ser el PRODUCTO VECTORIAL del
se dice ser el PRODUCTO VECTORIAL del 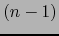 -uplo
-uplo
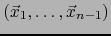 de vectores de
de vectores de  .
.
La aplicación
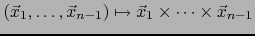 es una
aplicación, de
es una
aplicación, de 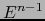 en
en  ,
, 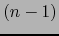 -lineal alternada.
-lineal alternada.
Vale
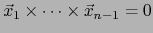 si y sólo si el
si y sólo si el 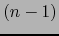 -uplo
-uplo
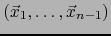 es linealmente dependiente.
es linealmente dependiente.
Por definición del operador 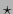 , el vector
, el vector
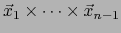 es el único de
es el único de  que cumple:
que cumple:
![\begin{displaymath}\mbox{\fbox{${\displaystyle \left( \vec{x}_1 \times \cdots\ti...
...dots, \vec{x}_{n-1}, \vec y] \quad \forall \, \vec y \in E}$}}
\end{displaymath}](img2645.png) |
(56) |
Observamos que si
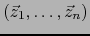 es un
es un  -uplo de vectores de
-uplo de vectores de  , debido a la ley de
conmutación en álgebra exterior se tiene
, debido a la ley de
conmutación en álgebra exterior se tiene
![$\forall \, k \in [\![ 1,n ]\!]$](img301.png) :
:
Junto con (56), esta regla entraña la, así llamada, LEY DEL PRODUCTO MIXTO:
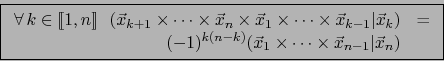 |
(57) |
Observamos que si
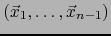 es un
es un 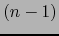 -uplo linealmente independiente de vectores de
-uplo linealmente independiente de vectores de  , tenemos:
, tenemos:
En otras palabras:
![\begin{displaymath}\mbox{\fbox{${\displaystyle \vec{x}_1 \times \cdots \times \v...
...1} \,\bot\, \vec{x}_k \quad \forall k \in [\![ 1,n-1 ]\!] }$}}
\end{displaymath}](img2650.png) |
(58) |
Fórmulas.
A) Sean
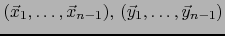 dos
dos 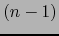 -uplos de vectores de
-uplos de vectores de  . Por
definición del producto vectorial y el teorema 3.3.15 tenemos:
. Por
definición del producto vectorial y el teorema 3.3.15 tenemos:
o sea mediante el teorema 3.2.1:
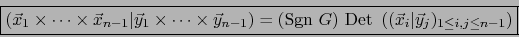 |
(59) |
Esta es la FÓRMULA DE CAUCHY-BINET PARA PRODUCTOS VECTORIALES EN DIMENSIÓN  .
.
B) Consideremos un 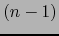 -uplo
-uplo
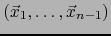 y un
y un 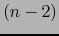 -uplo
-uplo
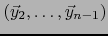 de vectores de
de vectores de  . Por la fórmula (58) del producto vectorial, el vector:
. Por la fórmula (58) del producto vectorial, el vector:
si no es nulo es ortogonal al vector
 , luego será una combinación lineal de
, luego será una combinación lineal de
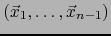 . Busquemos los coeficientes de tal combinación lineal.
. Busquemos los coeficientes de tal combinación lineal.
Sin ninguna hipótesis sobre los vectores concernidos, tenemos:
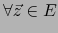 :
:
De ahí, por la fórmula (59) (de Cauchy-Binet):
Desarrollando el determinante a la derecha de esta fórmula con respecto a la primera columna, conseguimos:
Finalmente, por ser 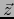 arbitrario
arbitrario
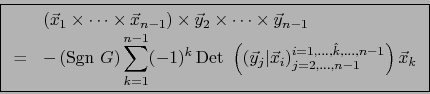 |
(60) |
Esta es la FÓRMULA DEL PRODUCTO VECTORIAL REITERADO, que generaliza la fórmula del doble producto vectorial
del ejemplo precedente.
Observación
En el caso 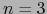 dedujimos de la fórmula del doble producto vectorial, una relación lineal no trivial entre cuatro
vectores de
dedujimos de la fórmula del doble producto vectorial, una relación lineal no trivial entre cuatro
vectores de  que constituyen una familia de rango 3. Generalizando: ¿cómo obtener una relación lineal
no trivial entre
que constituyen una familia de rango 3. Generalizando: ¿cómo obtener una relación lineal
no trivial entre 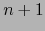 vectores
vectores
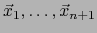 de nuestro espacio vectorial
de nuestro espacio vectorial  de dimensión
de dimensión  , que constituya
una familia de rango
, que constituya
una familia de rango  ?
?
Aunque no veo cómo la fórmula (60) pueda servir para ello (y dudo que pueda), vamos a resolver el problema por un método distinto (y más natural).
Sea
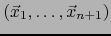 una familia de
una familia de 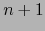 vectores de nuestro espacio
vectores de nuestro espacio  de dimensión
de dimensión  . Sea
. Sea 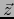 un vector arbitrario de
un vector arbitrario de  y sea
y sea
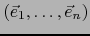 una base de sentido positivo de
una base de sentido positivo de  . Afirmamos que:
. Afirmamos que:
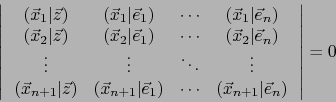 |
(61) |
En efecto, uno de los vectores
 es una combinación lineal de los restantes. Si lo es, por ejemplo,
es una combinación lineal de los restantes. Si lo es, por ejemplo,  , el último
renglón de la matriz a la izquierda de (61) será la correspondiente combinación lineal de los demás renglones. Luego la relación (61) es cierta.
Al desarrollar el determinante (61) con respecto a la primera columna obtenemos:
, el último
renglón de la matriz a la izquierda de (61) será la correspondiente combinación lineal de los demás renglones. Luego la relación (61) es cierta.
Al desarrollar el determinante (61) con respecto a la primera columna obtenemos:
 |
(62) |
Pero, por la observación después del corolario del teorema 3.3.15 (o sea, después de la identidad de
Cauchy-Binet para productos volúmicos), vale:
Llevando a (62), conseguimos:
De ahí , por la arbitrariedad de 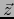 :
:
![\begin{displaymath}\mbox{\fbox{${\displaystyle {\displaystyle \sum_{k=1}^{n+1} (...
...s,\widehat{\vec{x}_k},\ldots,\vec{x}_{n+1}] \vec{x}_k =0 }}$}}
\end{displaymath}](img2671.png) |
(63) |
(63) es una relación lineal entre los vectores
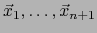 . Si éstos
constituyen una familia de rango
. Si éstos
constituyen una familia de rango  , dicha relación lineal es no trivial.
, dicha relación lineal es no trivial.
Fórmulas analíticas
Sea
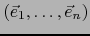 una base de sentido positivo de
una base de sentido positivo de  y sea
y sea
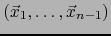 una familia
arbitraria de vectores de
una familia
arbitraria de vectores de  . Escribimos cada vector
. Escribimos cada vector
 , con
, con
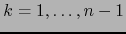 , e introducimos la
matriz
, e introducimos la
matriz
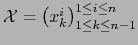 de tipo
de tipo
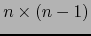 .
.
![$\forall \, i \in [\![ 1 , n ]\!]$](img2676.png) designamos por
designamos por 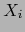 el menor de orden
el menor de orden 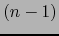 de la matriz
de la matriz 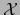 , determinante de la
matriz
, determinante de la
matriz
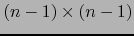 obtenida al privar la matriz
obtenida al privar la matriz 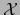 de su fila número
de su fila número 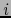 , o sea, según nuestras notaciones usuales:
, o sea, según nuestras notaciones usuales:
Aplicando el teorema 1.4.18 (``componentes de un multivector descomponible''), obtenemos:
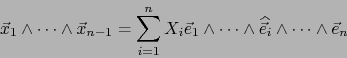 |
(64) |
Usamos ahora la fórmula del comentario después de lema 3.3.2 que reza:
y suministra en particular:
 |
(65) |
de donde, por (64):
La componente covariante de índice  de
de
es pues:
En el caso particular de ser  un espacio vectorial euclidiano y
un espacio vectorial euclidiano y
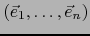 una
base O.N.P. de
una
base O.N.P. de  , las componentes a la vez covariantes y contravariantes del producto vectorial
, las componentes a la vez covariantes y contravariantes del producto vectorial
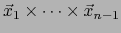 son
simplemente:
son
simplemente:
Se tiene, pues, en este caso:
Finalmente, en el caso considerado, la fórmula (65) entraña:
Digresión: Volumen de un paralelotopo
A) Sea  un espacio vectorial euclidiano de dimensión
un espacio vectorial euclidiano de dimensión  . Orientamos
. Orientamos  de modo arbitrario e introducimos una
base calibrada arbitraria
de modo arbitrario e introducimos una
base calibrada arbitraria
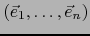 de
de  . Sea
. Sea  la biyección de
la biyección de  sobre
sobre
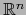 dada por:
dada por:
Si
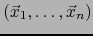 es un
es un  -uplo linealmente independiente de
-uplo linealmente independiente de  , el conjunto:
, el conjunto:
se llama PARALELOTOPO DE ARISTAS
 .
Pongamos
.
Pongamos
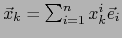 ,
, 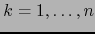 . La aplicación:
. La aplicación:
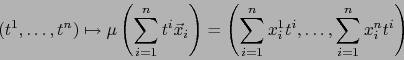 |
(66) |
es un automorfismo lineal de
 de determinante
de determinante
luego automorfismo  de
de
 de jacobiano constante
de jacobiano constante
![$[\vec{x}_1,\ldots,\vec{x}_n]$](img2320.png) . El conjunto
cerrado, luego medible,
. El conjunto
cerrado, luego medible,
 es la imagen
por el automorfismo (66) del cubo:
es la imagen
por el automorfismo (66) del cubo:
se sigue, pues, de la fórmula de cambio de variables en integrales de Lebesgue, que la medida de Lebesgue o, como diremos, el VOLUMEN del conjunto
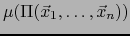 , es:
, es:
![\begin{displaymath}
\mbox{\rm vol }\,\mu \, \left( \Pi (\vec{x}_1,\ldots,\vec{x}...
...vol }Q = \left\vert [\vec{x}_1,\ldots,\vec{x}_n ] \right\vert
\end{displaymath}](img2697.png) |
(67) |
El segundo miembro de (67) es independiente de la base calibrada elegida
 y también de la orientación de
y también de la orientación de  . Se llama simplemente el VOLUMEN DEL PARALELOTOPO
. Se llama simplemente el VOLUMEN DEL PARALELOTOPO
 y se designa por
y se designa por
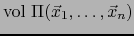 . Destacamos:
. Destacamos:
![\begin{displaymath}\mbox{\fbox{${\displaystyle \mbox{\rm vol }\Pi (\vec{x}_1,\ld...
..._n) = \left\vert [\vec{x}_1,\ldots,\vec{x}_n ] \right\vert}$}}
\end{displaymath}](img2699.png) |
(68) |
La fórmula (68) justifica la denominación ``producto volúmico'' para el valor
![$[\vec{x}_1,\ldots,\vec{x}_n]$](img2320.png) .
Transformando el segundo miembro de (68) por la identidad de Lagrange, obtenemos:
.
Transformando el segundo miembro de (68) por la identidad de Lagrange, obtenemos:
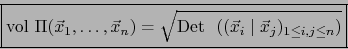 |
(69) |
El segundo miembro de (69) es la raíz cuadrada del gramiano del  -uplo
-uplo
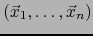 .
.
La fórmula (69) presenta la ventaja de ya no hacer referencia a ninguna orientación de  . Se aplica cómodamente a paralelotopos (``de dimensión inferior'') en
subespacios de
. Se aplica cómodamente a paralelotopos (``de dimensión inferior'') en
subespacios de  .
.
B) Este inciso no se usará más adelante, pero pensamos que debería interesar a futuros profesores de matemática.
Consideramos de nuevo el paralelotopo
 . Introducimos una base O.N.
. Introducimos una base O.N.
 del subespacio
del subespacio
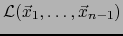 de
de  y la completamos a una base O.N.
y la completamos a una base O.N.
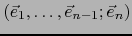 de
de  .
.
Afirmamos que existe un único punto
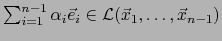 llamado
PROYECCIÓN ORTOGONAL de
llamado
PROYECCIÓN ORTOGONAL de 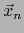 sobre el subespacio
sobre el subespacio
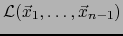 , tal que:
, tal que:
La condición para ello reza:
y suministra
![$\alpha_k = (\vec{x}_n \vert \vec{e}_k) \; \forall k \in [\![ 1, n-1 ]\!]$](img2708.png) , probando nuestra afirmación.
, probando nuestra afirmación.
La proyección ortogonal de 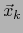 sobre el subespacio
sobre el subespacio
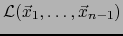 es, pues, el punto:
es, pues, el punto:
La distancia euclidiana 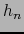 de
de 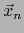 a esta proyección ortogonal se llama la ALTURA DEL PARALELOTOPO #MATH3728# RELATIVA
a la base
a esta proyección ortogonal se llama la ALTURA DEL PARALELOTOPO #MATH3728# RELATIVA
a la base
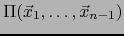 de dicho paralelotopo. Aquí
de dicho paralelotopo. Aquí
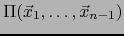 es un
paralelotopo (``de dimensión
es un
paralelotopo (``de dimensión 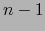 '') en el espacio vectorial euclidiano
'') en el espacio vectorial euclidiano
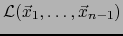 . Tenemos:
. Tenemos:
o sea:
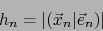 |
(70) |
Finalmente, aseveramos que vale la fórmula:
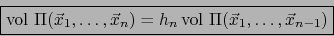 |
(71) |
donde
 es el volumen (``
es el volumen (``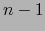 -dimensional'') de la base
-dimensional'') de la base
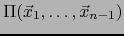 .
.
En efecto, tenemos:
Pero
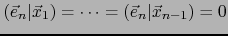 , pues
, pues
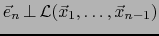 , luego,
al desarrollar el determinante en (72) con respecto a la
, luego,
al desarrollar el determinante en (72) con respecto a la  -ésima fila, conseguimos:
-ésima fila, conseguimos:
que, teniendo en cuenta a (72), se ve que es equivalente a (71).
Fórmulas análogas a (71) se obtiene también para los índices 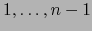 en vez de
en vez de  .
.





Siguiente: Caracterización geométrica del producto
Arriba: El operador de Hodge
Anterior: El operador de Hodge
Guillermo M. Luna
2009-06-14
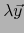 con
con
 , tal que se cumple
, tal que se cumple
 .
.
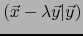 suministra únicamente
suministra únicamente
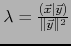 , de donde
dicho vector es
, de donde
dicho vector es
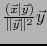 .
Se llama la PROYECCIÓN ORTOGONAL DEL VECTOR SOBRE EL VECTOR .
.
Se llama la PROYECCIÓN ORTOGONAL DEL VECTOR SOBRE EL VECTOR .
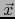 a dicha proyección ortogonal, a saber, el valor
a dicha proyección ortogonal, a saber, el valor
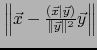 , se calcula por:
, se calcula por:
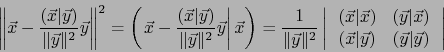
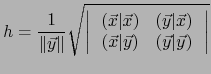 es la ``altura'' del ``paralelogramo
es la ``altura'' del ``paralelogramo
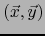 '' relativa a la ``base
'' relativa a la ``base 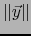 '' de
dicho paralelogramo.
'' de
dicho paralelogramo.
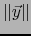 por la correspondiente altura
por la correspondiente altura 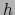 es por definición el ´AREA DEL PARALELOGRAMO
es por definición el ´AREA DEL PARALELOGRAMO
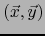 :
:
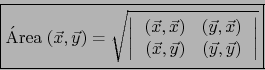
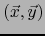 ).
).
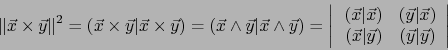
![\begin{eqnarray*}[\vec{z}_1,\ldots,\vec{z}_n]&=& [\vec{z}_1\wedge \cdots \wedge\...
...)} [\vec{z}_{k+1},\ldots,\vec{z}_n, \vec{z}_1,\ldots,\vec{z}_k]
\end{eqnarray*}](img2647.png)
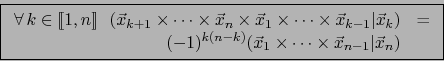
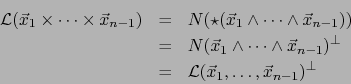

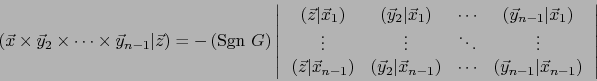
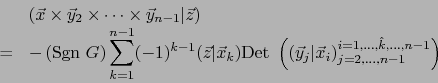
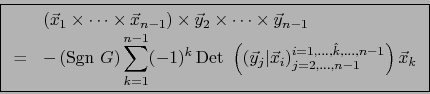
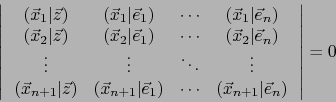

![\begin{displaymath}\sum_{k=1}^{n+1} (-1)^{k-1} [\vec{x}_1,\ldots,\widehat{\vec{x}_k},\ldots,\vec{x}_{n+1}] (\vec{x}_k \vert \vec{z}) =0\end{displaymath}](img2670.png)
![\begin{displaymath}\mbox{\fbox{${\displaystyle {\displaystyle \sum_{k=1}^{n+1} (...
...s,\widehat{\vec{x}_k},\ldots,\vec{x}_{n+1}] \vec{x}_k =0 }}$}}
\end{displaymath}](img2671.png)
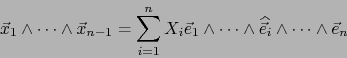
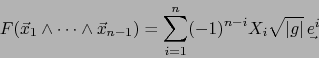
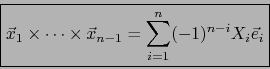
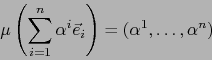
![\begin{displaymath}\fbox{${\displaystyle {\displaystyle \Pi (\vec{x}_1,\ldots,\v...
...\le t^i \le 1 \; \forall \, i \in [\![ 1, n ]\!] \right\} } }$}\end{displaymath}](img2690.png)