Siguiente: Aplicaciones afines Arriba: Espacios afines Anterior: Espacios afines

Primeras consecuencias de los axiomas

A) Vale

$$\fbox{${\displaystyle i^\prime)\ \ \overrightarrow {AA}=0 \quad \forall \, A \in {\cal E} }$}$$

(Es decir, es cierto también el recíproco del axioma i).) Esto se ve inmediatamente al tomar $B=C=A$ en la relación de Chasles.

B) Vale:

$$\fbox{${\displaystyle ii^\prime)\ \ \overrightarrow {BA}=-\overrightarrow {AB} \quad \forall \, A,B \in \cal E}$}$$

En efecto, al tomar $C=A$ en la relación de Chasles obtenemos:

$$\overrightarrow {AB}+ \overrightarrow {BA} = \overrightarrow {AA}$$

o sea por $i^\prime$):

$$\overrightarrow {AB} + \overrightarrow {BA}=0$$

C) El punto Q del axioma iii) es único.

En efecto, supongamos que se tiene simultáneamente: $\overrightarrow {PQ}= \vec{u}$ y $\overrightarrow {PQ^\prime}= \vec u$. De ahí se sigue:

$$- \overrightarrow {PQ^\prime}+ \overrightarrow {PQ}=0$$

o sea, usando $ii^\prime$):

$$\overrightarrow {Q^\prime P} + \overrightarrow {PQ}=0$$

o sea, por la relación de Chasles: $\overrightarrow {Q^\prime Q}=0$. Finalmente, por el axioma i) esto entraña: $Q=Q^\prime$. $\quad\Box$

Espacio vectorial como modelo de un espacio afín sobre sí mismo. Sea $E$ un espacio vectorial. Designamos por $\cal E$ otro ejemplar del propio $E$. Si $\vec u \in E$, designaremos por la correspondiente letra mayúscula, en este caso por $U$, el propio vector $\vec u$ considerado como elemento de $\cal E$. $\forall \, \vec u,\, \vec v \in E$ definimos:

$$\mbox{\fbox{${\displaystyle \overrightarrow {UV}= \colon \vec v - \vec u }$}}$$ (1)

Comprobemos los axiomas i), ii) y iii) para la aplicación $(U,V) \mapsto \overrightarrow {UV}$.

1. La relación $\overrightarrow {UV}=0$ significa $\vec v - \vec u =0$, equivalentemente $\vec u = \vec v$ o sea $U=V$.
2. Sean $U,V,W \in \cal E$. Tenemos:
   
   $$\overrightarrow {UV} + \overrightarrow {VW} = (\vec v - \vec u) + (\vec w - \vec v) = \vec w - \vec u = \overrightarrow {UW}$$
   
   

3. Sean $U \in {\cal E},\, \vec v \in E$. Definimos $\vec w = \colon \vec u + \vec v$. Con esto vale:
   
   $$\overrightarrow {UW}= \vec{w}- \vec u = \vec v$$
   
   

Así pues, mediante la definición 4.1.1, $\cal E$, es decir el propio $E$, es un espacio afín sobre sí mismo.

Gracias a esta observación, en todas las consideraciones donde entran a la vez espacios afines y espacios vectoriales, se puede, si conviene, mediante (1), considerarlos todos como espacios afines.

Definición 1.2  

1. Dados $P \in \cal E$ y $\vec u \in E$, el único punto $Q\in \cal E$ tal que $\overrightarrow {PQ}= \vec u$ se designa por:
   
   $$\fbox{${\displaystyle Q = \colon P + \vec u }$}$$
   
   

2. Sean $P,\, Q \in \cal E$. De conformidad con el convenio a) definimos:
   
   $$\fbox{${\displaystyle Q-P = \colon \overrightarrow {PQ} }$}$$
   
   

Vector posición

Fijemos un punto $I \in \cal E$ al que llamaremos ORIGEN. $\forall \, P \in \cal E$ el vector $\overrightarrow {IP}$ se llama el VECTOR POSICIÓN DEL PUNTO (CON RESPECTO AL ORIGEN ). Ocasionalmente designaremos este vector también por la notación

$${\cal V}_I(P)$$

Teorema 1.1   Para cualesquiera puntos $P,Q \in \cal E$ y cualquier origen $I$ vale:

$$\fbox{${\displaystyle \overrightarrow {PQ} = \overrightarrow {IQ}-\overrightarrow {IP}}$}$$

o sea, mediante la definición 4.1.2:

$$\fbox{${\displaystyle Q-P= \overrightarrow {IQ}-\overrightarrow {IP}}$}$$

o sea, todavía:

$$\fbox{${\displaystyle Q-P = {\cal V}_I(Q) - {\cal V}_I(P)}$}$$

Demostración
Por los enunciados ii) y $ii^\prime$) se cumple:

$$\overrightarrow {PQ}= \overrightarrow {PI} + \overrightarrow {IQ} = \overrightarrow {IQ}- \overrightarrow {IP}$$

$\quad\Box$

Corolario 1.1   Sean $P,\, Q \in \cal E$. Vale $P=Q$ si y sólo si (para algún origen I): $\overrightarrow {IP} = \overrightarrow {IQ}$.

Demostración
Por el teorema 4.1.1 la relación $\overrightarrow {IP} = \overrightarrow {IQ}$ implica $\overrightarrow {PQ} =0$ y ésta, a su vez, por el axioma i) de espacios afines $P=Q$. $\quad\Box$

Teorema 1.2   $\forall \, P \in {\cal E},\, \forall \, \vec u \in E$ vale para cualquier origen I:

$$\fbox{${\displaystyle {\cal V}_I (P + \vec u) = \overrightarrow {IP} + \vec u }$}$$

o sea,

$$\fbox{${\displaystyle {\cal V}_I (P + \vec u) = {\cal V}_I(P) + \vec u }$}$$

Demostración
Pongamos

$$P + \vec u = \colon Q$$ (2)

Debemos probar que:

$$\overrightarrow {IQ} = \overrightarrow {IP} + \vec u$$ (3)

Pero (2) significa $\vec u = \overrightarrow {PQ}$. Así pues, $\overrightarrow {IP} + \vec u = \overrightarrow {IP} + \overrightarrow {PQ}$ o sea, aplicando la relación de Chasles:

$$\overrightarrow {IP} + \vec{u}= \overrightarrow {IQ}$$

$\quad\Box$

Corolario 1.2   $\forall \, P \in {\cal E},\; \forall \, \vec u ,\, \vec v \in E$ vale:

$$\fbox{${\displaystyle {\cal V}_I (P + \vec u) - {\cal V}_I (P + \vec v) = \vec u - \vec v }$}$$

Observación
Las definiciones 4.1.2 introducen una convencional suma de un punto y de un vector y una, igualmente convencional, resta de dos puntos. Si combinamos estas nuevas ``operaciones'' con la adición y sustracción en $E$, ¿serían válidas las identidades que tales denominaciones implicarían?. Inesperadamente (salvo para un optimista empedernido): ¡sí!

Son ciertas, por ejemplo, las relaciones:

$$(P + \vec u ) + \vec v = P + ( \vec u + \vec v) , \quad P \in {\cal E};\, \vec u,\vec v \in E\quad \mbox{y}$$ (4)

$$(P + \vec u) - (Q+ \vec v) = (P-Q) + (\vec u - \vec v) \quad P,\, Q \in {\cal E}; \, \vec u, \vec v \in E$$ (5)

Los dos miembros de (4) son puntos. Para probar que son iguales, basta probar, en virtud del corolario del teorema 4.1.1, que tienen el mismo vector posición con respecto a algún origen $I$. Ahora bien, por el teorema 4.1.2 y la asociatividad de la adición en $E$:

$$\begin{eqnarray*} {\cal V}_I \left( (P + \vec u) + \vec v \right) &=& {\cal V}_I... ...ec u + \vec v)= {\cal V}_I \left( P + (\vec u + \vec v) \right) \end{eqnarray*}$$

Esto prueba (4).

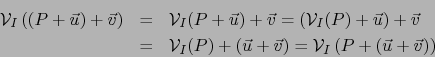
Los dos miembros de (5) son vectores. Aplicando los teoremas 4.1.1 y 4.1.2 obtenemos:

$$(P + \vec u) - (Q+ \vec v) = {\cal V}_I (P+ \vec u) - {\cal ... ...(P) + \vec u \right) - \left( {\cal V}_I (Q) + \vec v \right)$$ (6)

y, como todos los términos en el último miembro de (6) son vectores, se sigue de ahí, aplicando otra vez el teorema 4.1.1:

$$(P + \vec u) - (Q+ \vec v) = \left( {\cal V}_I (P) - {\cal V}_I (Q) \right) + (\vec u - \vec v) = (P-Q) + (\vec u - \vec v)$$

probando (5). $\quad\Box$

Nota
Comprobaciones como aquéllas en la observación precedente, aunque disipan las posibles dudas del lector, no quitan realmente el misterio del asunto. La verdadera explicación de éste estriba en que se puede construir un espacio vectorial $\overrightarrow {\cal E}$ que entre sus elementos tiene tanto todos los puntos de $\cal E$ como todos los vectores de $E$. Las operaciones introducidas por las definiciones 4.1.2 coinciden con las operaciones de la misma denominación en el espacio vectorial $\overrightarrow {\cal E}$ y el misterio se desvanece. De hecho, este espacio vectorial (los coautores del libro de L. SCHWARTZ [32] lo llaman el VECTORIALIZADO DEL ESPACIO AF´iN $\cal E$) permite un tratamiento sumamente elegante de la teoría de espacios afines: una completa ``linealización'' de ésta.

Como referencia me permito indicar al lector curioso [3]. No conozco nada sobre este tema que haya sido publicado por alguna casa editorial.

Teorema 1.3   Si $I$ es un origen arbitrario en $\cal E$, la aplicación:

$${\cal V}_I \colon P \mapsto \overrightarrow {IP}$$

es una biyección del espacio afín $\cal E$ sobre su espacio vectorial asociado E. La biyección inversa de E sobre $\cal E$ es:

$${\cal V}_I^{-1} \colon \vec u \mapsto I + \vec u$$

Demostración
El teorema se sigue inmediatamente de que, en virtud de los enunciados iii) y $iii^\prime$) para todo $\vec u \in E$ existe un único punto $P \in {\cal E}$ tal que $\overrightarrow {IP}= \vec u$. Según la definición 4.1.2, este punto no es otro que $P = I + \vec u$. $\quad\Box$

Definición 1.3   Sean $\cal E$ un espacio afín y E su espacio vectorial asociado.

1. Si el espacio vectorial E es de dimensión finita n, se dice que el espacio afín $\cal E$ es de DIMENSIÓN y se escribe $\mbox{\rm dim }{\cal E} =n$.
2. Si el espacio vectorial E es de dimensión infinita, se dice que el espacio afín $\cal E$ es de DIMENSIÓN INFINITA.

Definición 1.4   Si $\cal E$ es un espacio afín de dimensión finita n, se llama REFERENCIAL de $\cal E$ a una familia $(I;\vec{e}_1,\ldots,\vec{e}_n)$ donde I es un punto de $\cal E$ llamado ORIGEN DEL REFERENCIAL y $(\vec{e}_1,\ldots,\vec{e}_n)$ es una base del espacio vectorial E.

Teorema 1.4 (y definición)   Sean $\cal E$ un espacio afín de dimensión finita n e $(I;\vec{e}_1,\ldots,\vec{e}_n)$ un referencial de $\cal E$. La aplicación:

$$\mbox{\fbox{${\displaystyle (x^1,\ldots,x^n) \mapsto P=\colon I+ \sum_{i=1}^n x^i \vec{e}_i}$}}$$ (7)

es una biyección de ${\mathbb{K}}^n$ sobre $\cal E$.

Los escalares $x^1,\ldots,x^n$ en (7) se llaman las COORDENADAS DEL PUNTO CON RESPECTO AL REFERENCIAL $(I;\vec{e}_1,\ldots,\vec{e}_n)$.

La biyección inversa de la biyección (7) es

$$\mbox{\fbox{${\displaystyle P \mapsto \left(\pi^1(P),\ldots, \pi^n(P)\right)}$}}$$ (8)

donde:

$$\fbox{${\displaystyle \pi^i(P)= \colon \langle \overrightarro... ...5pt}}}}\limits \rangle \quad \mbox{ para }\quad i=1,\ldots,n}$}$$

siendo la base de $E^*$ dual de la base $(\vec{e}_1,\ldots,\vec{e}_n)$ de E.

Demostración
La aplicación (7) es la compuesta, en el orden que indicamos, de la biyección 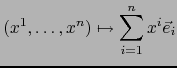${\displaystyle (x^1,\ldots,x^n) \mapsto \sum_{i=1}^n x^i \vec{e}_i }$ de ${\mathbb{K}}^n$ sobre $E$ con la biyección: ${\displaystyle {\cal V}_I^{-1} \colon \vec u \mapsto I+ \vec u}$ de $E$ sobre $\cal E$ del teorema 4.1.3. Por consiguiente, la aplicación (7) es una biyección de ${\mathbb{K}}^n$ sobre $\cal E$. $\quad\Box$

El estudio de las propiedades de $\cal E$ mediante tal biyección es la ``geometría analítica''.

Nota
En la terminología que usamos y que es la corriente entre los físicos, distinguimos cuidadosamente entre:

1. las ``componentes'' de un vector con respecto a una base y
2. las ``coordenadas'' de un punto con respecto a un referencial.

Cambio de referencial

Sean $(I;\vec{e}_1,\ldots,\vec{e}_n)$ un ``antiguo'' y $(J;\vec{f}_1,\ldots,\vec{f}_n)$ un ``nuevo'' referencial de $\cal E$. Para situar el nuevo referencial con respecto al antiguo damos las ``antiguas'' coordenadas $c^1,\ldots,c^n$ de $J$ y las componentes $a_k^i$ de $\vec{f}_k$ con respecto a la base $(\vec{e}_1,\ldots,\vec{e}_n)$. Tenemos pues:

$$\mbox{\fbox{${\displaystyle {\displaystyle J = I + \sum_{i=1}^n c^i \vec{e}_i}}$}}$$ (9)

y:

$$\mbox{\fbox{${\displaystyle \vec{f}_k = \sum_{i=1}^n a_k^i \vec{e}_i \quad \mbox{para} \;\; k=1,\ldots,n }$}}$$ (10)

Aquí $c^1,\ldots,c^n$ son elementos de ${\mathbb{K}}$ y $\left( a_k^i \right)_{1 \le k \le n}^{1\le i \le n}$ es una matriz $n\times n$ inversible de elementos en ${\mathbb{K}}$.

Sean $P$ un punto arbitrario de $\cal E$, $x^1,\ldots,x^n$ las antiguas e $y^1,\ldots,y^n$ las nuevas coordenadas de $P$. Vale pues:

$$M = I + \sum_{i=1}^n x^i \vec{e}_i = J + \sum_{k=1}^n y^k \vec{f}_k$$ (11)

Nos proponemos calcular las antiguas coordenadas $(x^1,\ldots,x^n)$ en fun-cinción de las nuevas $(y^1,\ldots,y^n)$. Usando las relaciones (11), (8) y (9) obtenemos:

$$I + \sum_{i=1}^n x^i \vec{e}_i = J+ \sum_{k=1}^n y^k \left( \sum_{i=1}^n a_k^i \vec{e}_i \right)$$

o sea:

$$I + \sum_{i=1}^n x^i \vec{e}_i = I + \sum_{i=1}^n \left( c^i + \sum_{k=1}^n a_k^i y^k \right) \vec{e}_i$$ (12)

Igualando los coeficientes de $\vec{e}_i$ en los dos miembros de (12) obtenemos finalmente:

$$\mbox{\fbox{${\displaystyle x^i = c^i + \sum_{k=1}^n a_k^i y^k\; ; \quad i=1,\ldots,n}$}}$$ (13)

(FÓRMULA DE CAMBIO DE COORDENADAS).

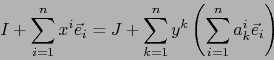
Esta fórmula es análoga a (14) del §5 del capítulo 2. para el cambio de componentes de un vector. Difiere de ella por la presencia del término ``constante'' $c^i$ en el segundo miembro.

Siguiente: Aplicaciones afines Arriba: Espacios afines Anterior: Espacios afines