




Siguiente: Semiespacios
Arriba: Espacios afines
Anterior: Primeras consecuencias de los
Debido a que, por el axioma iii) de espacios afines, todo vector de  puede expresarse (de muchas
maneras) en la forma
puede expresarse (de muchas
maneras) en la forma 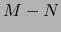 con
con
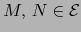 la aplicación lineal
la aplicación lineal  , si existe, es única. Se llama la PARTE LINEAL DE LA APLICACIÓN AF´iN
, si existe, es única. Se llama la PARTE LINEAL DE LA APLICACIÓN AF´iN 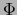 . La designaremos por la notación
. La designaremos por la notación 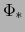 .
La fórmula (14) reza pues en definitiva:
.
La fórmula (14) reza pues en definitiva:
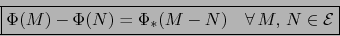 |
(15) |
O sea, al poner
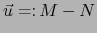 :
:
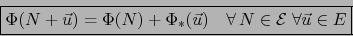 |
(16) |
El RANGO (finito o no) de la aplicación afín 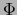 es, por definición, el rango de la
aplicación lineal
es, por definición, el rango de la
aplicación lineal 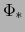 :
:
Demostración
- Unicidad.
- Supongamos que existe la aplicación afín deseada
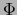 . Aplicando la fórmula (16) arriba con
. Aplicando la fórmula (16) arriba con 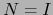 y teniendo
en cuenta la condición
y teniendo
en cuenta la condición 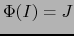 obtenemos la fórmula (17)
obtenemos la fórmula (17)
De esto se desprende que si 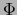 existe, es única.
existe, es única.
- Existencia.
- Definamos una aplicación
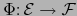 por la fórmula (17). Es claro que
por la fórmula (17). Es claro que 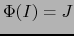 . Para dos puntos
arbitrarios
. Para dos puntos
arbitrarios
 vale (17) y
vale (17) y
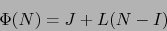 |
(19) |
Al restar (19) de (17) obtenemos:
Así pues,  es una aplicación afín
es una aplicación afín
 y
y  es su parte lineal.
es su parte lineal.

Observación
Sean  espacios vectoriales considerados, cada uno, como espacio afín sobre sí mismo como en la
observación después del enunciado
espacios vectoriales considerados, cada uno, como espacio afín sobre sí mismo como en la
observación después del enunciado  ) al comienzo de esta sección.
) al comienzo de esta sección.
Una aplicación
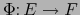 será una aplicación afín si y sólo si es de la forma:
será una aplicación afín si y sólo si es de la forma:
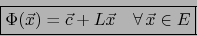 |
(20) |
donde 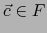 y
y  es una aplicación lineal de
es una aplicación lineal de  en
en  , o sea,
, o sea, 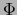 es la compuesta de
una aplicación lineal
es la compuesta de
una aplicación lineal 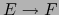 y de una traslación de
y de una traslación de  .
.
En esta situación 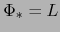 .
.
En efecto:
- De cumplirse (20), tenemos
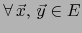 :
:
lo que prueba que 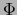 es una aplicación afín y
es una aplicación afín y  .
.
- Recíprocamente, sea
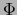 una aplicación afín
una aplicación afín 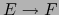 y sea
y sea
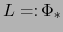 . Por la fórmula (17) del teorema 4.1.5 tenemos al escribir
. Por la fórmula (17) del teorema 4.1.5 tenemos al escribir
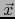 en vez de
en vez de  ,
, 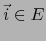 en vez de
en vez de 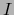 y
y 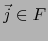 en vez de
en vez de  :
:
lo que es efectivamente de la forma (20).
Teorema 1.6
Sean  espacios afines sobre sendos espacios vectoriales
espacios afines sobre sendos espacios vectoriales 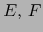 . Sea
. Sea
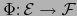 una aplicación afín.
una aplicación afín.
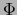 es inyectiva si y sólo si
es inyectiva si y sólo si 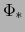 es una aplicación
lineal inyectiva
es una aplicación
lineal inyectiva 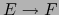 .
.
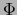 es superyectiva si y sólo si
es superyectiva si y sólo si 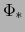 es una aplicación
lineal superyectiva
es una aplicación
lineal superyectiva 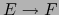 .
.
Demostración
- Escribamos:
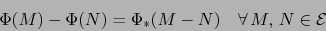 |
(21) |
Decir que 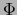 es una aplicación inyectiva, es decir que rige la
implicación:
es una aplicación inyectiva, es decir que rige la
implicación:
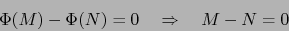 |
(22) |
Debido a (21), la implicación (22) equivale a la implicación:
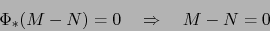 |
(23) |
Pero todo vector 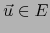 puede escribirse (de muchas maneras)
como una diferencia
puede escribirse (de muchas maneras)
como una diferencia 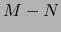 con
con
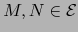 . Así pues, la
implicación (23) equivale a su vez a la implicación:
. Así pues, la
implicación (23) equivale a su vez a la implicación:
 |
(24) |
y (24) dice que la aplicación lineal 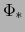 es inyectiva.
La equivalencia de las implicaciones (22) y (24) prueba, pues, la
afirmación a) del teorema.
es inyectiva.
La equivalencia de las implicaciones (22) y (24) prueba, pues, la
afirmación a) del teorema.
- Fijando arbitrariamente un punto
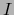 en
en  escribamos:
escribamos:
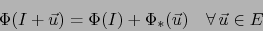 |
(25) |
(25) implica la relación:
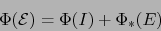 |
(26) |
(es decir
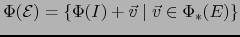 .)
De(26) se deduce que vale:
.)
De(26) se deduce que vale:
con lo cual viene probada la afirmación b) del teorema.

Demostración
-
 vale:
vale:
de donde la afirmación a).
- Con las notaciones de b) tenemos
 :
:
de donde la afirmación b).
- Sea
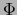 un isomorfismo afín de
un isomorfismo afín de  sobre
sobre 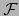 . Sean
. Sean 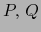 puntos arbitrarios
de
puntos arbitrarios
de 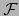 . Ponemos
. Ponemos
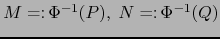 . La relación
. La relación
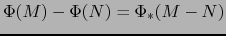 equivale
a:
equivale
a:
Esto prueba c). 
Observación (Expresiones analíticas en dimensión finita)
Sean  espacios afines y
espacios afines y
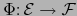 una aplicación afín.
una aplicación afín.
- Supongamos que el espacio afín
 es de dimensión finita
es de dimensión finita  y provisto
de un referencial
y provisto
de un referencial
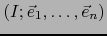 .
Para todo punto
.
Para todo punto
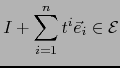 tenemos:
tenemos:
de donde, por linealidad de 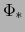 , finalmente:
, finalmente:
 |
(27) |
- Supongamos también
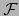 de dimensión finita
de dimensión finita  y provisto de un referencial
y provisto de un referencial
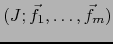 . Pongamos:
. Pongamos:
La matriz
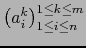 de tipo
de tipo 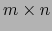 es la matriz
de la aplicación lineal
es la matriz
de la aplicación lineal
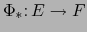 con respecto a las bases
con respecto a las bases
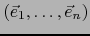 de
de
 y
y
 de
de  .
Llevando (28) y (29) al segundo miembro de (27), obtenemos:
.
Llevando (28) y (29) al segundo miembro de (27), obtenemos:
o sea,
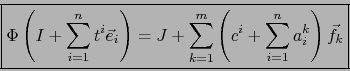 |
(30) |
La aplicación afín 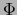 transforma, pues, el punto de coordenadas
transforma, pues, el punto de coordenadas
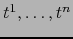 con
respecto al referencial
con
respecto al referencial
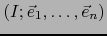 de
de  en el punto de coordenadas
en el punto de coordenadas
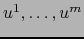 donde:
donde:
No es aquí el lugar para desarrollar la geometría afín propiamente dicha. Sin embargo,
hablaremos un poco de ``variedades afines''.
Observación
Sea dado un subespacio  de
de  . Para que un subconjunto no vacío
. Para que un subconjunto no vacío 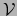 de
de  sea una variedad afín de dirección
sea una variedad afín de dirección  es necesario y suficiente que:
es necesario y suficiente que:
De esto se sigue sin más:
Definición 1.8
Sea  una parte no vacía cualquiera de
una parte no vacía cualquiera de  . Existen variedades afines en
. Existen variedades afines en
 que contienen a
que contienen a  : Por ejemplo,
: Por ejemplo,  entero es una de ellas. Por el
teorema 4.1.8, la intersección de todas las variedades afines en
entero es una de ellas. Por el
teorema 4.1.8, la intersección de todas las variedades afines en  que contienen
el conjunto
que contienen
el conjunto  es una variedad afín en
es una variedad afín en  .
Se llama la VARIEDAD AF´iN ENGENDRADA POR EL CONJUNTO
.
Se llama la VARIEDAD AF´iN ENGENDRADA POR EL CONJUNTO  .
.
Demostración
- Unicidad.
- Supongamos que existe una variedad afín
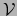 tal que
tal que 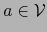 y
y
 .
En esta situación
.
En esta situación 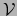 es un espacio afín sobre el espacio vectorial
es un espacio afín sobre el espacio vectorial  . Por el
teorema 4.1.3, la aplicación
. Por el
teorema 4.1.3, la aplicación
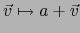 es una biyección de
es una biyección de  sobre
sobre
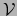 . Por lo tanto:
. Por lo tanto:
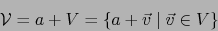 |
(31) |
de donde la unicidad de 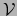 .
.
- Existencia.
Definimos un subconjunto
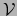 de
de  por la relación (31). Vale
por la relación (31). Vale
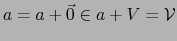 .
Resta probar que
.
Resta probar que 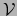 es una variedad afín de dirección
es una variedad afín de dirección  . Para ello, debemos
comprobar la validez de las reglas i) y ii) de la observación después de las definiciones 4.1.7.
. Para ello, debemos
comprobar la validez de las reglas i) y ii) de la observación después de las definiciones 4.1.7.
- i)
- Sean
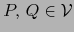 o sea
o sea
 con
con
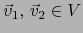 .
Se sigue
.
Se sigue
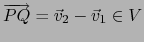 . Se cumple pues la regla i).
. Se cumple pues la regla i).
- ii)
- Sean
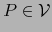 , o sea
, o sea
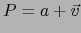 con
con 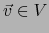 y sea
y sea 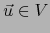 . Tenemos
. Tenemos
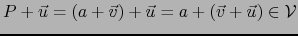 . Se cumple pues también la regla ii).
. Se cumple pues también la regla ii).

Corolario 1.4
Si 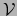 es una variedad afín en
es una variedad afín en  , por todo punto
, por todo punto 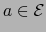 pasa una variedad afín y una sola
(de misma dimensión que
pasa una variedad afín y una sola
(de misma dimensión que 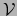 y) paralela a
y) paralela a 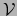 .
.
Se puede mirar este enunciado como un ``postulado de Euclides generalizado''.
Observación
Si 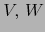 son subespacios de
son subespacios de  tales que
tales que  para las correspondientes variedades afines
para las correspondientes variedades afines  que
pasan por el punto
que
pasan por el punto 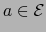 , vale:
, vale:
Lema 1.1
Sea
 un conjunto de
un conjunto de  punto de
punto de  . La variedad
afín engendrada por este conjunto es:
. La variedad
afín engendrada por este conjunto es:
Demostración
Sea  el subespacio
el subespacio
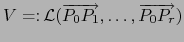 de
de  . Luego
. Luego
 . Por el teorema 4.1.9
. Por el teorema 4.1.9 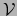 es una variedad afín. Al hacer
es una variedad afín. Al hacer
 en
la fórmula del enunciado se ve que
en
la fórmula del enunciado se ve que
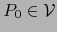 . Al hacer
. Al hacer 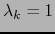 y
y 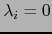 si
si 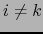 se ve que
se ve que
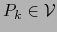 para
para 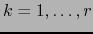 . Queda por probar que toda variedad afín
. Queda por probar que toda variedad afín 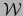 que
contiene
que
contiene
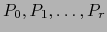 contiene
contiene 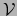 . Sea, pues,
. Sea, pues, 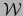 tal variedad afín y sea
tal variedad afín y sea
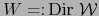 . Se puede escribir:
. Se puede escribir:
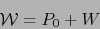 |
(32) |
De la regla i) de la observación después de las definiciones 4.1.7 se concluye que
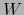 tiene como elementos los vectores
tiene como elementos los vectores
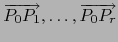 , de ahí que
, de ahí que 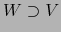 y,
por ende, de (32):
y,
por ende, de (32):
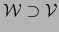 .
.

Sea 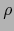 el rango del sistema
el rango del sistema
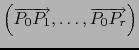 o sea
o sea
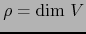 . Resulta de lo probado que el conjunto de puntos
. Resulta de lo probado que el conjunto de puntos
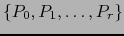 no está contenido
en ninguna variedad afín de dimensión menor que
no está contenido
en ninguna variedad afín de dimensión menor que 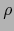 y que
y que 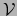 es la única variedad afín
de dimensión
es la única variedad afín
de dimensión 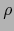 que contiene a dicho conjunto.
que contiene a dicho conjunto.
En efecto, si existe una variedad afín
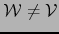 que la contiene, (32) implica que
que la contiene, (32) implica que 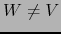 , luego
, luego
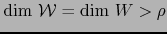 .
Sea dicho de paso que ni el subespacio
.
Sea dicho de paso que ni el subespacio  de
de  ni el rango del sistema
ni el rango del sistema
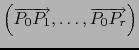 dependen
del orden de los puntos
dependen
del orden de los puntos
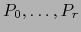 . Se puede, pues, sustituir
. Se puede, pues, sustituir 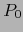 por cualquiera de los puntos
por cualquiera de los puntos
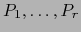 .
.
Teorema 1.10
Por  puntos
puntos
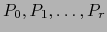 de
de  , que no pertenecen a una variedad afín de dimensión menor que
, que no pertenecen a una variedad afín de dimensión menor que
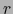 , pasa una y una sola variedad afín de
, pasa una y una sola variedad afín de  de dimensión
de dimensión 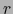 .
.
Demostración
- Si
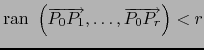 , por el lema 4.1.1
, por el lema 4.1.1
 y los puntos
y los puntos
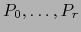 pertenecen a
pertenecen a  .
.
- Si
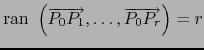 , por lo dicho arriba
, por lo dicho arriba
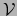 es la única variedad afín en
es la única variedad afín en  de dimensión
de dimensión 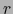 que contiene
al conjunto
que contiene
al conjunto
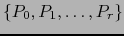 y ninguna variedad afín de dimensión menor que
y ninguna variedad afín de dimensión menor que 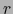 lo contiene.
lo contiene. 
Ejemplos
- Por dos puntos distintos de
 pasa una recta y una sola.
pasa una recta y una sola.
- Por tres puntos no colineales de
 (es decir, no situados en una recta) pasa
un plano y uno solo.
(es decir, no situados en una recta) pasa
un plano y uno solo.
Demostración
Sea 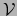 una variedad afín en
una variedad afín en  . Sea
. Sea
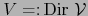 y sea
y sea 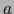 un punto de
un punto de 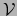 . La relación:
. La relación:
entraña:
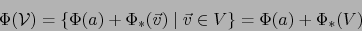 |
(33) |
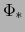 es una aplicación lineal del espacio vectorial
es una aplicación lineal del espacio vectorial  asociado con
asociado con  en el espacio
vectorial
en el espacio
vectorial  asociado con
asociado con 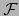 . Puesto que
. Puesto que  es un subespacio de
es un subespacio de  ,
, 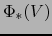 es un subespacio de
es un subespacio de  .
La fórmula (33) dice, pues, que
.
La fórmula (33) dice, pues, que
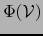 es una variedad afín de
es una variedad afín de 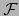 que pasa por el punto
que pasa por el punto
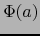 y tiene como dirección:
y tiene como dirección:






Siguiente: Semiespacios
Arriba: Espacios afines
Anterior: Primeras consecuencias de los
Guillermo M. Luna
2009-06-14
![]() puede expresarse (de muchas
maneras) en la forma
puede expresarse (de muchas
maneras) en la forma ![]() con
con
![]() la aplicación lineal
la aplicación lineal ![]() , si existe, es única. Se llama la PARTE LINEAL DE LA APLICACIÓN AF´iN
, si existe, es única. Se llama la PARTE LINEAL DE LA APLICACIÓN AF´iN ![]() . La designaremos por la notación
. La designaremos por la notación ![]() .
La fórmula (14) reza pues en definitiva:
.
La fórmula (14) reza pues en definitiva:
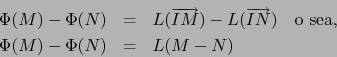
![]() espacios vectoriales considerados, cada uno, como espacio afín sobre sí mismo como en la
observación después del enunciado
espacios vectoriales considerados, cada uno, como espacio afín sobre sí mismo como en la
observación después del enunciado ![]() ) al comienzo de esta sección.
) al comienzo de esta sección.
![]() será una aplicación afín si y sólo si es de la forma:
será una aplicación afín si y sólo si es de la forma:
![]() .
.
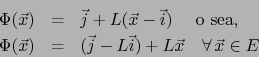
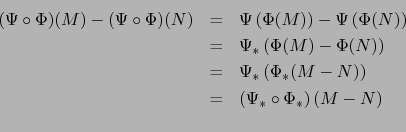

![]() espacios afines y
espacios afines y
![]() una aplicación afín.
una aplicación afín.
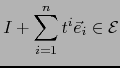 tenemos:
tenemos:
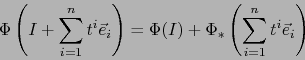
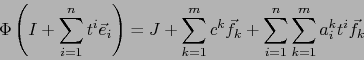
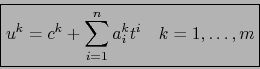
 , tal subespacio
, tal subespacio
![]() es un espacio afín de dimensión finita
es un espacio afín de dimensión finita ![]() , un hiperplano de
, un hiperplano de ![]() es simplemente
una variedad afín de dimensión
es simplemente
una variedad afín de dimensión ![]() en
en ![]() .
.
![]() mismo es siempre una variedad afín de
mismo es siempre una variedad afín de ![]() . Si
. Si ![]() es de dimensión finita
es de dimensión finita ![]() ,
, ![]() es la única variedad afín en
es la única variedad afín en ![]() de
dimensión
de
dimensión ![]() .
.
![]() de
de ![]() . Para que un subconjunto no vacío
. Para que un subconjunto no vacío ![]() de
de ![]() sea una variedad afín de dirección
sea una variedad afín de dirección ![]() es necesario y suficiente que:
es necesario y suficiente que:
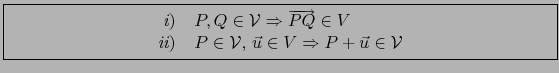
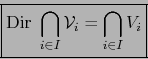
![]() son subespacios de
son subespacios de ![]() tales que
tales que ![]() para las correspondientes variedades afines
para las correspondientes variedades afines ![]() que
pasan por el punto
que
pasan por el punto ![]() , vale:
, vale:
![]() el subespacio
el subespacio
![]() de
de ![]() . Luego
. Luego
![]() . Por el teorema 4.1.9
. Por el teorema 4.1.9 ![]() es una variedad afín. Al hacer
es una variedad afín. Al hacer
![]() en
la fórmula del enunciado se ve que
en
la fórmula del enunciado se ve que
![]() . Al hacer
. Al hacer ![]() y
y ![]() si
si ![]() se ve que
se ve que
![]() para
para ![]() . Queda por probar que toda variedad afín
. Queda por probar que toda variedad afín ![]() que
contiene
que
contiene
![]() contiene
contiene ![]() . Sea, pues,
. Sea, pues, ![]() tal variedad afín y sea
tal variedad afín y sea
![]() . Se puede escribir:
. Se puede escribir:
![]() el rango del sistema
el rango del sistema
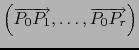 o sea
o sea
![]() . Resulta de lo probado que el conjunto de puntos
. Resulta de lo probado que el conjunto de puntos
![]() no está contenido
en ninguna variedad afín de dimensión menor que
no está contenido
en ninguna variedad afín de dimensión menor que ![]() y que
y que ![]() es la única variedad afín
de dimensión
es la única variedad afín
de dimensión ![]() que contiene a dicho conjunto.
que contiene a dicho conjunto.
![]() que la contiene, (32) implica que
que la contiene, (32) implica que ![]() , luego
, luego
![]() .
Sea dicho de paso que ni el subespacio
.
Sea dicho de paso que ni el subespacio ![]() de
de ![]() ni el rango del sistema
ni el rango del sistema
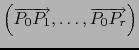 dependen
del orden de los puntos
dependen
del orden de los puntos
![]() . Se puede, pues, sustituir
. Se puede, pues, sustituir ![]() por cualquiera de los puntos
por cualquiera de los puntos
![]() .
.
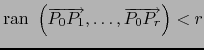 , por el lema 4.1.1
, por el lema 4.1.1
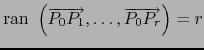 , por lo dicho arriba
, por lo dicho arriba
![]() una variedad afín en
una variedad afín en ![]() . Sea
. Sea
![]() y sea
y sea ![]() un punto de
un punto de ![]() . La relación:
. La relación: