Siguiente: Concepto de diferencial Arriba: Diferenciación en espacios afines Anterior: Diferenciación en espacios afines

Derivada según un vector

Sean ${\cal E},\, {\cal F}$ espacios afines normados sobre sendos espacios vectoriales $E$, $F$. Sea $\cal S$ un subconjunto de $\cal E$ y $\varphi$ una aplicación $\colon {\cal S} \to {\cal F}$. Describimos la situación abreviadamente por el simbolismo:

$${\cal E} \supset {\cal S} \mathop{\longrightarrow}\limits_{\varphi} {\cal F}$$

Sea a un punto interior de $\cal S$. Existe una bola $B(a,\rho)$ de $\cal E$ (bola abierta de centro $a$, de radio $\rho >0$) contenida en $\cal S$. Fijemos un vector arbitrario $\vec u$, no nulo, de $E$. Si $t \in {\mathbb{R}}$ satisface ${\displaystyle \vert t\vert < {\rho \over \Vert \vec u \Vert}}$, vale $a + t \vec u \in B(a,\rho) \subset \cal S$. De ahí se ve que la parte de ${\mathbb{R}}$:

$$T_{\vec u} = \colon \left\{ t \in {\mathbb{R}}\bigm\vert a + t\vec u \in {\cal S} \right\}$$

dominio de la aplicación $t \mapsto \varphi(a + t \vec u)$ tiene cero como punto interior. Adoptamos la definición:

$$\mbox{\fbox{${\displaystyle \partial_{\vec u} \varphi( a) = \... ... \ne 0} {\varphi(a + t \vec u) - \varphi(a) \over t} \in F}$}}$$ (1)

si el límite considerado existe. A continuación omitiremos la referencia explícita al conjunto $T_{\vec u}$.

El vector $\partial_{\vec u} \varphi(a)$ de $F$, si existe se llama la DERIVADA DE LA APLICACIÓN EN EL PUNTO SEGÚN EL VECTOR . En el caso particular de ser ${\cal E} = {\mathbb{R}}$ y $\vec u =1$, considerado como vector del espacio vectorial ${\mathbb{R}}$ de dimensión 1, se tiene $\partial_{\vec u} \varphi (a) = \varphi^\prime (a)$, la derivada usual de $\varphi$ en el punto $a$. Esta circunstancia motiva la definición (1).

La definición (1) conserva el sentido si $\vec u =0$. Por cierto la derivada según el vector cero siempre existe y se verifica:

$$\fbox{${\displaystyle \partial_0 \varphi(a) =0 \in F}$}$$

Supongamos que existe $\partial_{\vec u} \varphi(a)$. Fijemos $\lambda \in {\mathbb{R}}$ tal que $\lambda \ne 0$. Para $t \to 0$ el cociente: $\varphi ( a+t \lambda \vec u) - \varphi(a) \over t \lambda$ tiende a $\partial_{\vec u} \varphi(a)$ (pues $t \lambda \to 0$), pero también tiende a ${\displaystyle {1 \over \lambda} \partial_{\lambda \vec u} \varphi(a)}$.

Así pues: Si existe $\partial_{\vec u} \varphi(a)$, existe también $\partial_{\lambda \vec u} \varphi (a)$ y se verifica:

$$\mbox{\fbox{${\displaystyle \partial_{\lambda \vec u} \varphi (a) = \lambda \partial_{\vec u} \varphi (a)}$}}$$ (2)

Nota
Autores anglosajones dicen frecuentemente ``derivada direccional'' en vez de ``derivada según un vector''. La fórmula (2) muestra que esta terminología es incorrecta, pues si $\vec u \ne 0$, no es cierto que $\partial_{\vec u} \varphi(a)$ dependa solamente de la ``dirección'' de $\vec u$, o sea del subespacio ${\cal L}(\vec u)$ de $E$ de dimensión 1, engendrado por el vector $\vec u$.

Caso de ser $\cal E$ de dimensión finita

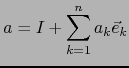Supongamos $\mbox{\rm dim }{\cal E} =n$ y consideremos una base $(\vec{e}_1,\ldots,\vec{e}_n)$ de $E$. Si para algún $i \in [\![ 1,n ]\!]$ existe la derivada $\partial_{\vec{e}_i} \varphi(a)$ la llamaremos DERIVADA PARCIAL DE EN , DE ´iNDICE CON RESPECTO A LA BASE #MATH4230#. Introduzcamos un ``origen'' $I \in \cal E$ y pongamos ${\displaystyle a= I + \sum_{k=1}^n a_k \vec{e}_k }$. Vale:

$$\begin{eqnarray*} \partial_{\vec{e}_i} \varphi (a) &=& \lim_{t \to 0 \atop t\ne ... ..._i\hspace{2em} \vec{e}_i + \cdots + a_n \vec{e}_n \right)\right] \end{eqnarray*}$$

De ahí vemos que si, mediante el referencial $(I;\vec{e}_1,\ldots,\vec{e}_n)$ identificamos los puntos de $\cal E$ con los correspondientes $n$-uplos de sus coordenadas, $\partial_{\vec{e}_i} \varphi(a)$ no será otra que la derivada parcial ``usual'' (de orden 1) de $\varphi$ en $a$ ``con respecto al argumento número $i$''.

Si mantenemos fija la base $(\vec{e}_1,\ldots,\vec{e}_n)$ nos permitiremos escribir simplemente $\partial_i \varphi(a)$ en vez de $\partial_{\vec{e}_i} \varphi(a)$. Esto será siempre el caso si ${\cal E}=E= {\mathbb{R}}^n$ y $(\vec{e}_1,\ldots,\vec{e}_n)$ es la base natural de ${\mathbb{R}}^n$.

En la última circunstancia $\partial_i \varphi(a)$ es sensu stricto la derivada parcial usual de $\varphi$ en $a$ ``con respecto al $i$-ésimo argumento''.

Nota
La existencia de las derivadas $\partial_{\vec u} \varphi(a)$ aun para todo $\vec u \in E$ (a fortiori la mera existencia de todas las derivadas parciales con respecto a una base en el caso de dimensión finita) no constituye todavía una generalización adecuada de la derivabilidad de $\varphi$ en $a$ en el caso familiar $\mbox{\rm dim } {\cal E}=1$, pues:

1. no implica la continuidad de $\varphi$ en $a$,
2. la aplicación $\vec u \mapsto \partial_{\vec u} \varphi (a)$ de $E$ en $F$ no es necesariamente lineal, como sería deseable,
3. aunque la condición se cumple para dos aplicaciones que se pueden componer, no se transmite en general a la aplicación compuesta.

La verdadera y fecunda generalización del concepto de derivada en dimensión 1 es aquél de ``diferencial'' que procedemos a definir.

Siguiente: Concepto de diferencial Arriba: Diferenciación en espacios afines Anterior: Diferenciación en espacios afines