




Siguiente: Diferenciales de funciones reales
Arriba: Diferenciación en espacios afines
Anterior: Derivada según un vector
Sea
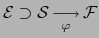 y sea
y sea 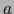 un punto interior de
un punto interior de 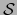 .
Ponemos
.
Ponemos
y consideramos
la aplicación
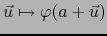 de
de 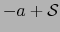 en
en 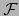 .
.
Sea 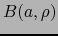 una bola abierta de
una bola abierta de  contenida en
contenida en 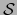 . Entonces
. Entonces
es una bola abierta de  de centro en 0,
contenida en
de centro en 0,
contenida en 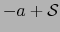 . El vector
. El vector 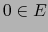 es pues un punto interior del conjunto
es pues un punto interior del conjunto 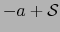 .
.
Sea
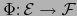 una aplicación afín continua. Deseamos que, en un sentido por
precisar,
una aplicación afín continua. Deseamos que, en un sentido por
precisar, 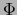 ``aproxime la aplicación
``aproxime la aplicación  cerca del punto
cerca del punto 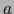 ''.
''.
En primer lugar exigimos:
 |
(3) |
Pedir luego que sea meramente
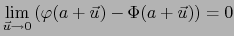 sería bien insuficiente, pues si
sería bien insuficiente, pues si  es continua en
es continua en 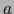 , esta condición se cumple para cualquier aplicación afín continua
, esta condición se cumple para cualquier aplicación afín continua 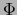 . En vez de lo último
requerimos pues que, cuando
. En vez de lo último
requerimos pues que, cuando 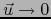 , la diferencia
, la diferencia
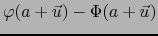 ``tienda a cero más
rápidamente que
``tienda a cero más
rápidamente que 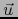 '' es decir:
'' es decir:
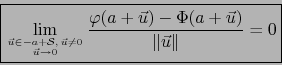 |
(4) |
Si se cumplen las relaciones (3) y (4), se dice que la aplicación afín continua 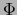 es TANGENTE A LA APLICACIÓN EN EL PUNTO .
es TANGENTE A LA APLICACIÓN EN EL PUNTO .
Mediante (3) vale:
luego (4) reza:
donde
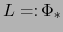 es una aplicación lineal continua
es una aplicación lineal continua 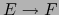 .
.
Estas consideraciones nos conducen a la siguiente:
Esta relación claramente equivale a:
Salvo cuando nos sea realmente útil, omitiremos en fórmulas de este tipo la referencia explícita al conjunto donde varía 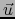 .
.
Teorema 3.1 (y definición)
La aplicación lineal continua
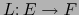 en la fórmula (5), si existe, es única. Se llama la DIFERENCIAL DE LA APLICACIÓN EN EL PUNTO y se le designa por
en la fórmula (5), si existe, es única. Se llama la DIFERENCIAL DE LA APLICACIÓN EN EL PUNTO y se le designa por 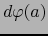 .
.
Existe, pues, entonces, una única aplicación afín continua
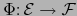 tangente a
tangente a  en el punto a. Está dada por:
en el punto a. Está dada por:
Demostración
Supongamos que existe  . Fijemos arbitrariamente un vector
. Fijemos arbitrariamente un vector  en
en  . Apliquemos la fórmula (5) al
vector
. Apliquemos la fórmula (5) al
vector
 con
con
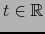 tal que
tal que
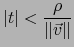 , lo que implica
, lo que implica
 . Obtenemos:
. Obtenemos:
Equivalentemente, al dividir el numerador y denominador por 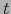 :
:
La última fórmula prueba que existe la derivada
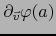 y vale:
y vale:
de donde la unicidad de  .
.

Observación 1
La fórmula (5) de la definición 4.2.3 se escribirá de aquí en adelante explícitamente:
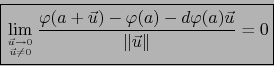 |
(6) |
Con más frecuencia escribiremos equivalentemente:
Existe una aplicación
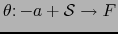 tal que:
tal que:
y
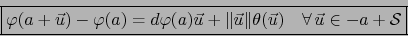 |
(7) |
Observación 2
La demostración del teorema 4.3.1 enseña lo siguiente:
Si  es diferenciable en el punto
es diferenciable en el punto 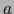 , para todo
, para todo 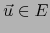 existe la derivada
existe la derivada
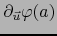 y vale
y vale
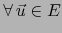 :
:
Así pues en este caso la aplicación
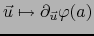 es una aplicación lineal
continua de
es una aplicación lineal
continua de  en
en  y, de hecho, coincide con la diferencial
y, de hecho, coincide con la diferencial 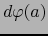 .
En particular si
.
En particular si  es de dimensión finita y
es de dimensión finita y
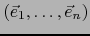 es una base de
es una base de  , obtenemos al poner:
, obtenemos al poner:
o sea
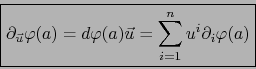 |
(8) |
donde
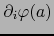 son las derivadas parciales de
son las derivadas parciales de  en
en 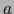 con respecto a la base
con respecto a la base
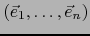 de E.
de E.
Observación 3
Sean
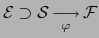 . Si
. Si  es una constante en
es una constante en  ,
,  es diferenciable en todo punto
interior p de
es diferenciable en todo punto
interior p de 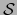 y para todo tal punto p:
y para todo tal punto p:
Demostración
Sea 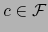 el valor constante de
el valor constante de  en
en 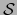 . La relación (7) de la
observación 1 es válida con
. La relación (7) de la
observación 1 es válida con
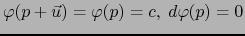 y
y 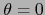 , de donde la
conclusión.
, de donde la
conclusión.
Observación 4 (Carácter local de la diferenciación)
Sean
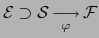 y
y 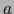 un punto interior de
un punto interior de 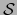 . Sea
. Sea 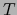 una parte de
una parte de 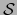 tal que
tal que
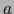 es también punto interior de
es también punto interior de 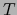 . La aplicación
. La aplicación  es diferenciable en el punto
es diferenciable en el punto
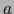 si y sólo si su restricción
si y sólo si su restricción  al conjunto
al conjunto 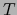 es diferenciable en el punto
es diferenciable en el punto 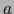 y entonces vale:
y entonces vale:
Demostración
Siendo 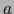 un punto interior de
un punto interior de 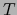 , existe
, existe
![$\rho^\prime \in ] 0,\rho ]$](img3252.png) tal que:
tal que:
Luego
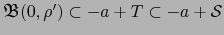 . Sea
. Sea  una aplicación
lineal continua de
una aplicación
lineal continua de  en
en  . Cada una de las relaciones:
. Cada una de las relaciones:
equivalen a:
Luego las relaciones (9) y (10) son equivalentes entre sí, de donde la conclusión. 
Teorema 3.2
Si la aplicación  es diferenciable en el punto
es diferenciable en el punto 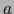 ,
,  es continua en
es continua en 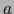 .
.
Se desprende, por ejemplo, de la fórmula (7) en la observación 1 arriba:

Teorema 3.3
El cambio de normas en  y
y  por sendas normas equivalentes no afecta ni la diferenciabilidad de
por sendas normas equivalentes no afecta ni la diferenciabilidad de  en el punto
en el punto
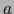 ni, en su caso, la diferencial
ni, en su caso, la diferencial 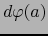 .
.
Demostración
Sean
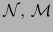 las ``antiguas'' y
las ``antiguas'' y
 las ``nuevas'' normas en
sendos espacios vectoriales
las ``nuevas'' normas en
sendos espacios vectoriales  ,
,  . Puesto que
. Puesto que
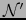 es equivalente a
es equivalente a  y
y
 es equivalente a
es equivalente a  , por el teorema 4.2.1 existen números positivos
, por el teorema 4.2.1 existen números positivos
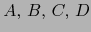 tales que:
tales que:
| |
|
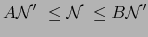 |
(11) |
| |
|
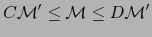 |
(12) |
Supongamos que para las antiguas normas
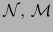 la aplicación
la aplicación  es diferenciable
en el punto
es diferenciable
en el punto 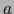 con la diferencial
con la diferencial 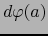 . Desde un principio notemos que
. Desde un principio notemos que 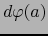 es también una aplicación lineal
continua de
es también una aplicación lineal
continua de  en
en  para las nuevas normas, pues éstas definen sobre sendos espacios
para las nuevas normas, pues éstas definen sobre sendos espacios  ,
,  las mismas
topologías que las antiguas. Por la fórmula (6) en la observación 1, después del teorema
4.3.1, nuestra hipótesis significa:
las mismas
topologías que las antiguas. Por la fórmula (6) en la observación 1, después del teorema
4.3.1, nuestra hipótesis significa:
Explícitamente, dado cualquier 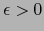 , existe
, existe  tal que:
tal que:
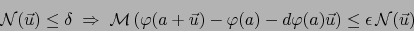 |
(13) |
Tomemos:
de donde por (11):
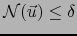 . De ahí , por la implicación (13) y la primera desigualdad en (12):
. De ahí , por la implicación (13) y la primera desigualdad en (12):
o sea, por la segunda desigualdad en (11):
Así viene probado que:
Luego  es diferenciable en el punto
es diferenciable en el punto 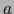 según las nuevas normas con la misma diferencial
según las nuevas normas con la misma diferencial 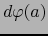 que con las antiguas.
que con las antiguas.

Este teorema dice esencialmente que la diferenciabilidad y la diferencial dependen no tanto de las normas individuales en  y
y  como
de las topologías que dichas normas inducen en sendos espacios
como
de las topologías que dichas normas inducen en sendos espacios  ,
, 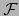 .
.
Consideremos el caso de ser  ,
, 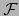 de dimensiones finitas. Sabemos por el teorema 4.2.15 que en el caso
considerado, las topologías tanto de
de dimensiones finitas. Sabemos por el teorema 4.2.15 que en el caso
considerado, las topologías tanto de  como de
como de 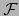 (que son las topologías ``naturales'' de estos espacios) no dependen de la elección de
las normas.
Al hacer el cálculo diferencial con espacios afines de dimensiones finitas es, pues, inútil precisar las normas que se usan en los correpondientes
espacios vectoriales asociados. Para resolver un problema particular se puede sin pérdida de generalidad trabajar con normas más cómodas para éste.
(que son las topologías ``naturales'' de estos espacios) no dependen de la elección de
las normas.
Al hacer el cálculo diferencial con espacios afines de dimensiones finitas es, pues, inútil precisar las normas que se usan en los correpondientes
espacios vectoriales asociados. Para resolver un problema particular se puede sin pérdida de generalidad trabajar con normas más cómodas para éste.
En el caso de ser  de dimensión finita, en virtud del teorema 4.2.6 sobra también el calificativo ``continua'' para la aplicación lineal
de dimensión finita, en virtud del teorema 4.2.6 sobra también el calificativo ``continua'' para la aplicación lineal
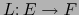 en la
definición de la diferenciabilidad.
en la
definición de la diferenciabilidad.
Demostración
Por la fórmula (5) después de la definición 4.1.5 vale
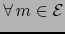 (resp.
(resp.
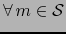 ) y
) y
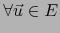 :
:
 |
(14) |
Por el teorema 4.2.19 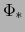 es una aplicación lineal continua:
es una aplicación lineal continua: 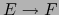 . Luego
la relación (14) es un caso particular de la relación (7) de la observación 1, después del teorema
4.3.1, con
. Luego
la relación (14) es un caso particular de la relación (7) de la observación 1, después del teorema
4.3.1, con 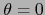 .
.
De ahí la conclusión.
En particular:
Si  es un abierto de
es un abierto de  vale:
vale:
Corolario 3.1 (del teorema
4.3.4.)
Sean  ,
,  espacios vectoriales normados y
espacios vectoriales normados y
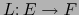 una aplicación lineal
continua (o la restricción de tal a un abierto S de E). Vale:
una aplicación lineal
continua (o la restricción de tal a un abierto S de E). Vale:
En efecto, según la observación después del teorema 4.1.5 y el teorema 4.1.7,  es un caso particular de una aplicación afín continua y
es un caso particular de una aplicación afín continua y  es su propia parte lineal.
es su propia parte lineal.





Siguiente: Diferenciales de funciones reales
Arriba: Diferenciación en espacios afines
Anterior: Derivada según un vector
Guillermo M. Luna
2009-06-14
![]() una bola abierta de
una bola abierta de ![]() contenida en
contenida en ![]() . Entonces
. Entonces
![]() una aplicación afín continua. Deseamos que, en un sentido por
precisar,
una aplicación afín continua. Deseamos que, en un sentido por
precisar, ![]() ``aproxime la aplicación
``aproxime la aplicación ![]() cerca del punto
cerca del punto ![]() ''.
''.

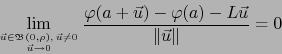
![]() tangente a
tangente a ![]() en el punto a. Está dada por:
en el punto a. Está dada por:
![]() . Fijemos arbitrariamente un vector
. Fijemos arbitrariamente un vector ![]() en
en ![]() . Apliquemos la fórmula (5) al
vector
. Apliquemos la fórmula (5) al
vector
![]() con
con
![]() tal que
tal que
![]() , lo que implica
, lo que implica
![]() . Obtenemos:
. Obtenemos:

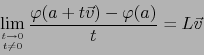
![]() es diferenciable en el punto
es diferenciable en el punto ![]() , para todo
, para todo ![]() existe la derivada
existe la derivada
![]() y vale
y vale
![]() :
:

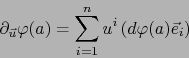
![]() . Si
. Si ![]() es una constante en
es una constante en ![]() ,
, ![]() es diferenciable en todo punto
interior p de
es diferenciable en todo punto
interior p de ![]() y para todo tal punto p:
y para todo tal punto p:
![]() el valor constante de
el valor constante de ![]() en
en ![]() . La relación (7) de la
observación 1 es válida con
. La relación (7) de la
observación 1 es válida con
![]() y
y ![]() , de donde la
conclusión.
, de donde la
conclusión.
![]() y
y ![]() un punto interior de
un punto interior de ![]() . Sea
. Sea ![]() una parte de
una parte de ![]() tal que
tal que
![]() es también punto interior de
es también punto interior de ![]() . La aplicación
. La aplicación ![]() es diferenciable en el punto
es diferenciable en el punto
![]() si y sólo si su restricción
si y sólo si su restricción ![]() al conjunto
al conjunto ![]() es diferenciable en el punto
es diferenciable en el punto ![]() y entonces vale:
y entonces vale:
![]() un punto interior de
un punto interior de ![]() , existe
, existe
![]() tal que:
tal que:

![]() las ``antiguas'' y
las ``antiguas'' y
![]() las ``nuevas'' normas en
sendos espacios vectoriales
las ``nuevas'' normas en
sendos espacios vectoriales ![]() ,
, ![]() . Puesto que
. Puesto que
![]() es equivalente a
es equivalente a ![]() y
y
![]() es equivalente a
es equivalente a ![]() , por el teorema 4.2.1 existen números positivos
, por el teorema 4.2.1 existen números positivos
![]() tales que:
tales que:

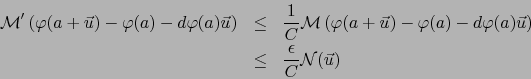
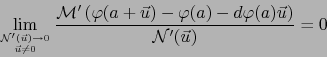
![]() y
y ![]() como
de las topologías que dichas normas inducen en sendos espacios
como
de las topologías que dichas normas inducen en sendos espacios ![]() ,
, ![]() .
.
![]() ,
, ![]() de dimensiones finitas. Sabemos por el teorema 4.2.15 que en el caso
considerado, las topologías tanto de
de dimensiones finitas. Sabemos por el teorema 4.2.15 que en el caso
considerado, las topologías tanto de ![]() como de
como de ![]() (que son las topologías ``naturales'' de estos espacios) no dependen de la elección de
las normas.
Al hacer el cálculo diferencial con espacios afines de dimensiones finitas es, pues, inútil precisar las normas que se usan en los correpondientes
espacios vectoriales asociados. Para resolver un problema particular se puede sin pérdida de generalidad trabajar con normas más cómodas para éste.
(que son las topologías ``naturales'' de estos espacios) no dependen de la elección de
las normas.
Al hacer el cálculo diferencial con espacios afines de dimensiones finitas es, pues, inútil precisar las normas que se usan en los correpondientes
espacios vectoriales asociados. Para resolver un problema particular se puede sin pérdida de generalidad trabajar con normas más cómodas para éste.
![]() de dimensión finita, en virtud del teorema 4.2.6 sobra también el calificativo ``continua'' para la aplicación lineal
de dimensión finita, en virtud del teorema 4.2.6 sobra también el calificativo ``continua'' para la aplicación lineal
![]() en la
definición de la diferenciabilidad.
en la
definición de la diferenciabilidad.
![]() (resp.
(resp.
![]() ) y
) y
![]() :
:
![]() es un abierto de
es un abierto de ![]() vale:
vale: