Posterior: Barbara Arriba: Deducción natural en el Anterior: Deducción natural en el

Silogística

La TEOR´iA TRADICIONAL DEL SILOGISMO trata de fórmulas correspondientes a los esquemas siguientes:

A (Universal afirmativa).

``Todo $S$ es $P$''

E (Universal negativa).

``Ningún $S$ es $P$''

I (Existencial afirmativa).

``Algún $S$ es $P$''

O (Existencial negativa).

``Algún $S$ no es $P$''

Las letras designativas fueron elegidas así porque las correspondientes a las afirmaciones aparecen en la palabra latina AffIrmo y las negativas en nEgO. Así pues, como fórmulas bien formadas, estos esquemas quedan:

$$\begin{array}{ccl@{\hspace{1cm}}ccl} A&:& \forall x\,\left(S... ... \exists x\,\left(S(x)\land \neg P(x)\right) %%\\ \end{array}$$

En estos esquemas, el predicado $S(x)$ se llama SUJETO y $P(x)$ COMPLEMENTO. Un SILOGISMO consiste de dos PREMISAS y de una CONCLUSIÓN. Ambas premisas contienen un predicado común, que no aparece en la conclusión, la cual ha de ser una consecuencia lógica de las premisas. El sujeto de la conclusión es el TÉRMINO MENOR del silogismo, el complemento de la conclusión es el TÉRMINO MAYOR y el predicado común a las premisas es el TÉRMINO MEDIO. Por la colocación de los términos menor, medio y mayor, los silogismos se clasifican en cuatro FIGURAS, las cuales se bosquejan en la tabla 3.5.

Table 3.5: Las cuatro figuras del silogismo tradicional.

$M$ - $P$ $S$ - $M$ $S$ - $P$ Figura 1	$P$ - $M$ $S$ - $M$ $S$ - $P$ Figura 2
$M$ - $P$ $M$ - $S$ $S$ - $P$ Figura 3	$P$ - $M$ $M$ - $S$ $S$ - $P$ Figura 4

$S$: Término menor. $M$: Término medio. $P$: Término mayor.

Ahora bien, atendiendo a los esquemas de las premisas y de la conclusión, los silogismos se clasifican en MODOS. En principio, podría formarse hasta $4^3=2^6=64$ modos distintos, los que multiplicados por las 4 figuras proporcionarían hasta $4\cdot 4^3=2^8=256$ silogismos posibles. Sin embargo, es bien sabido que sólo 24 silogismos son lógicamente válidos. Cada silogismo válido se identifica con una palabra mnemotécnica que es un nombre latino, y esta convención se remonta a la Edad Media. En cada nombre, la primera vocal indica el esquema de la primera premisa, la segunda vocal el de la segunda premisa y la tercera vocal el de la conclusión. Hay cuatro silogismos correctos correspondientes a la primera figura, cuatro a la segunda, seis a la tercera y cinco a la cuarta. Estos dan diecinueve silogismos en los que la conclusión está cuantificada universalmente. Los cinco silogismos restantes son versiones existenciales en la conclusión de cinco anteriores. Los diecinueve primeros silogismos correctos aparecen clasificados por figuras en los siguientes versos latinos:

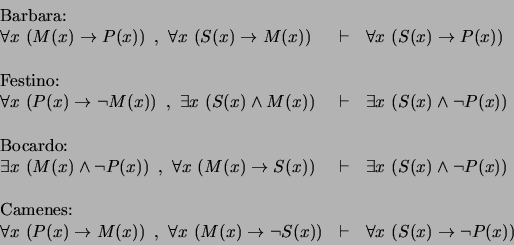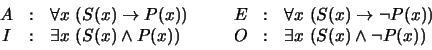
Barbara, Celarent, Darii, Ferioque prioris;
Cesare, Camestres, Festino, Baroco secundæ;
tertia Darapti, Disamis, Datisi, Felapton;
Bocardo, Ferison habet. Quarta insuper addit
Bramantip, Camenes, Dimaris, Fesapo, Fresison.

Los cinco modos restantes son Barbari y Celaront en la figura 1, Cesaro y Camestrop en la figura 2 y Camenop en la figura 4. Por si fuera poco el ingenio de quienes asignaron estos nombres, se tiene que las consonantes en cada nombre son también claves mnemotécnicas para transformar silogismos de las demás figuras en correspondientes silogismos equivalentes de la figura 1 (obsérvese que todos los nombres comienzan sólo con B, C, D y F). Como meros ejemplos, formalicemos en el cálculo de predicados a un silogismo de cada una de las cuatro figuras. Consideremos pues:

$$\begin{array}{lcl} \mbox{\rm Barbara:} & & \\ \forall x\,\... ...left(S(x)\rightarrow \neg P(x)\right) %%\\ & & \\ \end{array}$$

Veamos cómo construir una prueba de cada uno de ellos en el cálculo de predicados.

Posterior: Barbara Arriba: Deducción natural en el Anterior: Deducción natural en el