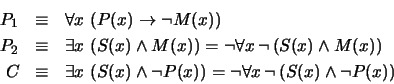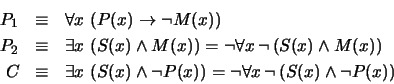Posterior: Bocardo
Arriba: Silogística
Anterior: Barbara
Para demostrar la validez de este silogismo, escribamos:
Por Barbara se tiene
o equivalentemente
o sea
Por el Teorema de Deducción:
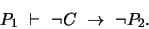 |
(5) |
Por otro lado, se tiene como un teorema
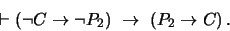 |
(6) |
Así pues, de (5) y (6) por Modus Ponens resulta
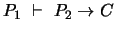 , de lo cual el Teorema de Deducción da, finalmente, el esquema Festino:
, de lo cual el Teorema de Deducción da, finalmente, el esquema Festino:
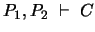 .
. 
Guillermo Morales-Luna
2004-07-27