| (6) |
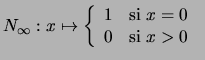
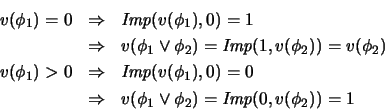
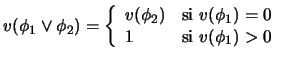 En consecuencia, la disyunción puede
no ser conmutativa.
Es menester pues introducir de alguna otra forma a los
conectivos.
Dado un operador conjuntor que ``no tenga saltos'' es posible reconstruir
a los operadores Máximo y Mínimo. La demostración es puramente
técnica (consiste de hecho en la comprobación de algunas
desigualdades) y por eso la omitimos:
En consecuencia, la disyunción puede
no ser conmutativa.
Es menester pues introducir de alguna otra forma a los
conectivos.
Dado un operador conjuntor que ``no tenga saltos'' es posible reconstruir
a los operadores Máximo y Mínimo. La demostración es puramente
técnica (consiste de hecho en la comprobación de algunas
desigualdades) y por eso la omitimos:
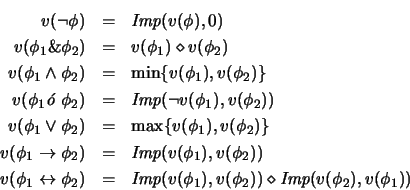
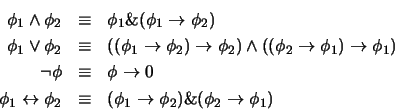
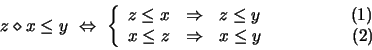
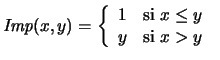 Los valores de verdad de los conectivos quedan entonces definidos como en
el recuadro (4.11),
Los valores de verdad de los conectivos quedan entonces definidos como en
el recuadro (4.11), 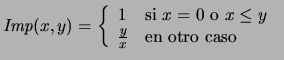 Los valores de verdad de los conectivos quedan entonces definidos como en
el recuadro (4.12),
Los valores de verdad de los conectivos quedan entonces definidos como en
el recuadro (4.12),