
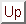

Posterior: Problemas típicos de lógicas
Arriba: Lógicas proposicionales difusas
Anterior: Semánticas basadas en conjunción
Hasta ahora hemos extendido los conectivos siguiendo principalmente dos
enfoques: En uno consideramos una conjunción y una negación como
básicos. En otro, consideramos una conjunción, en términos de ella
definimos una implicación, y estos dos conectivos fueron considerados
para ser los básicos.
Para finalizar las posibles extensiones de asignaciones, supongamos dadas
una implicación
![$\mbox{\it Imp}:[0,1]^2\rightarrow[0,1]$](img356.png) y una negación
y una negación
![$N:[0,1]\rightarrow[0,1]$](img259.png) como conectivos básicos. Entonces podemos extender
valores de verdad a los demás conectivos como sigue:
como conectivos básicos. Entonces podemos extender
valores de verdad a los demás conectivos como sigue:
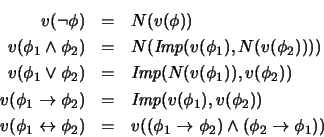
Veamos algunos
ejemplos. En todos ellos supondremos que la negación es
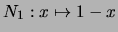 .
.
- Producto-D.
- Para la función
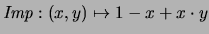 obtenemos los mismos operadores que
en el caso Producto-D definido anteriormente.
obtenemos los mismos operadores que
en el caso Producto-D definido anteriormente.
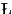 ukasiewicz-D.
ukasiewicz-D.- Para
la función
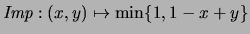 obtenemos los
mismos operadores que en el caso
obtenemos los
mismos operadores que en el caso 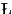 ukasiewicz-D definido anteriormente.
ukasiewicz-D definido anteriormente.
- Implicación por inclusión.
- Consideremos
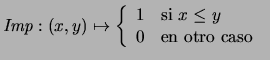 Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.14).
Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.14).
Table 4.14:
Conectivos resultantes de la
implicación por inclusión.
![\begin{table}
\begin{center}\fbox{\begin{minipage}[t]{30em} \begin{eqnarray*}
...
...end{array}\right. %%\\
\end{eqnarray*}
\end{minipage}}\end{center} \end{table}](img406.png) |
- Implicación de Brower o por falla.
- Consideremos
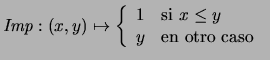 Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.15).
Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.15).
Table 4.15:
Conectivos resultantes de la
implicación de Brower.
![\begin{table}
\begin{center}\fbox{\begin{minipage}[t]{30em} \begin{eqnarray*}
...
...t=0 . \end{array}\right. \end{eqnarray*}
\end{minipage}}\end{center} \end{table}](img408.png) |
En este caso, ni la
conjunción ni la disyunción son conmutativas.
- Implicación de
Zadeh.
- Consideremos
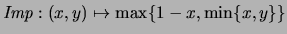 Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.16).
Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.16).
Table 4.16:
Conectivos resultantes de la
implicación de Zadeh.
![\begin{table}
\begin{center}\fbox{\begin{minipage}[t]{33em} \begin{eqnarray*}
...
...> 1]. \end{array}\right. \end{eqnarray*}
\end{minipage}}\end{center} \end{table}](img410.png) |
En este caso, ni la
conjunción ni la disyunción son conmutativas.
- Implicación de
Bayes.
- Consideremos
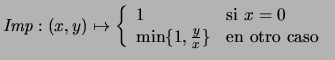 Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.17).
Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.17).
Table 4.17:
Conectivos resultantes de la
implicación de Bayes.
![\begin{table}
\begin{center}\fbox{\begin{minipage}[t]{30em} \begin{eqnarray*}
...
...i_2). \end{array}\right. \end{eqnarray*}
\end{minipage}}\end{center} \end{table}](img412.png) |
En este caso, ni la
conjunción ni la disyunción son conmutativas.


Posterior: Problemas típicos de lógicas
Arriba: Lógicas proposicionales difusas
Anterior: Semánticas basadas en conjunción
Guillermo Morales-Luna
2004-07-28
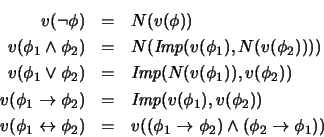
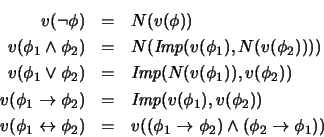
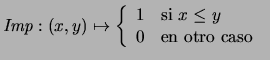 Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.14).
Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.14). 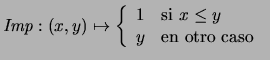 Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.15).
Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.15). 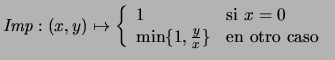 Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.17).
Se tiene que los conectivos tendrán las funciones mostradas en el
recuadro (4.17).