| = | (327) |
The Schrödinger equation for a linear potential has Airy functions as its solution. One of its interesting properties is that a translation of the origin can be compensated by a shift in energy level, so that in principle the solutions for any one energy suffice for all. The equation is
| = | (327) |
| (328) |
![$\displaystyle \begin{array}{ccc}
P & = & \frac{1}{\surd2}
\left[ \begin{array}{cc} \lambda & -\lambda \\ 1 & 1 \end{array} \right], \end{array}$](img531.gif) |
![$\displaystyle \begin{array}{ccc}
P^{-1} & = & \frac{1}{\surd2}
\left[ \begin{array}{cc} 1/\lambda & 1 \\ -1/\lambda & 1 \end{array} \right]. \end{array}$](img532.gif) |
(329) |
With this preparation, the WKB factorization embodied in equation (266) can be applied. We need the integrated eigenvalue to produces an angle
| = | 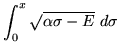 |
(330) | |
| = |  |
(331) |
At first appearance, the solution of the Airy equation would be
| Z(x) | = | ![$\displaystyle \frac{1}{\lambda^2} \left[ \begin{array}{cc}
\cos(\phi) & -\sin(\phi) \\ \sin(\phi) & \cos(\phi)
\end{array} \right],$](img537.gif) |
(332) |
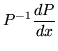 |
= | ![$\displaystyle \frac{\alpha}{4\lambda^2}
\left[ \begin{array}{cc} 1 & -1 \\ -1 & 1 \end{array} \right],$](img539.gif) |
(333) |
| = | 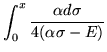 |
(334) | |
| = | (335) |
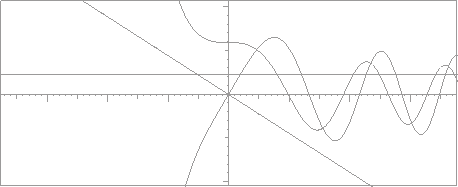 |
Figure 19 shows the result of a numerical integration of the Airy equation, choosing the two basic solutions as the one similar to a sine (initial value 0, derivative 1) together with the one similar to a cosine (initial value 1, derivative 0).
Of course, calculating the exponential of a logarithm gives the argument back, which is a way to avoid the singularity implied by the logarithm. It would be more in keeping with the spirit of complex variable theory to give the energy a small imaginary component, replacing E by
![]() ,
and narrowly avoiding the singularity. The main preoccupation is to get the trigonometrric functions on one side of the singularity to connect smoothly with the hyperbolic functions on the other side.
,
and narrowly avoiding the singularity. The main preoccupation is to get the trigonometrric functions on one side of the singularity to connect smoothly with the hyperbolic functions on the other side.
Splitting the coefficent matrix for the Schrödinger equation has mainly historical interest, given the ease of performing numerical integrations nowadays. Nevertheless, it is often useful to have an approximation in terms of more ordinary functions, either for symbolic calculations or as a starting point for mixed numerical computations.
Figure 20 shows the same result in the phase plane, which is the natural domain of the Prüfer transformation.