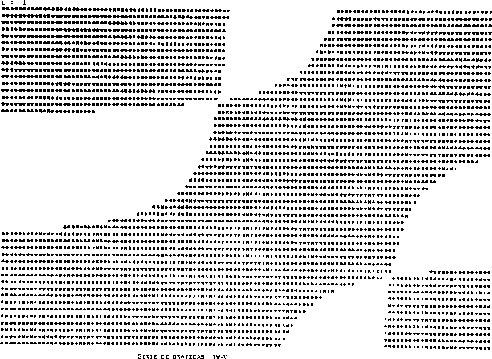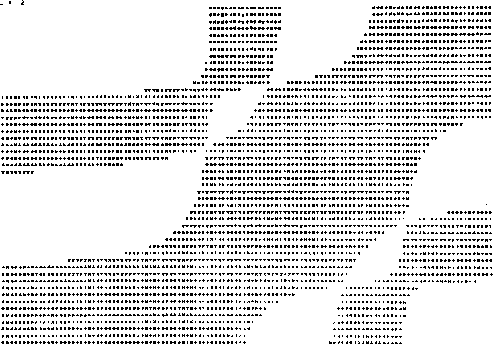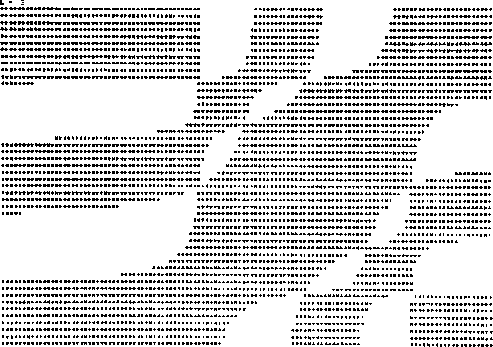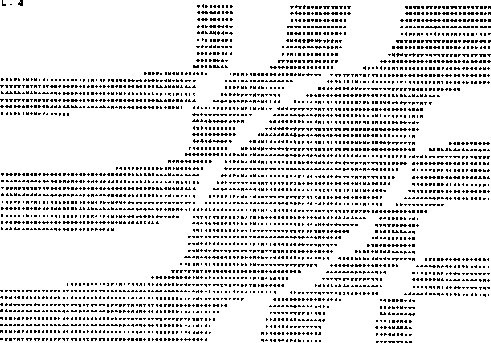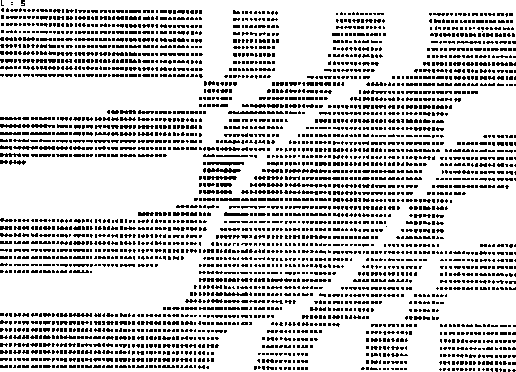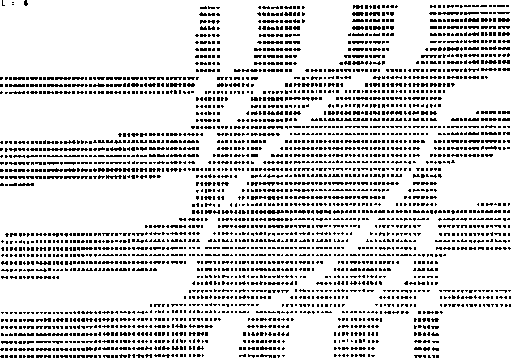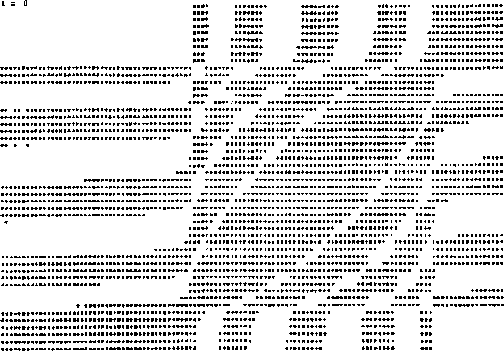Por lo tanto lo que queremos evaluar es la forma explícita de la
ecuación de eigenvalores, para lo cual es necesario el cálculo de
los elementos de la matriz ![]() . Empleando la notación
usada para deducir la ecuación (3.14) esto es:
. Empleando la notación
usada para deducir la ecuación (3.14) esto es:
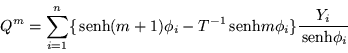
Para el caso de vibraciones a segundos vecinos, únicamente
vamos a tener el desarrollo para dos términos, como vimos
anteriormente por lo tanto de la fórmula para ![]() .
.
![$\displaystyle \frac{[\cosh\Phi -II\cosh\phi_2 ]}
{[\cosh\phi_1 -\cosh\phi_2 ]}$](img553.gif) |
|||
| (4.44) | |||
![$\displaystyle \frac{[\cosh\Phi -II\cosh\phi_1 ]}
{[\cosh\phi_1 -\cosh\phi_2 ]}$](img555.gif) |
Además habíamos definido anteriormente (ec. 3.14)
que
![\begin{displaymath}
\cosh\Phi =\frac{1}{2} \left[\begin{array}{rccr}
\gamma &...
...& 1 \\
-1 & \gamma & \beta +1 & \gamma
\end{array}\right]
\end{displaymath}](img557.gif)
Por lo tanto los operadores de proyección ![]() y
y ![]() quedan
finalmente como
quedan
finalmente como
![\begin{eqnarray*}
\gamma _1 & = & \frac{1}{\cosh\phi_1 -\cosh\phi_2} \left[\begi...
...\cosh\phi_2 & \cosh\phi_2
\end{array}\right] %% linea de \beas
\end{eqnarray*}](img559.gif)
Si sustituimos en la ecuación (4.43) la forma
matricial de los operadores ![]() y
y ![]() junto con las ecuaciones
dadas por (4.42), obtendremos finalmente
junto con las ecuaciones
dadas por (4.42), obtendremos finalmente ![]() y por lo
consiguiente la forma explícita de la ecuación de eigenvalores,
que está dada por el menor de la matriz
y por lo
consiguiente la forma explícita de la ecuación de eigenvalores,
que está dada por el menor de la matriz ![]() , con objeto de
reducir el álgebra escribiremos únicamente el cofactor
, con objeto de
reducir el álgebra escribiremos únicamente el cofactor ![]() de
la esquina superior izquierda, esto es:
de
la esquina superior izquierda, esto es:
![\begin{displaymath}
\cdot \left[\begin{array}{ccc}
\,{\mbox{senh}}(m+1)\phi_1 \...
...ts & \vdots \\
\cdots & \cdots & \vdots
\end{array}\right] + \end{displaymath}](img562.gif)
![\begin{displaymath}
\cdot \left[\begin{array}{ccc}
\,{\mbox{senh}}(m+1)\phi_2 \...
...ts \\ %% Reng. 3
\cdots & \cdots & \cdots
\end{array}\right] \end{displaymath}](img564.gif) |
(4.45) |
Por lo tanto tenemos finalmente los elementos del menor
![]() los cuales son:
los cuales son:
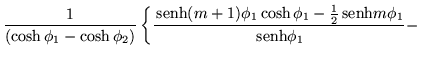 |
|||
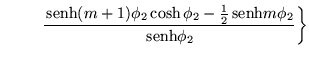 |
|||
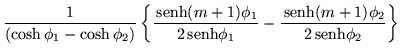 |
|||
| (4.46) | |||
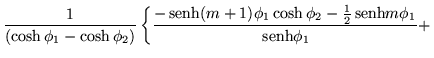 |
|||
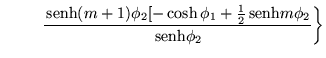 |
|||
![$\displaystyle \frac{1}{(\cosh\phi_1 -\cosh\phi_2)}\left\{
\frac{\,{\mbox{senh}}...
...sh\phi_2]
+\,{\mbox{senh}}m\phi_1\cosh\phi_2}
{\,{\mbox{senh}}\phi_1} + \right.$](img575.gif) |
|||
![$\displaystyle \left. \qquad
\frac{-\,{\mbox{senh}}(m+1)\phi_2[-\frac{1}{2}-2\co...
...cosh\phi_2]
-\,{\mbox{senh}}m\phi_2\cosh\phi_1}
{\,{\mbox{senh}}\phi_2}\right\}$](img576.gif) |
Después de cierta álgebra considerable, (ver apéndice C),
obtenemos que el espectro de eigenvalores para el interior de
cualquier cadena y en partícular para una cadena con extremos
fijos, que se puede considerar como el interior de una cadena, esta
dado por la ecuación determinantal.
| (4.47) |
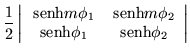 |
(4.48) | ||
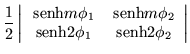 |
(4.49) |
Además un denominador opcional,
![]() es disponible.
es disponible.
Si consideramos
![]() junto con los
polinomios de Tchebychev dados por
junto con los
polinomios de Tchebychev dados por
![]() (en donde si
(en donde si ![]() es un ángulo tal que
es un ángulo tal que
![]() , entonces
, entonces ![]() tiene la
forma
tiene la
forma ![]() ó
ó ![]() , nosotros podemos emplear la misma
notación, desde luego
, nosotros podemos emplear la misma
notación, desde luego
![]() ,
y los factores
,
y los factores ![]() se cancelan de la ecuación
se cancelan de la ecuación
![]() ,
resulta después de cierta álgebra (ver apéndice D) que
,
resulta después de cierta álgebra (ver apéndice D) que
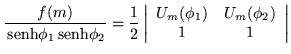 |
|||
| (4.50) | |||
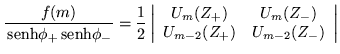 |
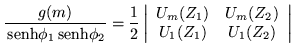 |
|||
| (4.51) | |||
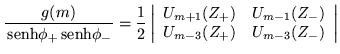 |
Que es precisamente en términos de estas ecuaciones, como se graficó
el espectro de eigenvalores dado por la condición de que
![]() como se
puede apreciar en la gráfica (IV.V). En esta gráfica se varió
como se
puede apreciar en la gráfica (IV.V). En esta gráfica se varió ![]() y
y
![]() fijando el valor de
fijando el valor de ![]() , por lo cual se obtienen contornos de regiones
negativas (región estrellada) y positivas (región blanca), en donde la
frontera de estas dos regiones nos da la variación de las frecuencias. Esta
gráfica como se puede apreciar fácilmente se realizó en un sistema de
coordenadas distinto al de la gráfica (IV.IV), pero nos representa la misma
informacion. En el apéndice D se da un ejemplo para
, por lo cual se obtienen contornos de regiones
negativas (región estrellada) y positivas (región blanca), en donde la
frontera de estas dos regiones nos da la variación de las frecuencias. Esta
gráfica como se puede apreciar fácilmente se realizó en un sistema de
coordenadas distinto al de la gráfica (IV.IV), pero nos representa la misma
informacion. En el apéndice D se da un ejemplo para ![]() y se obtiene
la forma explícita del determinante que se empleó para graficar los
polinomios de Tchebychev de argumento variable, esto es:
y se obtiene
la forma explícita del determinante que se empleó para graficar los
polinomios de Tchebychev de argumento variable, esto es:
| (4.52) |
Se graficó el espectro de frecuencias para m = 1,2,...,10, usando
el sistema de computación IBM-1130, además debido a la complejidad del
álgebra fue necesario encontrar una relación de recurrencia para los polinomios
de Tchebychev (apéndice E) resultando que el polinomio característico
finalmente está dado por