Ahora queremos una nueva representación para poder calcular el
polinomio característico ![]() , con lo cual podemos
calcular la matriz
, con lo cual podemos
calcular la matriz ![]() para esto es necesario poner los
elementos de la matriz de transferencia en términos de los
parámetros
para esto es necesario poner los
elementos de la matriz de transferencia en términos de los
parámetros ![]() y
y ![]() definidos por (4.1) y (4.2)
respectivamente.
definidos por (4.1) y (4.2)
respectivamente.
Con esta notación resulta:
Por lo tanto la matriz de transferencia resulta de la forma:
![\begin{displaymath}
T =\left[\begin{array}{cccc}
-4Y & 2(4Y+1)(1-2\xi) & -4Y ...
... 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0
\end{array}\right]
\end{displaymath}](img518.gif) |
(4.35) |
Empleando la ecuación (4.7) para el polinomio
característico de ![]() en función de sus raíces resulta
en función de sus raíces resulta
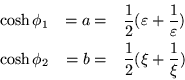
| (4.37) |
Por otra parte anteriormente definimos que ![]() , por
analogía definamos:
, por
analogía definamos:
Usando la ecuación (4.38), junto con las ecuaciones
(4.39) y (4.40) resulta:
En términos de las ecuaciones dadas por (4.41), podemos
evaluar ![]() por lo tanto
por lo tanto ![]() . Además este sistema de
coordenadas lo utilizamos para graficar el espectro de frecuencias
obtenido a partir de la condición de que el menor de la matriz
. Además este sistema de
coordenadas lo utilizamos para graficar el espectro de frecuencias
obtenido a partir de la condición de que el menor de la matriz
![]() es cero, esto es:
es cero, esto es: