| (6.4) |
Que se tiene una asíntota horizontal en ![]() ; un polo en
; un polo en
![]() y un cero
y un cero ![]()
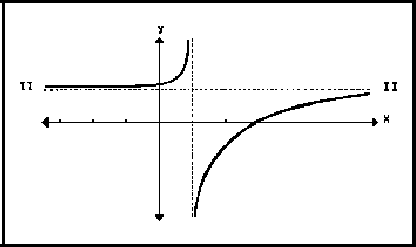
y superponiendo las dos gráficas, ya que pertenecen a la misma
ecuación, resulta
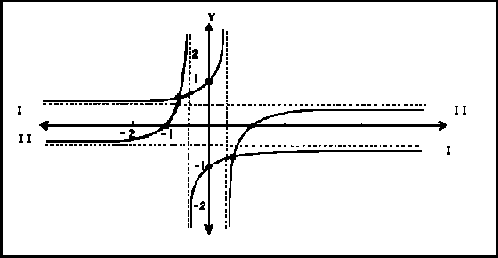
Por lo tanto vemos que existe una verdadera intersección de los dos lugares geométricos; estos puntos de intersección se pueden localizar de la siguiente manera: De (6.3) y (6.4)
efectuando los productos y simplificando resulta que
y sustituyendo el valor de ![]() en cada una de las ecuaciones
(6.3) y (6.4) se encuentra que la intersección
ocurre en los puntos
en cada una de las ecuaciones
(6.3) y (6.4) se encuentra que la intersección
ocurre en los puntos ![]() y
y ![]() .
.
Por un procedimiento similar tenemos para ![]() el polinomio
característico resulta ser
el polinomio
característico resulta ser
y después de cierta álgebra, resulta el polinomio factorizado en la forma siguiente
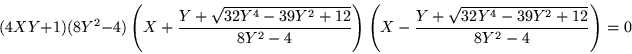
graficando estos factores independientemente y superponiendo las gráficas resulta finalmente que:
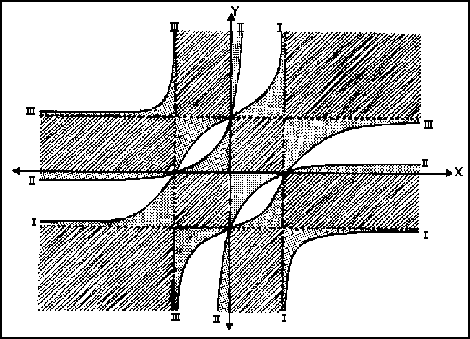
En esta gráfica se muestra claramente la intersección de las
diferentes trayectorias; en esta gráfica tenemos asíntotas
verticales en:
![]() y
y ![]() y
una asíntota horizontal en
y
una asíntota horizontal en ![]() .
.
Por un análisis similar, se puede demostrar para ![]() , y
, y ![]() ,
ya que para argumentos más grandes el álgebra se complica
bastante.
,
ya que para argumentos más grandes el álgebra se complica
bastante.