Degeneración por cruzamiento.

Vamos a ver un ejemplo de que la degeneración que ocurre en la gráfica del espectro de eigenvalores (gráfica VI.I) es por cruzamiento de dos trayectorias; para ello calculemos el polinomio característico (4.53) por ejemplo para $m=1$, usando además la forma explícita de los polinomios de Tchebychev, dados por las ecuaciones (D-7).

Por lo tanto si $m=1$

$$\begin{eqnarray*} x_1(z_1 ,z_2) = & -\frac{1}{4}\sum_{k=0}^2 (3-k)\{ U_k(Z_1)U_k... ...4}\{3U_0(Z_1)U_0(Z_2)+2U_1(Z_1)U_1(Z_2)+U_2(Z_1)U_2(Z_2)\} & = 0 \end{eqnarray*}$$

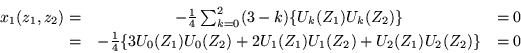
Usando las ecuaciones (D-7) y haciendo $Z_1=X$ y $Z_2=Y$ resulta

$$(4X^2 -1)(4Y^2 -1) +2(2X)(2Y) +3 =0$$

factorizando y agrupando términos resulta finalmente que.

$$4X^2 Y^2 +1= (X-Y)^2$$

Ahora solucionando la ecuación para $Y$ tenemos

$$Y^2 (4X^2 -1) +Y(2X) +(1-X^2) =0$$ (6.1)

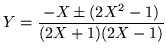$$Y =\frac{-X\pm (2X^2 -1)}{(2X+1)(2X-1)}$$ (6.2)

Por lo tanto en forma factorizada tenemos que (6.1) toma la forma:

$$(4X^2 -1)(Y+\frac{X-(2X^2 -1)}{(2X+1)(2X-1)}) (Y+\frac{X+(2X^2 -1)}{(2X+1)(2X-1)}) = 0$$

o lo que es lo mismo

$$[(2X+1)Y +(X+1)][(2X-1)Y -(X-1)] = 0$$

Por lo tanto tenemos dos factores que debemos analizar, esto es