Modificación de un elemento de la matriz de movimiento.

Lo que se trata de cambiar en este modelo, son las condiciones para la última partícula, la cual equivale a cambiar el elemento de la esquina superior izquierda de la matriz $M$. Esto es, queremos cambiar el elemento $a_0$ físicamente sería necesario cambiar algunos elementos más, pero vamos a analizar que pasa con el cambio de este elemento únicamente.

Anteriormente vimos que para el caso de una cadena sin modificación la relación de recurrencia tenía la forma

$$X_{n+2} =T_d^n X_2$$

Ya que en este caso considerábamos que todas las masas de nuestro modelo eran iguales, pero ahora con las modificaciones del resorte en su extremo resulta:

$$X_{n+2} =(T_d^{\prime} T_d^{-1}) (T_d^n) X_2$$ (9.1)

Ya que vamos a reemplazar la última partícula, lo cual equivale a cambiar $a_0$ por $a_0^{\prime}$ y por lo consiguiente $T$ por $T'$, por lo tanto $T'\, T^{-1}$ es un producto matricial de la forma

$$T_d^{\prime} T_d^{-1} \left[\begin{array}{cccr} \gamma ... ... & 0 & 1 \\ -1 & \gamma & \beta & \gamma \end{array}\right]$$

En donde, como vimos anteriormente (ecs. 2.13), $\beta =\frac{\lambda -a_0}{a_2}$ y por lo tanto $\beta' =\frac{\lambda -a_0^{\prime}}{a_2}$, por lo cual

$$\beta' -\beta =\frac{a_0 -a_0^{\prime}}{a_2} =\epsilon$$ (9.2)

por lo tanto el producto se reduce finalmente a que

$$T_d^{\prime} T_d^{-1} = \left[\begin{array}{cccc} 1 & 0 ... ... 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]$$

Como lo que nos interesa calcular es $(T_d^{\prime}\; T_d^{-1})T_d^n$ y como no conocemos la forma explícita de $M^n$ podemos suponer que es de la forma

$$T_d^{(n)} = \left[\begin{array}{cccc} t_{11} & t_{12} & ... ...} \\ t_{41} & t_{42} & t_{43} & t_{44} \end{array}\right]$$

Por lo tanto el producto matricial $(T_d^{\prime}\; T_d^{-1})T_d^n$ queda finalmente

$$(T_d^{\prime}\; T_d^{-1})T_d^n = \left[\begin{array}{cccc}... ...} \\ t_{41} & t_{42} & t_{43} & t_{44} \end{array}\right]$$

Entonces aplicando la condición que determina los eigenvalores (ec. 2.18) resulta

$$T_{d11}^{(n)} =\left\vert\begin{array}{cc} t_{11} +\epsil... ...silon t_{32} \\ t_{21} & t_{22} \end{array}\right\vert = 0$$

Que se puede factorizar en la forma siguiente:

$$\left\vert\begin{array}{cc} t_{11} & t_{12} \\ t_{21} & t_{... ...t_{21} & t_{22} \\ t_{31} & t_{32} \end{array}\right\vert = 0$$ (9.3)

Esta última ecuación polinominal es la que tenemos que interpretar y solucionar, pero antes de hacerlo analicemos algunas cosas.

Como se puede apreciar en (9.3) el primer determinante es la condición para encontrar los eigenvalores del problema sin perturbar y el segundo determinante nos da la forma de la perturbación, ya que sus elementos fueron determinados por los elementos del producto matricial $T'\, T^{-1}$, además hemos visto que recursivamente cada determinante corresponde a una submatriz de $(T^{\prime}\; T^{-1})T^n$.

$$P_1(\lambda)=\left\vert\begin{array}{cc} t_{11} & t_{12} \\... ...{cc} t_{21} & t_{22} \\ t_{31} & t_{32} \end{array}\right\vert$$

son dos polinomios en $\lambda$, entonces de (9.3) resulta que

$$\frac{P_1(\lambda)}{p_2(\lambda)} =\epsilon$$ (9.4)

Que es una fracción racional, que tiene raíces ceros y polos, en donde los ceros son las raíces de la cadena sin perturbar y los polos son las raíces de la cadena menos una partícula, esto es, de la cadena modificada.

Este resultado es análogo al obtenido en interacciones a primeros vecinos, en donde resulta el cociente de dos polinomios igualados a una constante.

Analizando (9.4) vemos que si $\epsilon =0$ reducimos las raíces de la cadena, a las de la cadena sin modificación cuando $\epsilon \neq 0$ obtenemos otras raíces, por lo tanto la gráfica de la fracción racional (9.3) resulta de la forma siguiente.

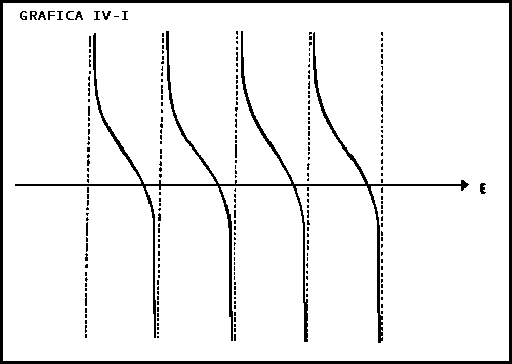
De este tipo de gráficas resultan, cuando comparamos los eigenvalores de una matriz y una submatriz, resultado conocido como teorema de alternación de eigenvalores (ref. [15]), que dice, que el espectro de eigenvalores de una submatriz queda comprendido entre el intervalo de eigenvalores de la matriz original, y además resultan de condiciones para la obtención de las frecuencias en interacciones a primeros vecinos.