Apéndice C

Demostración de que el espectro de eigenvalores para el interior de cualquier cadena y de una cadena con extremos fijos, toma la forma compacta.

$$\left\vert\begin{array}{cl} f(m+2) & -g(m+2) -f(m+1) \\ f(m+1) & -g(m+1) -f(m) \end{array}\right\vert= 0$$

La forma de los elementos de la matriz $t_{11}^{(n)}$, está dada por las ecuaciones (4.32), esto es:

$$\begin{eqnarray*} q_{11} & = & \frac{1}{\,{\mbox{senh}}\phi_1\,{\mbox{senh}}\ph... ... & & -\,{\mbox{senh}}m\phi_2\,{\mbox{senh}}\phi_1\cosh\phi_1\} \end{eqnarray*}$$

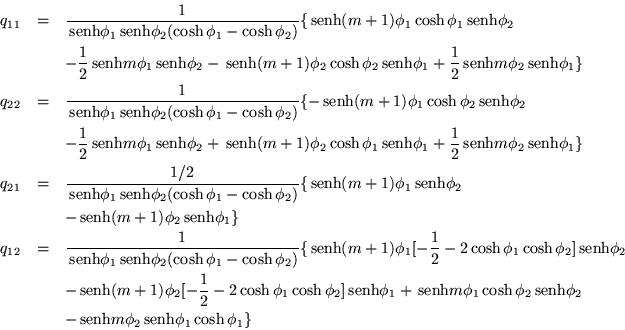
Escribiendo estos términos en forma de determinantes, ignorando por el momento los factores comunes $\,{\mbox{senh}}\phi_1\,{\mbox{senh}}\phi_2(\cosh\phi_1-\cosh\phi_2)$ obtenemos que:

$$q_{11}^{\prime} = \left\vert\begin{array}{cc} \,{\mbox{senh}}(m+1)\phi_1\cosh\phi_1... ...\phi_2 \\ \,{\mbox{senh}}\phi_1 & \,{\mbox{senh}}\phi_2 \end{array}\right\vert$$ (C.1)

$$q_{22}^{\prime} = -\left\vert\begin{array}{cc} \,{\mbox{senh}}(m+1)\phi_1 & \,{\mbo... ...\phi_2 \\ \,{\mbox{senh}}\phi_1 & \,{\mbox{senh}}\phi_2 \end{array}\right\vert$$ (C.2)

$$%% Segundo renglon q_{21}^{\prime} = \frac{1}{2}\left\vert\begin{array}{cc} \,{\mbox{senh}}(m+1)\phi_1... ...\phi_2 \\ \,{\mbox{senh}}\phi_1 & \,{\mbox{senh}}\phi_2 \end{array}\right\vert$$ (C.3)

$$q_{12}^{\prime} = [-\frac{1}{2}-2\cosh\phi_1\cosh\phi_2] \left\vert\begin{array}{cc... ...\phi_2 \\ \,{\mbox{senh}}\phi_1 & \,{\mbox{senh}}\phi_2 \end{array}\right\vert$$

$$+ \left\vert\begin{array}{cc} \,{\mbox{senh}}m\phi_1 & \,{\mbox{s... ...nh}}\phi_1\cosh\phi_1 & \,{\mbox{senh}}\phi_2\cosh\phi_2 \end{array}\right\vert$$ (C.4)

Debido a la forma especial de $T$ se cumple que:

$$q_{ij}^{\prime} (m)=q_{i+1,j}^{\prime} (m-1)$$

En particular

$$\begin{array}{ccc} q_{11}^{\prime} (m) & = & q_{21}^{\pri... ... q_{22}^{\prime} (m-1) & = & q_{12}^{\prime} (m) \end{array}$$ (C.5)

Que para uno $m=m+2$ la ecuaciones (C.5) son

$$\begin{array}{ccc} q_{11}^{\prime} (m+2) & = & q_{21}^{\p... ...q_{22}^{\prime} (m+1) & = & q_{12}^{\prime} (m+2) \end{array}$$ (C.6)

Por ejemplo queremos comprobar la primera relación dada por (C.6), para lo cual es necesario calcular $senh(m+2)\phi_1$

$$\begin{eqnarray*} \,{\mbox{senh}}(m+2)\phi_1 & = & \,{\mbox{senh}}(m+1)\phi_1\c... ...mbox{senh}}m\phi_1\,{\mbox{senh}}\phi_1\} \,{\mbox{senh}}\phi_1 \end{eqnarray*}$$

Efectuando el producto en el último término, y tomando en cuenta que $\,{\mbox{senh}}^2\phi_1 =\cosh^2\phi_1 -1$ resulta

$$\,{\mbox{senh}}(m+2)\phi_1 =\{\,{\mbox{senh}}(m+1)\phi_1\co... ...+\,{\mbox{senh}}m\phi_1\cosh^2\phi_1-\,{\mbox{senh}}m\phi_1\}$$

factorizando términos para introducir $\,{\mbox{senh}}(m+1)\phi_1$ tenemos que

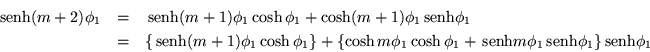
$$\,{\mbox{senh}}(m+2)\phi_1 =2[\,{\mbox{senh}}(m+1)\phi_1\cosh\phi_1 -\frac{1}{2}\,{\mbox{senh}}m\phi_1]$$ (C.7)

Despejando de esta última ecuación el y sustituyéndolo en la ecuación $q_{11}^{\prime}(m+1)$ dado por C.1 resulta

$$\begin{eqnarray*} q_{11}^{\prime} &=& \; \; \; \; \left\vert\begin{array}{cc} ... ...box{senh}}\phi_1 & \,{\mbox{senh}}\phi_2 \end{array}\right\vert \end{eqnarray*}$$

haciendo uso de la propiedad de los determinantes que nos permite separar el primer determinante de $q_{11}^{\prime}$ en dos partes, resulta un determinante exactamente igual, al del segundo término de $q_{11}^{\prime}$ por lo tanto queda finalmente que:

$$q_{11}^{\prime}(m+2)=\frac{1}{2}\left\vert\begin{array}{cc}... ...ox{senh}}\phi_1 & \,{\mbox{senh}}\phi_2 \end{array}\right\vert$$ (C.8)

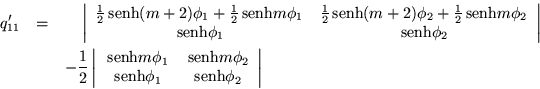
Si comparamos la ecuación (C.8) con (C.3) vemos que son iguales con la única diferencia de que sus argumentos son distintos esto es:

$$q_{21}^{\prime}(m+1) =q_{11}^{\prime}(m+2)$$

Con lo cual queda probada la validez de las ecuaciones (C.6). Además de que el cálculo anterior nos da alguna confianza adicional en el álgebra de la derivación, nos servirá para cálculos posteriores.

Definamos algunas funciones auxiliares:

$$f(k) = \frac{1}{2}\left\vert\begin{array}{cc} \,{\mbox{senh}}k\phi_1 & \... ...\phi_2 \\ \,{\mbox{senh}}\phi_1 & \,{\mbox{senh}}\phi_2 \end{array}\right\vert$$ (C.9)

$$<tex2html_comment_mark>187$$

$$g(k) = \frac{1}{2}\left\vert\begin{array}{cc} \,{\mbox{senh}}k\phi_1 & \... ...hi_2 \\ \,{\mbox{senh}}2\phi_1 & \,{\mbox{senh}}2\phi_2 \end{array}\right\vert$$ (C.10)

Por lo tanto con estas definiciones:

$$\begin{array}{lcl} q_{11}^{\prime} =f(m+2) & &\qquad q_{2... ... =f(m+1) & & \qquad q_{22}^{\prime} =-g(m+1)-f(m) \end{array}$$ (C.11)

En donde las $q$'s difieren de las $q'$'s por el denominador común que es independiente de $k$ y es cero únicamente bajo circunstancias excepcionales.

Por lo tanto, la condición para encontrar el espectro de eigenvalores dado por:

$$\left\vert\begin{array}{cc} q_{11} & q_{12} \\ q_{21} & q_{22} \end{array}\right\vert$$

queda finalmente como:

$$\left\vert\begin{array}{ll} f(m+2) & -g(m+2) -f(m+1) \\ ... ...}\right\vert = 0 \quad \mbox{\hspace{.2in} Q.E.D\hspace{.2in}}$$ (C.12)

o lo que es lo mismo usando la definición de factorización de un determinante que:

$$\left\vert\begin{array}{cc} f(m+2) & g(m+2) \\ f(m+1) & g... ...} f(m+2) & f(m+1) \\ f(m+1) & f(m) \end{array}\right\vert$$