Demostración de que ![]() y
y ![]() definidos por (C.9) y
(C.10) toman la forma en función de los polinomios de
Tchebychev siguiente:
definidos por (C.9) y
(C.10) toman la forma en función de los polinomios de
Tchebychev siguiente:
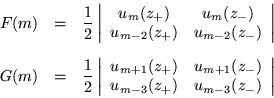
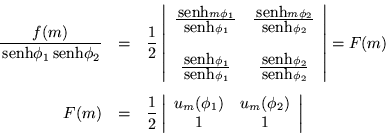
Que es un polinomio de Tchebychev de segunda clase de argumento
imaginario. Para la demostración es necesario el empleo de algunas
identidades trigonométricas, estas son:
usando las ecuaciones (D.1) resulta

Definamos
Procediendo a expresar ![]() en esos mismos términos tenemos.
en esos mismos términos tenemos.
Como vemos (D.3) y (D.4) tienen la forma más simétrica, para los elementos de nuestro determinante.
Las ecuaciones (D.1) nos permiten el cálculo del
denominador opcional, esto es.
Por lo tanto tenemos finalmente que

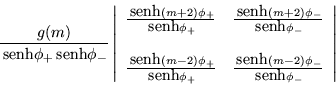
Es posible calcular algunos de los polinomios de subíndices
pequeños, tenemos que
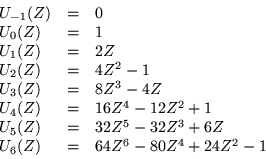 |
(D.7) |
De este modo tenemos, usando (D.5) y (D.6) junto con los polinomios anteriores.
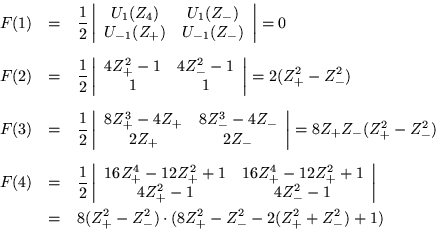
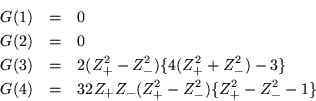

En donde el denominador se obtiene, examinando cuidadosamente la
definición de las ![]() 's, esto es:
's, esto es:

Calculemos
![]()
Por lo tanto
![]()
| (D.10) |
Además como ![]() tiene un rango de
tiene un rango de ![]() a
a ![]() ,
entonces es conveniente examinar a
,
entonces es conveniente examinar a ![]() , en tres regiones
características, esto es:
, en tres regiones
características, esto es:
| Región I | para |
|
|
| Región II | para |
|
|
| Región III | para |
|
En la región I, tenemos la definición estandar de los polinomios de Techebychev.
En la región II, tenemos
En la región III
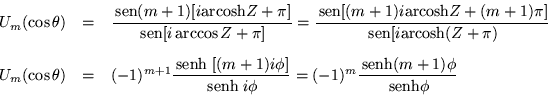
Por lo tanto ![]() restablece la paridad de
restablece la paridad de ![]() en la suma de
polinomios.
en la suma de
polinomios.
Por otra parte, la forma simétrica para ![]() y
y ![]() encontradas anteriormente (ecs. (D.5) y (D.6)), no
nos dan con claridad la forma de variación de los argumentos en los
polinomios de Tchebychev, por lo tanto, es necesario encontrar una
más adecuada, lo cual se logra por uso de
encontradas anteriormente (ecs. (D.5) y (D.6)), no
nos dan con claridad la forma de variación de los argumentos en los
polinomios de Tchebychev, por lo tanto, es necesario encontrar una
más adecuada, lo cual se logra por uso de ![]() y
y ![]() definidos
anteriormente, esto es:
definidos
anteriormente, esto es:
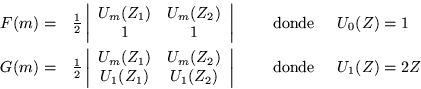
![\begin{eqnarray*}
& & \frac{1}{4\cdot 4(Z_1-Z_2)^2}\\
& &\left\vert \begin{ar...
...+1}(Z_2)]-\frac{1}{2}[U_m(Z_1)-U_m(Z_2)] \end{array}\right\vert
\end{eqnarray*}](img1133.gif)
Usando la relación de recursión
![]() y
agrupando ligeramente, resulta finalmente que:
y
agrupando ligeramente, resulta finalmente que: