- ...Julia 1
- quienes de manera independiente
y casi simultánea obtuvieron resultados equivalentes sobre este
tema de investigación
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... FUNCIONALES2
- SUR LES ÉQUATIONS FONCTIONNELLES (première Mémoire.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ramas1.1
- Markushevich [1] da una amplia definición del concepto.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Tenemos1.2
- en el original:
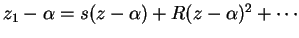
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Obtenemos1.3
- en el original
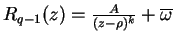
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... capas1.4
- N.T. hojas
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1.5
- en el libro de Markushevich [2] encontramos una amplia explicación
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...itica1.6
- para aclarar este concepto podemos referirnos a George Polya [3], Walter Rudin [4] y Markushevich [2].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
tenemos2.1
- en el original está:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Schr\"oder2.2
- N.T. cuya expresión es:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
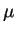 2.3
2.3
- en el original: de radio
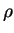
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
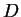 2.4
2.4
- Cf. MONTEL, Sur la représentation conforme (Journ. Math; t. III, 1917, Chap. I,
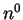 5).
5).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
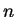 2.5
2.5
- N.T. i.e.
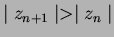
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... positivas2.6
- Estas constantes pueden diferir de aquellas así ya denominadas
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... demostrada2.7
- Deducimos fácilmente de este análisis la igualdad asintótica más precisa
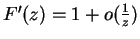 , pero no tendremos necesidad de ella.
, pero no tendremos necesidad de ella.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reentrante2.8
- punto que en repetidas ocasiones es intersectado por la trayectoria de los arcos
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... v\'ertice2.9
- N.T. punto anguloso
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)2.10
- A pesar de la presencia de términos con exponente fraccionario en el desarrollo de
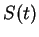 , podemos suponer que
, podemos suponer que 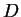 y
y 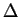 permanecen iguales cualquiera que sea la elección del argumento de
permanecen iguales cualquiera que sea la elección del argumento de
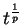 . Los dominios
. Los dominios 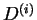 , por ejemplo, son entonces las imagenes de un mismo dominio
, por ejemplo, son entonces las imagenes de un mismo dominio 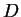 para las transformaciones
para las transformaciones 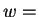
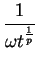
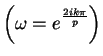 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... imposible2.11
- Frecuentemente daremos, a los puntos dobles o periódicos de multiplicador igual a
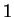 , en módulo, el nombre de puntos dobles o periódicos neutros.
, en módulo, el nombre de puntos dobles o periódicos neutros.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
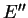 2.12
2.12
- en el original no se da esta notación, sin embargo se utiliza más adelante
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... conforme3.1
- Lo que quiere decir que la dirección determinada por el argumento de
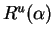 es aquella de la tangente en
es aquella de la tangente en 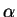 en el círculo.
en el círculo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... divisores3.2
- en el original el índice de la sumatoria en el segundo miembro está expresada como fracción
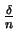
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tenemos3.3
- en el original tenemos
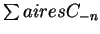 , áreas en plural
, áreas en plural
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 3.4
3.4
- STIELTJES, Recherches sur les fractions continues (Annales de la Faculté
de Toulouse, t. VIII, 1894). - MONTEL, Leçons sur les séries de polynomes à une variable complexe, p. 20 ( Gauthier-Villars, 1910).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... m\'aximo3.5
- en el original no se menciona el término: máximo
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 .
.