Sea ![]() una función racional de grado
una función racional de grado ![]() (
(![]() ) de la variable
compleja
) de la variable
compleja ![]() ; si tenemos
; si tenemos
Uno de los problemas fundamentales que se presentan en el estudio de la iteración
de substituciones racionales es la búsqueda de figuras invariantes
mediante estas substituciones y en primer lugar de los puntos invariantes.
Los puntos invariantes o puntos dobles de substitución: ![]() ,
corresponde a los valores finitos o infinitos de
,
corresponde a los valores finitos o infinitos de ![]() que cumplen la
relación
que cumplen la
relación ![]() . Para que el punto en el infinito sea un punto doble,
es necesario y suficiente que el grado del numerador de
. Para que el punto en el infinito sea un punto doble,
es necesario y suficiente que el grado del numerador de ![]() sea superior al grado
del denominador. Llamamos multiplicador de un punto doble
sea superior al grado
del denominador. Llamamos multiplicador de un punto doble ![]() a un
número
a un
número ![]() igual a
igual a ![]() si
si ![]() es finito, y a
es finito, y a
![]() si
si ![]() es infinito. Verificamos inmediatamente que
ese número
es infinito. Verificamos inmediatamente que
ese número ![]() es relativamente invariante a toda transformación
homográfica efectuada simultaneamente sobre las variable
es relativamente invariante a toda transformación
homográfica efectuada simultaneamente sobre las variable ![]() y
y ![]() y más generalmente a toda transformación conforme regular y biunívoca
en la vecindad de un punto doble. Tenemos1.2 por otra parte, en la vecindad de
y más generalmente a toda transformación conforme regular y biunívoca
en la vecindad de un punto doble. Tenemos1.2 por otra parte, en la vecindad de
![]() ,
,
o, si ![]() está en el infinito,
está en el infinito,
La condición necesaria y suficiente para que el punto doble ![]() sea
raíz múltiple de la ecuación
sea
raíz múltiple de la ecuación ![]() es que el multiplicador
es que el multiplicador ![]() sea igual a
sea igual a ![]() . Si esto se cumple tendremos; en la vecindad de ese
punto doble, supuesta raíz de orden
. Si esto se cumple tendremos; en la vecindad de ese
punto doble, supuesta raíz de orden ![]() de la ecuación
de la ecuación ![]() ,
,
o, si ![]() está en el infinito,
está en el infinito,
El número total de puntos invariantes, cada uno
contado con su grado de multiplicidad como raíz de
![]() , es igual a
, es igual a ![]() .
.
Vamos a establecer una relación importante entre los multiplicadores
de puntos dobles de una misma substitución racional. Podemos suponer que el
punto en el infinito no es un punto doble. Suponemos, además,
que los puntos dobles son todos distintos. Consideremos entonces la fracción
racional:
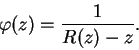
Los puntos dobles ![]() son polos simples de
son polos simples de ![]() la que, por otra
parte, se anula en el infinito. Tenemos entonces
la que, por otra
parte, se anula en el infinito. Tenemos entonces
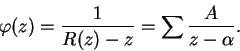
Encontramos inmediatamente
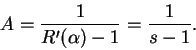
Igualando los términos principales ( en
![]() ) de los dos últimos
miembros, deducimos
) de los dos últimos
miembros, deducimos
ó
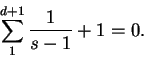
Tal es la relación fundamental que queríamos establecer.
Una consecuencia fácil de ésta relación es la existencia de al menos un punto doble de multiplicador más grande, en módulo, que la unidad.
Pongamos, en efecto,
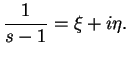 |
Se sigue que
Las relaciones
equivalen respectivamente a
es decir que la circunferencia
![]() , el exterior y el interior de ésta
circunferecia corresponden respectivamente, en el plano de la variable
, el exterior y el interior de ésta
circunferecia corresponden respectivamente, en el plano de la variable ![]() ,
a la recta
,
a la recta
![]() , y a los semiplanos a derecha e izquierda
de ésta recta. En virtud de la relación fundamental, tenemos
, y a los semiplanos a derecha e izquierda
de ésta recta. En virtud de la relación fundamental, tenemos
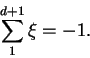
Como ![]() es al menos igual a
es al menos igual a ![]() (
(![]() ), los
), los ![]() no son todos inferiores
o iguales a
no son todos inferiores
o iguales a ![]() , por eso resultaría
, por eso resultaría
![]() .
Tenemos entonces, para al menos un punto doble,
.
Tenemos entonces, para al menos un punto doble,
ó
Remarquemos que podemos dar valores arbitrarios a todos los multiplicadores,
excepto a aquel que se encuentra determinado por la relación fundamental;
es posible entonces, no tener más que un solo punto doble para el cual ![]() sea superior
a la unidad.
sea superior
a la unidad.
Si consideramos los coeficientes de la fracción ![]() de grado
de grado ![]() como
variables independientes, las
como
variables independientes, las ![]() que son funciones algebraicas de esos
coeficientes cumplen igualmente la relación fundamental. Si esos
coeficientes tienden a valores numéricos tales que alguna
que son funciones algebraicas de esos
coeficientes cumplen igualmente la relación fundamental. Si esos
coeficientes tienden a valores numéricos tales que alguna ![]() llegue a ser
igual a
llegue a ser
igual a ![]() y por consecuencia
y por consecuencia
![]() infinito, existe, en virtud de
la relación fundamental, otro multiplicador que tiende a
infinito, existe, en virtud de
la relación fundamental, otro multiplicador que tiende a ![]() .
.
Suponemos ahora que, no siendo el infinito un punto doble, ciertos multiplicadores
sean iguales a ![]() . Tendremos entonces para la fracción
. Tendremos entonces para la fracción
![]() una
descomposición en elementos simples de la forma
una
descomposición en elementos simples de la forma
![\begin{displaymath}
\frac{1}{R(z)-z} = \sum\frac{1}{s-1}\frac{1}{z-\alpha} + \su...
...}}{(z-\beta)^{q-1}} + \cdots + \frac{a_{-1}}{z-\beta} \right],
\end{displaymath}](img67.png)
la segunda sumatoria siendo extendida a los puntos dobles del multiplicador
igual a ![]() y el entero
y el entero ![]() siendo como consecuencia
siendo como consecuencia ![]() . De lo anterior deducimos,
entre los coeficientes
. De lo anterior deducimos,
entre los coeficientes ![]() y los multiplicadores
y los multiplicadores ![]() diferentes de
diferentes de
![]() , la relación
, la relación
Consideramos ahora una función ![]() , la iterada de
, la iterada de ![]() , y las
raíces de la ecuación
, y las
raíces de la ecuación
Sea ![]() cualquier punto y
cualquier punto y ![]() el entero más pequeño tal que
el entero más pequeño tal que
![]() ; los puntos
; los puntos
![]() son todos distintos, pues si tuvieramos
son todos distintos, pues si tuvieramos
![]() ,
, ![]() y
y ![]() siendo más pequeñas que
siendo más pequeñas que ![]() , deduciríamos que
, deduciríamos que
es decir
y como
![]() :
:
Si ![]() , tenemos a
, tenemos a
![]() ; por otra parte
; por otra parte ![]() . Entonces
. Entonces ![]() no sería el
entero más pequeño tal que
no sería el
entero más pequeño tal que
![]() .
.
La serie
![]() es periódica, el periodo comprendiendo
es periódica, el periodo comprendiendo ![]() términos siendo distintos todos sus términos. Diremos que los puntos (
términos siendo distintos todos sus términos. Diremos que los puntos (
![]() ) forman un ciclo de orden
) forman un ciclo de orden ![]() .
Todos los puntos del ciclo son raíces de la ecuación
.
Todos los puntos del ciclo son raíces de la ecuación ![]() .
Considerados como puntos dobles de la substitución
.
Considerados como puntos dobles de la substitución ![]() , todos
tienen el mismo multiplicador. En efecto tenemos, suponiendo que ninguno
de los puntos
, todos
tienen el mismo multiplicador. En efecto tenemos, suponiendo que ninguno
de los puntos ![]() esté en el infinito,
esté en el infinito,
el número ![]() es el multiplicador del ciclo.
es el multiplicador del ciclo.
Subrayemos que las raíces de ![]() se distribuyen en ciclos cuyos
ordenes son divisores de
se distribuyen en ciclos cuyos
ordenes son divisores de ![]() . En particular, entre esas raíces, se
encuentran aquellas de
. En particular, entre esas raíces, se
encuentran aquellas de ![]() , es decir los puntos dobles. Sea
, es decir los puntos dobles. Sea ![]() un punto doble de multiplicador
un punto doble de multiplicador ![]() , de suerte que
, de suerte que
Fácilmente encontramos por recurrencia
ó
Se deduce que en tanto ![]() es diferente de la unidad,
es diferente de la unidad, ![]() es un cero
del mismo orden de multiplicidad para
es un cero
del mismo orden de multiplicidad para ![]() y
y ![]() (es entonces
un cero simple). Es lo mismo si
(es entonces
un cero simple). Es lo mismo si ![]() , pues en cuyo caso tenemos
, pues en cuyo caso tenemos
es decir que ![]() es un cero de orden
es un cero de orden ![]() para éstas dos expresiones.
para éstas dos expresiones.
Ahora suponemos que ![]() es una raíz primitiva de
es una raíz primitiva de ![]() (
(![]() ).
Si
).
Si ![]() no es múltiplo de
no es múltiplo de ![]() ,
, ![]() es una raíz simple de las dos
ecuaciones. Si
es una raíz simple de las dos
ecuaciones. Si ![]() es múltiplo de
es múltiplo de ![]() ,
, ![]() es una raíz simple de la
primera ecuación y raíz de al menos orden
es una raíz simple de la
primera ecuación y raíz de al menos orden ![]() para la segunda:
exactamente de orden
para la segunda:
exactamente de orden ![]() si
si ![]() , es decir si
, es decir si ![]() es múltiplo
de
es múltiplo
de ![]() , de orden superior a
, de orden superior a ![]() , si
, si ![]() no es múltiplo de
no es múltiplo de ![]() .
.
Si ![]() es un número primo absoluto, distinto de los enteros
es un número primo absoluto, distinto de los enteros ![]() en número
límite correspondiendo a los multiplicadores de los puntos dobles que son
de la forma
en número
límite correspondiendo a los multiplicadores de los puntos dobles que son
de la forma
![]() , los ceros de
, los ceros de ![]() son ceros del
mismo orden de multiplicidad que los de
son ceros del
mismo orden de multiplicidad que los de ![]() ; los ceros de ésta última función que no pertenecen a la primera, en total
; los ceros de ésta última función que no pertenecen a la primera, en total ![]() , forman
, forman
![]() ciclos de orden
ciclos de orden ![]() . Veamos entonces que
existen ciclos de puntos de orden tan elevado como queremos, particularmente
ciclos de orden
. Veamos entonces que
existen ciclos de puntos de orden tan elevado como queremos, particularmente
ciclos de orden ![]() cuando
cuando ![]() es un número primo superior a un cierto
límite.
es un número primo superior a un cierto
límite.
Consideremos una fracción racional ![]() tal que
tal que ![]() tenga todas sus raíces distintas; sea
tenga todas sus raíces distintas; sea ![]() un número primo
distinto de los enteros
un número primo
distinto de los enteros ![]() definidos en el parágrafo anterior y
definidos en el parágrafo anterior y ![]() el
multiplicador de un ciclo de orden
el
multiplicador de un ciclo de orden ![]() . Si ningun
. Si ningun ![]() es igual
a
es igual
a ![]() , el análisis del parágrafo 2 aplicado a
, el análisis del parágrafo 2 aplicado a ![]() conduce a la
relación
conduce a la
relación
la primera sumatoria siendo extentida a
![]() ciclos de orden
ciclos de orden
![]() , la segunda a
, la segunda a ![]() puntos dobles de multiplicadores
puntos dobles de multiplicadores ![]() .
.
Para ![]() , tenemos la relación
, tenemos la relación
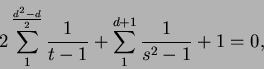
válida en tanto ningun ![]() sea igual a
sea igual a ![]() , ni ningun
, ni ningun ![]() sea igual
a
sea igual
a ![]() . Multiplicamos por
. Multiplicamos por ![]() los dos miembros de ésta relación y le sustraemos la siguiente
los dos miembros de ésta relación y le sustraemos la siguiente
Con lo que obtenemos

Esta relación que tiene lugar igualmente cuando los coeficientes de ![]() son arbitrarios conserva un sentido cuando ciertas
son arbitrarios conserva un sentido cuando ciertas ![]() tienden a
tienden a ![]() y
sigue cumpliendose, como lo expondremos en detalle al final de este parágrafo,
una condición para reemplazar
y
sigue cumpliendose, como lo expondremos en detalle al final de este parágrafo,
una condición para reemplazar ![]() por
por ![]() un número de veces igual
a la suma de los ordenes de multiplicidad de los puntos dobles de multiplicador
un número de veces igual
a la suma de los ordenes de multiplicidad de los puntos dobles de multiplicador
![]() como raíces de la ecuación
como raíces de la ecuación ![]() .
.
Se deriva fácilmente de esta relación (donde suponemos ![]() ,
,
![]() ) que siempre existen ya sea un valor de
) que siempre existen ya sea un valor de ![]() , ó dos valores de
, ó dos valores de ![]() superiores a la unidad en módulo, o bien un
superiores a la unidad en módulo, o bien un ![]() igual a
igual a ![]() y otro más grande en módulo que
y otro más grande en módulo que ![]() . En efecto si tenemos
. En efecto si tenemos
![]() para todos las parejas de orden dos, ningun
para todos las parejas de orden dos, ningun ![]() siendo igual a
siendo igual a ![]() , y un solo
, y un solo ![]() , que designamos por
, que designamos por ![]() , siendo
superior a
, siendo
superior a ![]() , en módulo, igualando a cero
la parte real del primer miembro, la relación precedente da:
, en módulo, igualando a cero
la parte real del primer miembro, la relación precedente da:
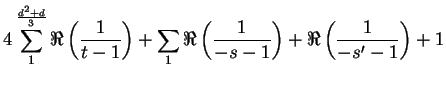 |
|||
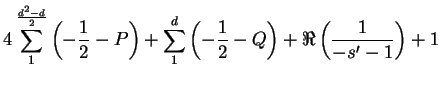 |
siendo ![]() y
y ![]() dos cantidades positivas o nulas. Como
dos cantidades positivas o nulas. Como ![]() ,
,
![]() , de lo que obtenemos:
, de lo que obtenemos:
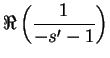 |
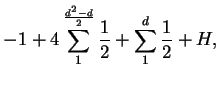 |
||
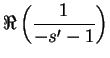 |
siendo H y K dos cantidades positivas o nulas.
Por otra parte, la relación fundamental del parágrafo 2 da
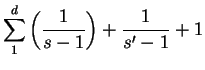 |
|||
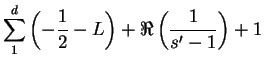 |
|||
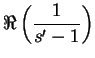 |
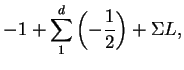 |
||
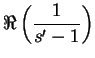 |
Tendremos entonces simultáneamente
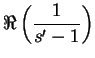 |
|||
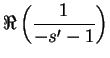 |
Estas dos desigualdades son incompatibles. En efecto, teniendo ![]() , deduciríamos
, deduciríamos
que son evidentes.
Suponemos ahora un ![]() igual a
igual a ![]() (conservando las hipótesis
(conservando las hipótesis ![]() ,
, ![]() ). La igualdad
). La igualdad
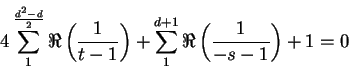
muestra entonces, que existe un ![]() o un
o un ![]() superior a
1 lo que se deriva del análisis del parágrafo 2.
superior a
1 lo que se deriva del análisis del parágrafo 2.
Combinando estos resultados con aquellos de la sección 2, veamos en definitiva
que siempre existe ya sea dos puntos dobles distintos, o un punto doble
y una pareja periódica de orden ![]() cuyos multiplicadores son superiores
a
cuyos multiplicadores son superiores
a ![]() en módulo o iguales a
en módulo o iguales a ![]() .
.
Ahora suponemos que ![]() es un número primo cualquiera distinto de los
enteros
es un número primo cualquiera distinto de los
enteros ![]() considerados anteriormente. Tenemos la relación
considerados anteriormente. Tenemos la relación

si ningún ![]() ni ningún
ni ningún ![]() es igual a
es igual a ![]() . Se sigue, como veremos, que
para
. Se sigue, como veremos, que
para ![]() suficientemente grande, existe al menos un
suficientemente grande, existe al menos un ![]() superior en
módulo a la unidad, pues igualando a cero la parte real del primer miembro,
tenemos
superior en
módulo a la unidad, pues igualando a cero la parte real del primer miembro,
tenemos
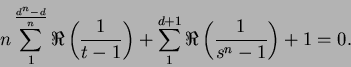
El segundo término del primer miembro queda acotado cualquiera que sea ![]() ; pues la parte
real de
; pues la parte
real de
![]() tiende a
tiende a ![]() para
para ![]() infinito si
infinito si
![]() , a cero si
, a cero si
![]() y es igual a
y es igual a
![]() si
si
![]() , tenemos entonces para cualquiera que sea
, tenemos entonces para cualquiera que sea ![]() ,
,
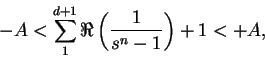
siendo ![]() fija. Si todos los
fija. Si todos los ![]() fueran inferiores a
fueran inferiores a ![]() ,
tendríamos
,
tendríamos
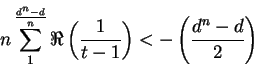
en valor algebraico; y por consiguiente
lo que es claramente imposible,
![]() tiende a infinito junto con
tiende a infinito junto con ![]() . Así que, si una substitución racional no tiene más que puntos invariantes
distintos, posee ciclos de orden
. Así que, si una substitución racional no tiene más que puntos invariantes
distintos, posee ciclos de orden ![]() cuyo multiplicador es más grande que
cuyo multiplicador es más grande que
![]() en módulo o igual a
en módulo o igual a ![]() , en el supuesto que
, en el supuesto que ![]() sea un número primo
suficientemente grande.
sea un número primo
suficientemente grande.
Vamos a mostrar que la conclusión subsiste cuando la substitución tiene
puntos invariantes idénticos, es decir de multiplicador igual a ![]() .
En efecto, si primeramente los coeficientes de
.
En efecto, si primeramente los coeficientes de ![]() son arbitrarios,
tenemos las dos relaciones
son arbitrarios,
tenemos las dos relaciones
 |
|||
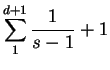 |
de donde deducimos
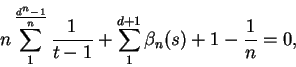
expresando
![]() no tiene polo en
no tiene polo en ![]() ; su valor en ese punto es igual a
; su valor en ese punto es igual a
![]() .
.
La identidad precedente, que tiene lugar cuando los coeficientes de ![]() son arbitrarios, subsiste cuando ciertos multiplicadores
son arbitrarios, subsiste cuando ciertos multiplicadores ![]() llegan a ser iguales a
llegan a ser iguales a ![]() , teneniendo en cuenta que los valores de
, teneniendo en cuenta que los valores de ![]() son múltiplos.
Igualando a cero la parte real del primer miembro, tenemos
son múltiplos.
Igualando a cero la parte real del primer miembro, tenemos
![\begin{displaymath}
\sum^{\frac{d^n - d}{n}}_{1}\Re\left(\frac{1}{t - 1}\right) + \sum^{d + 1}_{1}\Re[\beta_n(s)] + 1 - \frac{1}{n} = 0.
\end{displaymath}](img169.png)
Vemos fácilmente que
![]() tiende a cero
si
tiende a cero
si
![]() ,
a
,
a ![]() si
si
![]() , y a
, y a
![]() si
si
![]() , sin
excluir el valor
, sin
excluir el valor ![]() . El análisis precedente muestra entonces que
aunque
. El análisis precedente muestra entonces que
aunque ![]() sobrepase un cierto límite, existe al menos un valor
sobrepase un cierto límite, existe al menos un valor
![]() , que es la conclusión por defecto solamente si existe un
, que es la conclusión por defecto solamente si existe un ![]() .
Es importante justificar de una manera precisa la sustitución de
.
Es importante justificar de una manera precisa la sustitución de ![]() por
por
![]() en la última fórmula, aunque haya puntos invariantes idénticos.
Sea
en la última fórmula, aunque haya puntos invariantes idénticos.
Sea ![]() una fracción racional tal que la ecuación
una fracción racional tal que la ecuación ![]() admite
la raíz
admite
la raíz ![]() con un orden de multiplicidad igual a
con un orden de multiplicidad igual a ![]() , de suerte
que
, de suerte
que
Reemplazemos ![]() por
por
![]() , siendo
, siendo ![]() un parámetro
arbitrario;
un parámetro
arbitrario; ![]() llega a ser
llega a ser
![]() , función racional
de
, función racional
de ![]() y de
y de ![]() . Las raíces de las ecuaciones
. Las raíces de las ecuaciones
son funciones algebraicas de ![]() que son holomorfas para
que son holomorfas para ![]() si
las expresiones
si
las expresiones
no son nulas para ![]() , es decir si los multiplicadores
, es decir si los multiplicadores ![]() y
y ![]() son diferentes de
son diferentes de ![]() para
para ![]() ; si es así los multiplicadores
de los puntos dobles y los ciclos de orden
; si es así los multiplicadores
de los puntos dobles y los ciclos de orden ![]() , para
, para ![]() cualquiera,
teniendo para las expresiones
cualquiera,
teniendo para las expresiones
son igualmente funciones holomorfas de ![]() , continuas por consecuencia
para
, continuas por consecuencia
para ![]() .
.
Consideremos ahora el punto doble ![]() raíz de orden
raíz de orden ![]() de la
ecuación
de la
ecuación ![]() . Para
. Para ![]() infinitamente pequeño, la ecuación
infinitamente pequeño, la ecuación
![]() es decir
es decir
admite ![]() raíces infinitamente pequeñas, formando un ciclo,
y derivables según las potencias de
raíces infinitamente pequeñas, formando un ciclo,
y derivables según las potencias de
![]() ,
,
Los multiplicadores correspondientes tienen por expresión
Estos ![]() multiplicadores toman el valor de
multiplicadores toman el valor de ![]() y son continuos para
y son continuos para ![]() . Vemos aquí que el paso al límite efectuado en el curso de
este parágrafo es una legítima condición de reemplazar
. Vemos aquí que el paso al límite efectuado en el curso de
este parágrafo es una legítima condición de reemplazar ![]() por
por
![]() en las fórmulas un número de veces igual a
en las fórmulas un número de veces igual a
siendo ![]() los ordenes de multiplicidad de los diversos
puntos dobles de multiplicador
los ordenes de multiplicidad de los diversos
puntos dobles de multiplicador ![]() , en calidad de raíces de
, en calidad de raíces de ![]() .
Entonces esto demuestra en todos los casos que existe una infinidad de
ciclos cuyos multiplicadores son superiores a la unidad en valor absoluto
o iguales a
.
Entonces esto demuestra en todos los casos que existe una infinidad de
ciclos cuyos multiplicadores son superiores a la unidad en valor absoluto
o iguales a ![]() . Demostraremos más tarde un teorema mucho más preciso,
a saber que existe solamente un número finito de ciclos cuyos
multiplicadores son mayores o iguales a la unidad en valor absoluto; pero
éste último resultado no podrá ser obtenido más que por métodos trascendentales, a saber,
por la aplicación de los teoremas recientes referentes a las series de
funciones analíticas. El resultado demostrado aquí, el cual nos servirá
para los desarrollos ulteriores; ha sido obtenido, por el contrario, a través
de un método algebraico elemental mismo que puede ser susceptible de desarrollo posterior.
. Demostraremos más tarde un teorema mucho más preciso,
a saber que existe solamente un número finito de ciclos cuyos
multiplicadores son mayores o iguales a la unidad en valor absoluto; pero
éste último resultado no podrá ser obtenido más que por métodos trascendentales, a saber,
por la aplicación de los teoremas recientes referentes a las series de
funciones analíticas. El resultado demostrado aquí, el cual nos servirá
para los desarrollos ulteriores; ha sido obtenido, por el contrario, a través
de un método algebraico elemental mismo que puede ser susceptible de desarrollo posterior.
Ahora vamos a abordar otra investigación igualmente elemental, a saber aquella de los puntos
que solamente tienen un número finito de antecedentes. Sea ![]() uno de tales puntos y
uno de tales puntos y ![]() la fracción racional considerada. Es claro que
la fracción racional considerada. Es claro que ![]() es un punto
periodico, pues teniendo
es un punto
periodico, pues teniendo ![]() dos antecedentes de rangos diferentes
dos antecedentes de rangos diferentes ![]() y
y ![]() que coinciden, tendremos
que coinciden, tendremos
Como
![]() , tenemos también:
, tenemos también: ![]() , es decir que
, es decir que ![]() es
un punto doble de substitución
es
un punto doble de substitución ![]() , expresando
, expresando
Esta última substitución da lugar a una cadena de antecedentes de ![]() que
designaremos por
que
designaremos por
y cada uno de éstos es antecedente inmediato de aquel que está escrito a su izquierda,
es decir tenemos
de donde deducimos
Siendo finito el número de antecedentes distinto de ![]() , tendremos
, tendremos
de donde
Ahora bien, evidentemente
Por consiguiente,
Entonces todos los antecedentes inmediatos de ![]() son iguales a
son iguales a ![]() . Si
procuramos que, para una transformación homográfica previa,
. Si
procuramos que, para una transformación homográfica previa, ![]() sea
el punto en el infinito, la ecuación
sea
el punto en el infinito, la ecuación ![]() teniendo solamente
raíces infinitas,
teniendo solamente
raíces infinitas, ![]() es un polinomio.
es un polinomio.
Entonces somos llevados a tratar el problema siguiente:
Encontrar las funciones racionales ![]() para la cual una de las iteradas
para la cual una de las iteradas
![]() sea un polinomio.
sea un polinomio.
Si ![]() no es un polinomio, sea
no es un polinomio, sea
![]() un polo de
un polo de ![]() a distancia
finita. En virtud de la identidad
a distancia
finita. En virtud de la identidad
la ecuación
produce
De lo anterior se sigue que la fracción racional
![]() no tiende a
infinito más que para
no tiende a
infinito más que para ![]() en el infinito, ésto es entonces un polinomio
en el infinito, ésto es entonces un polinomio ![]() ,
y tenemos
,
y tenemos
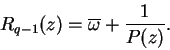
Si R![]() tuviera otro polo
tuviera otro polo
![]() a una distancia finita, tendríamos
a una distancia finita, tendríamos
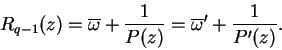
siendo ![]() otro polinomio, esto es imposible, porque deduciríamos
otro polinomio, esto es imposible, porque deduciríamos
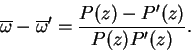
No siendo constantes ![]() y
y ![]() , el grado del numerador en el segundo
miembro es inferior al grado del denominador; la igualdad puede tener lugar
solo si ambos miembros son identicamente nulos;
, el grado del numerador en el segundo
miembro es inferior al grado del denominador; la igualdad puede tener lugar
solo si ambos miembros son identicamente nulos;
![]() .
. ![]() tiene entonces un polo único a distancia finita, y podemos escribirlo
tiene entonces un polo único a distancia finita, y podemos escribirlo
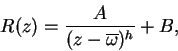
siendo ![]() y
y ![]() dos polinomios en
dos polinomios en ![]() de los cuales el primero es de grado
inferior a
de los cuales el primero es de grado
inferior a ![]() . Vemos que
. Vemos que ![]() es una constante, si no el infinito sería
un punto doble de la sustitución
es una constante, si no el infinito sería
un punto doble de la sustitución ![]() y de todas sus iteradas,
en particular de
y de todas sus iteradas,
en particular de
![]() , que es incompatible con la igualdad
, que es incompatible con la igualdad
![]() que da
que da
![]() .
.
Vamos a ver que ![]() también es una constante. Tenemos, en efecto,
también es una constante. Tenemos, en efecto,
Invirtiendo la regla de las funciones ![]() y
y ![]() en el razonamiento hecho
anteriormente , vemos que
en el razonamiento hecho
anteriormente , vemos que ![]() tiene un polo único
tiene un polo único ![]() a
distancia finita, y además
a
distancia finita, y además
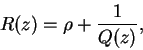
siendo ![]() un polinomio. Igualando las dos expresiones
obtenidas para
un polinomio. Igualando las dos expresiones
obtenidas para ![]() , tenemos
, tenemos
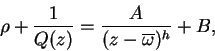
de donde, para ![]()
y como ![]() no es divisible por
no es divisible por
![]() obtenemos enseguida
obtenemos enseguida
Tenemos entonces
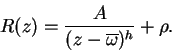
Pero también tenemos para ![]() , que admite el único polo
, que admite el único polo ![]() a distancia finita, la expresión siguiente, donde
a distancia finita, la expresión siguiente, donde ![]() y
y ![]() son polinomios:
son polinomios:
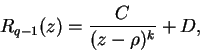
siendo ![]() de grado inferior a
de grado inferior a ![]() y no divisible por
y no divisible por ![]() . Igualando
las dos expresiones de
. Igualando
las dos expresiones de ![]() , tenemos
, tenemos

Haciendo ![]() vemos que
vemos que ![]() es igual a la constante
es igual a la constante
![]() ; de donde se
deduce que
; de donde se
deduce que ![]() es también una constante. Obtenemos1.3 finalmente
es también una constante. Obtenemos1.3 finalmente
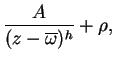 |
|||
 |
siendo ![]() y
y ![]() dos constantes. La identidad
dos constantes. La identidad
da entonces
Deducimos, igualando en los dos miembros los términos en
![]() y
y ![]() (no hay lugar para detenerse en el caso trivial
donde
(no hay lugar para detenerse en el caso trivial
donde ![]() ),
),
Obtenemos finalmente la expresión de ![]() :
:
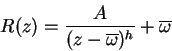
ó

Bajo esta forma, es evidente que las iteradas de orden par de ![]() son
polinomios, mientras que las iteradas de orden impar admiten el polo
son
polinomios, mientras que las iteradas de orden impar admiten el polo
![]() .
.
De lo anterior se sigue fácilmente que dada una substitución racional
![]() , todo punto
, todo punto ![]() admite una infinidad de antecedentes, salvo en los
casos siguientes:
admite una infinidad de antecedentes, salvo en los
casos siguientes: ![]() Si la substitución se lleva a la forma polinomial,
existe un punto: el punto en el infinito, que es igual a todos sus
antecedentes;
Si la substitución se lleva a la forma polinomial,
existe un punto: el punto en el infinito, que es igual a todos sus
antecedentes; ![]() Si la substitución se lleva a la forma
Si la substitución se lleva a la forma ![]() ,
existen dos puntos
,
existen dos puntos ![]() e
e ![]() gozando de ésta misma propiedad;
gozando de ésta misma propiedad;
![]() Si la substitución se lleva a la forma
Si la substitución se lleva a la forma
![]() , hay
dos puntos
, hay
dos puntos ![]() e
e ![]() formando un ciclo de orden dos que constituyen el
conjunto de antecedentes de cada uno de ellos.
formando un ciclo de orden dos que constituyen el
conjunto de antecedentes de cada uno de ellos.
Haremos intervenir frecuentemente, en los capítulos
siguientes, los puntos críticos de las funciones inversas ![]() .
Vamos a mostrar que esos puntos son los consecuentes hasta el rango
.
Vamos a mostrar que esos puntos son los consecuentes hasta el rango ![]() de los puntos críticos de la función
de los puntos críticos de la función ![]() . En efecto,
los puntos críticos
. En efecto,
los puntos críticos ![]() de
de ![]() son los valores de
son los valores de ![]() para
los cuales la ecuación
para
los cuales la ecuación ![]() tiene dos raíces iguales.
De igual forma los puntos críticos de
tiene dos raíces iguales.
De igual forma los puntos críticos de ![]() son los números
son los números
![]() para los cuales la ecuación
para los cuales la ecuación
tiene dos raíces iguales. Esta última ecuación equivale al sistema
| (1.1) |
Que tendrá una raíz doble si alguna de éstas ecuaciones tiene una
raíz doble; y si es la segunda, ![]() es igual a un punto
crítico
es igual a un punto
crítico ![]() de
de ![]() y tenemos
y tenemos
Si la primera ecuación es la que tiene una raíz doble, ![]() es un
punto crítico de la función
es un
punto crítico de la función ![]() . Así se deduce que si la
proposición enunciada es verdadera cuando reemplazamos
. Así se deduce que si la
proposición enunciada es verdadera cuando reemplazamos ![]() por
por ![]() ,
aún es verdadera para
,
aún es verdadera para ![]() , pues los puntos críticos de
, pues los puntos críticos de ![]() son entonces los puntos:
son entonces los puntos:
![]() . Ahora bien,
para
. Ahora bien,
para ![]() , la proposición es una simple tautología; la cual es
entonces general.
, la proposición es una simple tautología; la cual es
entonces general.
Tendremos que completar éstas notas sobre puntos
críticos, pero debemos dar ciertas definiciones y
propiedades simples referentes a los dominios invariantes para una
substitución racional. Sea ![]() un dominio conexo y abierto, es decir un
conjunto de puntos bien conectados y no teniendo más que puntos interiores;
los puntos frontera de
un dominio conexo y abierto, es decir un
conjunto de puntos bien conectados y no teniendo más que puntos interiores;
los puntos frontera de ![]() son los puntos que, no pertenecen a
son los puntos que, no pertenecen a ![]() ,
son límites de puntos de
,
son límites de puntos de ![]() ; si
; si ![]() describe
describe ![]() ,
, ![]() describe
describe ![]() que es también un dominio conexo y abierto (la demostración
es inmediata); los puntos frontera de
que es también un dominio conexo y abierto (la demostración
es inmediata); los puntos frontera de ![]() provienen de puntos frontera de
provienen de puntos frontera de
![]() , lo recíproco
no siempre es verdadero (a menos que se considere
, lo recíproco
no siempre es verdadero (a menos que se considere ![]() extendida sobre
una superficie de Riemann a distintas capas1.4 1.5). Si
extendida sobre
una superficie de Riemann a distintas capas1.4 1.5). Si ![]() y
y ![]() coinciden, diremos que
coinciden, diremos que ![]() es invariante para la substitución
es invariante para la substitución
![]() . Por consecuencia no tendremos que considerar
más que dominios invariantes con frontera invariante, es decir tales que
. Por consecuencia no tendremos que considerar
más que dominios invariantes con frontera invariante, es decir tales que
![]() sea punto frontera
de
sea punto frontera
de ![]() si también lo es de
si también lo es de ![]() . En adelante asumiremos, para
simplificar las discusiones, que se cumple esta condición.
. En adelante asumiremos, para
simplificar las discusiones, que se cumple esta condición.
Ahora vamos a definir la función inversa de ![]() restringida a
restringida a ![]() ;
esto es, para cada punto
;
esto es, para cada punto ![]() en
en ![]() , el conjunto de los valores de la función
, el conjunto de los valores de la función
![]() cuyos puntos representativos son ellos mismos interiores
a
cuyos puntos representativos son ellos mismos interiores
a ![]() , los diversos valores de ésta función, que designamos por
, los diversos valores de ésta función, que designamos por
![]() , se permutan entre sí evolucionando a lo largo de
líneas cerradas interiores a
, se permutan entre sí evolucionando a lo largo de
líneas cerradas interiores a ![]() : pues si
: pues si ![]() y
y ![]() son dos
valores de esta función en el punto
son dos
valores de esta función en el punto ![]() , tenemos
, tenemos
![]() y
y ![]() , siendo interiores a
, siendo interiores a ![]() , pueden estar unidas por una
línea simple
, pueden estar unidas por una
línea simple ![]() interior a
interior a ![]() ;
; ![]() describiendo a
describiendo a ![]() ,
, ![]() describiendo a
describiendo a ![]() igualmente interior a
igualmente interior a ![]() que se cierra en
que se cierra en ![]() : inversamente,
: inversamente, ![]() describiendo el camino cerrado
describiendo el camino cerrado ![]() en
en ![]() , la función
, la función ![]() que
toma en
que
toma en ![]() el valor
el valor ![]() prolongado analíticamente a lo largo de la
línea
prolongado analíticamente a lo largo de la
línea ![]() , tomará el valor
, tomará el valor ![]() en la extremidad de esta línea
recorrida por completo. Recíprocamente si hablamos de
en la extremidad de esta línea
recorrida por completo. Recíprocamente si hablamos de ![]() con la
determinación
con la
determinación ![]() de
de ![]() (siendo
(siendo ![]() interior a
interior a ![]() ), mientras
), mientras ![]() describe caminos interiores a
describe caminos interiores a ![]() , lo mismo sucede con el punto
, lo mismo sucede con el punto
![]() , si no
, si no ![]() alcanzaría la frontera de
alcanzaría la frontera de ![]() y lo mismo sucedería con
y lo mismo sucedería con ![]() , pues suponemos invariante la frontera.
, pues suponemos invariante la frontera.
Deducimos que la función
![]() posee
posee ![]() valores, con
valores, con
![]() independiente de
independiente de ![]() , y éstos valores de
, y éstos valores de ![]() siendo aquellos
que se obtienen a partir de uno de los
valores de la función en un punto de
siendo aquellos
que se obtienen a partir de uno de los
valores de la función en un punto de ![]() por prolongación analítica1.6a lo largo de cualquier camino interior a
por prolongación analítica1.6a lo largo de cualquier camino interior a ![]() . Si ahora consideramos la función
. Si ahora consideramos la función ![]() que deja invariante el dominio
que deja invariante el dominio ![]() y su frontera, la función inversa restringida a
y su frontera, la función inversa restringida a ![]() posee
posee ![]() valores: tenemos, por otra parte, la identidad
valores: tenemos, por otra parte, la identidad
atribuyendo al segundo miembro de las funciones ![]() y
y ![]() sus diversos valores en número
sus diversos valores en número ![]() y
y ![]() respectivamente.
respectivamente.
Los puntos críticos de la función
![]() son los puntos
son los puntos ![]() interiores a
interiores a ![]() tales que la ecuación
tales que la ecuación ![]() tenga al menos dos
raíces idénticas e interiores a
tenga al menos dos
raíces idénticas e interiores a ![]() . La misma observación se hace para
la función
. La misma observación se hace para
la función
![]() . De ésto y del razonamiento hecho al inicio de
éste parágrafo se puede deducir que los puntos
críticos de la función
. De ésto y del razonamiento hecho al inicio de
éste parágrafo se puede deducir que los puntos
críticos de la función
![]() son los consecuentes hasta el rango
son los consecuentes hasta el rango ![]() incluyendo los
puntos críticos de la función
incluyendo los
puntos críticos de la función
![]() .
.
Ahora vamos a introducir una noción igualmente útil para los desarrollos
de los capítulos siguientes, el de dominio completamente invariante;
llamaremos también un dominio que no solamente es invariante por la
substitución considerada, sino que aún contiene todos los
antecedentes de cada uno de sus puntos. Un dominio completamente invariante
tiene siempre una frontera invariante. Vamos a establecer que, si un dominio
completamente invariante es simplemente conexo, siempre encierra al menos ![]() puntos críticos de la función
puntos críticos de la función ![]() . Dejando de lado los casos
fáciles donde
. Dejando de lado los casos
fáciles donde ![]() contiene todo el plano o bien posee un punto frontera
único. Podemos suponer que
contiene todo el plano o bien posee un punto frontera
único. Podemos suponer que ![]() no contienen el punto en el infinito:
concluyendo que
no contienen el punto en el infinito:
concluyendo que ![]() no tiene polos interiores a
no tiene polos interiores a ![]() . Si
. Si ![]() es un punto
interior a
es un punto
interior a ![]() podemos trazar en
podemos trazar en ![]() un contorno cerrado simple
un contorno cerrado simple ![]() (constituido si queremos por un
arco regular y sin punto doble de curva analítica) comprendiendo a
(constituido si queremos por un
arco regular y sin punto doble de curva analítica) comprendiendo a ![]() en
su interior y cuyos puntos están tan próximos a la frontera de
en
su interior y cuyos puntos están tan próximos a la frontera de ![]() como queremos, para convencernos, podemos utilizar
la representación conforme de
como queremos, para convencernos, podemos utilizar
la representación conforme de ![]() sobre un círculo de radio
sobre un círculo de radio ![]() tomando para
tomando para ![]() la curva que corresponde en
la curva que corresponde en ![]() a una circunferencia
de radio
a una circunferencia
de radio ![]() concéntrica al círculo representativo; o aún
hacer un razonamiento directo viendo a
concéntrica al círculo representativo; o aún
hacer un razonamiento directo viendo a ![]() como límite de dominios
acotados por arcos de círculo. Sentado esto, decimos que si
como límite de dominios
acotados por arcos de círculo. Sentado esto, decimos que si ![]() es
suficientemente cercano a la frontera, todas las ramas de la función
es
suficientemente cercano a la frontera, todas las ramas de la función
![]() se permutan circularmente sobre
se permutan circularmente sobre ![]() . En el caso general,
las diversas ramas de una función algebraica, cuando el punto representativo
de la variable describe un contorno cerrado, forman un cierto número de ciclos
distintos y los valores que corresponden a un mismo ciclo se permutan
circularmente entre sí cuando la variable regresa a su punto de
partida. Sea un ciclo de orden
. En el caso general,
las diversas ramas de una función algebraica, cuando el punto representativo
de la variable describe un contorno cerrado, forman un cierto número de ciclos
distintos y los valores que corresponden a un mismo ciclo se permutan
circularmente entre sí cuando la variable regresa a su punto de
partida. Sea un ciclo de orden ![]() de los valores de
de los valores de ![]() sobre
sobre
![]() al cual le co-rres-pon-de una curva
al cual le co-rres-pon-de una curva ![]() descrita por el
punto representativo de
descrita por el
punto representativo de ![]() y que se cierra cuando
y que se cierra cuando ![]() ha descrito
ha descrito
![]() veces
veces ![]() en el mismo sentido; resulta del caracter
completamente invariante de la frontera y de la continuidad de funciones
algebraicas que las curvas
en el mismo sentido; resulta del caracter
completamente invariante de la frontera y de la continuidad de funciones
algebraicas que las curvas ![]() tienden uniformemente a la frontera
al mismo tiempo que
tienden uniformemente a la frontera
al mismo tiempo que ![]() . Ahora consideremos las diversas raíces
. Ahora consideremos las diversas raíces
![]() de la ecuación
de la ecuación ![]() ; que son interiores a
; que son interiores a ![]() y que
pueden estar unidas de dos en dos por las líneas
y que
pueden estar unidas de dos en dos por las líneas ![]() interiores a
interiores a ![]() cuya distancia a la frontera es superior al número positivo
cuya distancia a la frontera es superior al número positivo ![]() ;
como podemos suponer que todos los puntos del contorno cerrado
;
como podemos suponer que todos los puntos del contorno cerrado
![]() están a una distancia de la frontera
menor que
están a una distancia de la frontera
menor que ![]() ,
,
![]() no encuentra las líneas
no encuentra las líneas ![]() ; los puntos
; los puntos ![]() son pues todos interiores ó todos exteriores a
son pues todos interiores ó todos exteriores a ![]() ;
o cuando
;
o cuando ![]() describe una vez
describe una vez ![]() ,
, ![]() describe
describe ![]() veces seguidas en el mismo sentido el contorno cerrado
veces seguidas en el mismo sentido el contorno cerrado ![]() que
encierra a
que
encierra a ![]() en su interior; entonces el argumento de
en su interior; entonces el argumento de ![]() a variado de
a variado de
![]() y, puesto que
y, puesto que ![]() no tiene polos en
no tiene polos en ![]() ; concluimos que
el número de ceros de esta función en el interior de
; concluimos que
el número de ceros de esta función en el interior de ![]() es
igual a
es
igual a ![]() ; como tenemos
; como tenemos ![]() , entonces hacemos que todos los
puntos
, entonces hacemos que todos los
puntos ![]() sean interiores al contorno
sean interiores al contorno ![]() ; pues
; pues ![]() y todas las ramas de la función
y todas las ramas de la función ![]() se permutan circularmente entre
sí a lo largo de
se permutan circularmente entre
sí a lo largo de ![]() .
.
Ahora suponemos que ![]() no tuviera más que los puntos críticos simples
alrededor de los cuales se permutan solamente dos soluciones de esta función,
que es el caso general. Llamemos
no tuviera más que los puntos críticos simples
alrededor de los cuales se permutan solamente dos soluciones de esta función,
que es el caso general. Llamemos ![]() al dominio limitado por
al dominio limitado por
![]() e interior a
e interior a ![]() , puesto que
, puesto que ![]() es simplemente conexo; a partir
de cada uno de los puntos críticos de
es simplemente conexo; a partir
de cada uno de los puntos críticos de ![]() contenido en
contenido en ![]() ,
tracemos un corte extendiendose hasta el contorno
,
tracemos un corte extendiendose hasta el contorno ![]() ;
cuando cruzamos un corte, dos ramas
;
cuando cruzamos un corte, dos ramas ![]() y
y ![]() de la función son
permutadas entre si; decimos que el corte tiene el caracter (
de la función son
permutadas entre si; decimos que el corte tiene el caracter (![]() ).
Sean
).
Sean ![]() los diversos cortes escritos en el orden donde se
suceden sus puntos de intersección con
los diversos cortes escritos en el orden donde se
suceden sus puntos de intersección con ![]() descrito en sentido
directo. Sea
descrito en sentido
directo. Sea
![]() la tabla de
caracteres de éstos cortes. Podemos cambiar el trazo de los cortes de tal
manera que se reestablezca la tabla
la tabla de
caracteres de éstos cortes. Podemos cambiar el trazo de los cortes de tal
manera que se reestablezca la tabla ![]() a la forma canónica
a la forma canónica
Si los puntos críticos de ![]() no son simples, la conclusión
subsiste, un punto crítico al cual le corresponden diferentes ciclos de raíces
de ordenes
no son simples, la conclusión
subsiste, un punto crítico al cual le corresponden diferentes ciclos de raíces
de ordenes
![]() respectivamente
siendo vistos como la reunión de
respectivamente
siendo vistos como la reunión de
![]() puntos críticos simples. Bastará, para convencerse, hacer variar
infinitamente poco los coeficientes de
puntos críticos simples. Bastará, para convencerse, hacer variar
infinitamente poco los coeficientes de ![]() , lo que hará variar
infinitamente poco la posición de los puntos críticos sin modificar
la propiedad que tienen las ramas de
, lo que hará variar
infinitamente poco la posición de los puntos críticos sin modificar
la propiedad que tienen las ramas de ![]() de ser todas permutadas
entre sí sobre
de ser todas permutadas
entre sí sobre ![]() .
.
![]() es el número total de puntos críticos de
es el número total de puntos críticos de ![]() ,
resulta de lo anterior que no pueden existir más de dos dominios
simplemente conexos y completamente invariantes para substitución
,
resulta de lo anterior que no pueden existir más de dos dominios
simplemente conexos y completamente invariantes para substitución
![]() , si dejamos de lado los dominios que no tienen
más de un punto frontera. Ese resultado es fundamental más tarde.
Ahora consideremos el caso donde el dominio
, si dejamos de lado los dominios que no tienen
más de un punto frontera. Ese resultado es fundamental más tarde.
Ahora consideremos el caso donde el dominio ![]() es invariante para una
cierta potencia de la substitución dada, de suerte que denotando como
es invariante para una
cierta potencia de la substitución dada, de suerte que denotando como
![]() a sus consecuentes sucesivos tendríamos
a sus consecuentes sucesivos tendríamos
![]() ; el conjunto de dominios
; el conjunto de dominios
![]() forman
entonces un ciclo de dominios invariantes; siempre suponemos que las
fronteras de esos dominios tienen el mismo caracter de invarianza que los
dominios mismos. Cuando
forman
entonces un ciclo de dominios invariantes; siempre suponemos que las
fronteras de esos dominios tienen el mismo caracter de invarianza que los
dominios mismos. Cuando ![]() es interior a uno de ellos,
es interior a uno de ellos, ![]() por ejemplo,
existen ramas de
por ejemplo,
existen ramas de ![]() cuyos puntos representativos son interiores
a
cuyos puntos representativos son interiores
a ![]() ; esas diversas ramas, cuyo número es independiente de la posición de
; esas diversas ramas, cuyo número es independiente de la posición de ![]() en
en ![]() , son aquellas que se deducen de una de ellas
por prolongación analítica a lo largo de los caminos interiores a
, son aquellas que se deducen de una de ellas
por prolongación analítica a lo largo de los caminos interiores a ![]() ;
definimos también la función
;
definimos también la función ![]() restringida a
restringida a ![]() y
pasamos fácilmente de ahí a la definición de la función
y
pasamos fácilmente de ahí a la definición de la función ![]() restringida al dominio
restringida al dominio ![]() , siendo
, siendo ![]() el residuo de
el residuo de ![]() ; los
puntos críticos de ésta última función en
; los
puntos críticos de ésta última función en ![]() son los consecuentes
hasta el rango
son los consecuentes
hasta el rango ![]() de los puntos críticos de las funciones restringidas
de los puntos críticos de las funciones restringidas
![]() correspondiendo a los diversos dominios
correspondiendo a los diversos dominios ![]() . Tomamos por ejemplo
. Tomamos por ejemplo
![]() . Los puntos críticos interiores a
. Los puntos críticos interiores a ![]() de la función
restringida
de la función
restringida ![]() son los puntos
son los puntos
![]() llamando
llamando
![]() a los puntos críticos de las funciones
restringidas
a los puntos críticos de las funciones
restringidas ![]() cuando
cuando ![]() varía sucesivamente en los
dominios
varía sucesivamente en los
dominios ![]() que forman un ciclo de orden
que forman un ciclo de orden ![]() . La nocion de
dominio completamente invariante se extiende partiendo de si misma
a un ciclo de
dominios. Por lo anterior es claro que si un ciclo de dominios de
orden
. La nocion de
dominio completamente invariante se extiende partiendo de si misma
a un ciclo de
dominios. Por lo anterior es claro que si un ciclo de dominios de
orden ![]() es completamente invariante y formado por dominios simplemente
conexos,
es completamente invariante y formado por dominios simplemente
conexos, ![]() no puede más que tener los valores
no puede más que tener los valores ![]() ó
ó ![]() ; pues los dominios
simplemente conexos
; pues los dominios
simplemente conexos
![]() son completamente invariantes
para la subsitución
son completamente invariantes
para la subsitución
![]() luego entonces su número no puede
sobrepasar a dos.
Las nociones de dominio invariante o completamente invariante se extienden
sin dificultad a conjuntos cualquiera. Veremos sin esfuerzo que un conjunto
invariante que no comprende más que un número finito de puntos está formado por
la unión de un número finito de ciclos. Un conjunto completamente
invariante y que no comprende más que un número finito de puntos está formado de
uno o de dos puntos excepcionales (n
luego entonces su número no puede
sobrepasar a dos.
Las nociones de dominio invariante o completamente invariante se extienden
sin dificultad a conjuntos cualquiera. Veremos sin esfuerzo que un conjunto
invariante que no comprende más que un número finito de puntos está formado por
la unión de un número finito de ciclos. Un conjunto completamente
invariante y que no comprende más que un número finito de puntos está formado de
uno o de dos puntos excepcionales (n![]() ).
).