En este capítulo estudiaremos una clase particularmente simple e importante de substituciones racionales, aquellas que transforman en sí mismas respectivamente el interior y la circunferencia de un círculo y por consecuencia también el exterior del círculo. Vamos a buscar la expresión general de tal substitución suponiendo primero que para una inversión previa hubieramos transformado el círculo en el semi-plano: ![]() .
. ![]() es una substitución buscada, la función
es una substitución buscada, la función ![]() que es evidentemente real para
que es evidentemente real para ![]() real tiene todos sus polos sobre el eje real; pues si tuviera un polo
real tiene todos sus polos sobre el eje real; pues si tuviera un polo ![]() en el semi-plano superior, con
en el semi-plano superior, con ![]() describiendo alrededor de
describiendo alrededor de ![]() una circunferencia infinitamente pequeña,
una circunferencia infinitamente pequeña, ![]() describiría un contorno exterior a un círculo de radio infinitamente grande, de manera que habiendo aumentado el argumento de
describiría un contorno exterior a un círculo de radio infinitamente grande, de manera que habiendo aumentado el argumento de ![]() en
en ![]() , el de
, el de ![]() hubiera disminuido en
hubiera disminuido en
![]() y el lugar de
y el lugar de ![]() tendría puntos en el semi-plano inferior, lo cual es imposible, ya que
tendría puntos en el semi-plano inferior, lo cual es imposible, ya que ![]() permanece en el semi-plano superior. Además, los polos de
permanece en el semi-plano superior. Además, los polos de ![]() no pueden ser sino polos simples, pues si
no pueden ser sino polos simples, pues si ![]() describe alrededor del polo real
describe alrededor del polo real ![]() una semi-circunferencia de radio muy pequeño en el semi-plano superior de suerte que el argumento de
una semi-circunferencia de radio muy pequeño en el semi-plano superior de suerte que el argumento de ![]() cruze de
cruze de ![]() a
a ![]() , Z describirá una curva exterior a un círculo de radio muy grande de manera que el argumento de
, Z describirá una curva exterior a un círculo de radio muy grande de manera que el argumento de ![]() disminuye aproximadamente en
disminuye aproximadamente en ![]() , si
, si ![]() es un polo de orden
es un polo de orden ![]() . Si
. Si ![]() , esta curva tendrá puntos en el semi-plano inferior, lo cual es imposible. Veamos de una manera análoga que el infinito es un polo simple de
, esta curva tendrá puntos en el semi-plano inferior, lo cual es imposible. Veamos de una manera análoga que el infinito es un polo simple de ![]() . Tenemos entonces
. Tenemos entonces
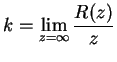 |
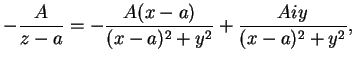 |
Recíprocamente, toda fracción racional de la forma anterior responde a la cuestión, ya que estableciendo ![]() , se obtiene
, se obtiene
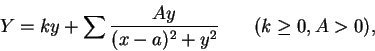
Vamos a buscar los puntos dobles de la substitucion estableciendo ![]() lo que debe ser visto como el caso general; de otro modo, siendo el infinito un punto doble, estableceremos
lo que debe ser visto como el caso general; de otro modo, siendo el infinito un punto doble, estableceremos
Estableceremos entonces
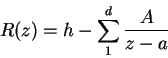
Haremos variar ![]() de
de ![]() a
a ![]() señalando los valores de discontinuidad
señalando los valores de discontinuidad ![]() de
de ![]() ; tenemos la tabla de variación siguiente:
; tenemos la tabla de variación siguiente:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Según la cual hay un número impar de raíces reales, al menos una, en cada uno de los intervalos
![]() , lo que da al menos
, lo que da al menos ![]() raíces reales y distintas, y un número par que no puede ser entonces más que
raíces reales y distintas, y un número par que no puede ser entonces más que ![]() ó
ó ![]() en los intervalos extremos (el número total de raíces, distintas ó no, es
en los intervalos extremos (el número total de raíces, distintas ó no, es ![]() , incluyendo las raíces imaginarias).
, incluyendo las raíces imaginarias).
La ecuación tiene así ![]() raíces reales y distintas respectivamente en los intervalos
raíces reales y distintas respectivamente en los intervalos
![]() , y además siguiendo los casos:
, y además siguiendo los casos:
![]() Dos raíces imaginarias conjugadas.
Dos raíces imaginarias conjugadas.
Hay entonces una raíz simple real y única en cada uno de los intervalos
![]() . Para cada una de estas raíces
. Para cada una de estas raíces ![]() pasa de negativa a positiva, entonces
pasa de negativa a positiva, entonces
![]() ó
ó ![]() . Las
. Las ![]() son entonces puntos dobles repulsores. Consideremos enseguida las dos raíces imaginarias conjugadas, entonces los multiplicadores
son entonces puntos dobles repulsores. Consideremos enseguida las dos raíces imaginarias conjugadas, entonces los multiplicadores ![]() y
y ![]() son igualmente imaginarios conjugados. Según la relación conocida entre los multiplicadores, tenemos
son igualmente imaginarios conjugados. Según la relación conocida entre los multiplicadores, tenemos
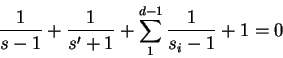
Tenemos dos puntos dobles atractores imaginarios conjugados.
![]() Dos raíces reales distintas entre ellas y de las anteriores, entonces en total
Dos raíces reales distintas entre ellas y de las anteriores, entonces en total ![]() raíces reales y distintas.
raíces reales y distintas.
Entonces necesariamente hay o tres raíces reales y distintas en un intervalo
![]() , o dos raíces reales y distintas en uno de los intervalos extremos. Si hay tres raíces
, o dos raíces reales y distintas en uno de los intervalos extremos. Si hay tres raíces
![]() entre
entre ![]() y
y ![]() , para
, para ![]() y
y ![]() ,
, ![]() es creciente
es creciente
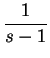
Hay entonces un punto doble atractor y sólo uno sobre el eje real.
![]() Dos raíces reales iguales entre sí o a una de las anteriores, es decir
Dos raíces reales iguales entre sí o a una de las anteriores, es decir ![]() raíces reales y distintas y una raíz doble.
raíces reales y distintas y una raíz doble.
Para la raíz doble, tenemos
![]() . Vemos fácilmente que
. Vemos fácilmente que ![]() para las otras.
para las otras.
![]() Dos raíces reales iguales entre sí y a una de las anteriores, es decir, en total una raíz triple perteneciendo entonces a uno de los intervalos
Dos raíces reales iguales entre sí y a una de las anteriores, es decir, en total una raíz triple perteneciendo entonces a uno de los intervalos
![]() y
y ![]() raíces reales distintas perteneciendo respectivamente a los
raíces reales distintas perteneciendo respectivamente a los ![]() intervalos restantes. Para la primera, tenemos
intervalos restantes. Para la primera, tenemos
![]() ,
,
![]() . Para las restantes tenemos siempre
. Para las restantes tenemos siempre ![]() .
.
Resumamos estas conclusiones considerando un círculo cualquiera en lugar de la parte superior del semi-plano. Podemos decir que toda substitución racional de grado ![]() admitiendo un círculo fundamental
admitiendo un círculo fundamental ![]() poseé:
poseé:
Ya sea ![]() dos puntos dobles atractores que son imagen uno del otro con respecto a
dos puntos dobles atractores que son imagen uno del otro con respecto a ![]() y
y ![]() puntos dobles repulsores situados sobre la circunferencia;
puntos dobles repulsores situados sobre la circunferencia;
Ya sea ![]() un punto doble atractor y
un punto doble atractor y ![]() puntos dobles repulsores, todos situados sobre la circunferencia;
puntos dobles repulsores, todos situados sobre la circunferencia;
Ya sea ![]() un punto doble de multiplicador igual a
un punto doble de multiplicador igual a ![]() que equivale a dos o a tres puntos dobles iguales y
que equivale a dos o a tres puntos dobles iguales y ![]() ó
ó ![]() puntos dobles repulsores, todos sobre la circunferencia.
puntos dobles repulsores, todos sobre la circunferencia.
Señalemos que el multiplicador de un punto doble situado sobre la circunferencia es siempre real y positivo, lo que es poco más o menos a priori. Al contrario de los multiplicadores de los puntos dobles atractores no situados sobre la circunferencia, si existen, pueden tener cualquier valor real o complejo ( con
modulo menor que uno).
Podemos entender la noción de substitución en el círculo fundamental considerando también el caso donde ![]() permutan entre si el interior y el exterior del círculo, la circunferencia permanece invariante. Si transformamos la circunferencia en el eje real, tenemos como consecuencia la expresión de
permutan entre si el interior y el exterior del círculo, la circunferencia permanece invariante. Si transformamos la circunferencia en el eje real, tenemos como consecuencia la expresión de ![]() señalando que
señalando que ![]() deja invariante el semi-plano superior:
deja invariante el semi-plano superior:
Según lo anterior, si ![]() es de la primera especie, es decir poseé dos puntos dobles imaginarios, estos puntos forman un ciclo de orden
es de la primera especie, es decir poseé dos puntos dobles imaginarios, estos puntos forman un ciclo de orden ![]() para
para ![]() . Siendo, además, el resto de los puntos dobles de
. Siendo, además, el resto de los puntos dobles de ![]() todos reales y repulsores, igual que para
todos reales y repulsores, igual que para ![]() . La substitución propuesta tiene entonces todos sus puntos invariantes sobre el eje real con multiplicadores reales y negativos; tiene además un ciclo atractor de orden
. La substitución propuesta tiene entonces todos sus puntos invariantes sobre el eje real con multiplicadores reales y negativos; tiene además un ciclo atractor de orden ![]() .
.
Si ![]() es de la segunda especie, es decir poseé un punto invariante atractor sobre el eje real, siendo los restantes repulsores e igualmente reales.
es de la segunda especie, es decir poseé un punto invariante atractor sobre el eje real, siendo los restantes repulsores e igualmente reales. ![]() tiene igualmente un punto invariante atractor de multiplicador comprendido entre
tiene igualmente un punto invariante atractor de multiplicador comprendido entre ![]() y
y ![]() (límites excluidos) y
(límites excluidos) y ![]() puntos invariantes repulsores, siendo todos estos puntos reales.
puntos invariantes repulsores, siendo todos estos puntos reales.
Si ![]() es de la especie singular, es decir poseé un punto doble de multiplicador igual a
es de la especie singular, es decir poseé un punto doble de multiplicador igual a ![]() ,
, ![]() tendrá sobre el eje real un punto doble de multiplicador igual a
tendrá sobre el eje real un punto doble de multiplicador igual a ![]() [para el cual
[para el cual
![]() ]. El resto de los puntos dobles son reales y repulsores.
]. El resto de los puntos dobles son reales y repulsores.
Hay correspondencia entre las diversas especies para los dos tipos de substitución, excepto a la que concierne las substituciones singulares del primer tipo con un punto doble ![]() donde
donde ![]() ,
,
![]() que no tiene correspondientes en el segundo tipo.
que no tiene correspondientes en el segundo tipo.
Si ![]() es una función en el círculo fundamental, lo será
es una función en el círculo fundamental, lo será ![]() cualquiera que sea el entero
cualquiera que sea el entero ![]() ;
; ![]() será del segundo tipo si
será del segundo tipo si ![]() cumple lo anterior y si
cumple lo anterior y si ![]() es impar.
es impar.
Se obtiene por consecuencia que todos los ciclos de orden ![]() son repulsores y están formados de los puntos reales mientras
son repulsores y están formados de los puntos reales mientras ![]() o bien
o bien ![]() , a excepción de las substituciones del segundo tipo de la primera especie.
, a excepción de las substituciones del segundo tipo de la primera especie.
De una manera general, formando entre ellas substituciones que admiten el mismo círculo fundamental ![]() , en un orden cualquiera, tenemos aún una substitución que admite el mismo círculo fundamental; estas substituciones forman un grupo si les agregamos sus inversas que, naturalmente, no son racionales.
, en un orden cualquiera, tenemos aún una substitución que admite el mismo círculo fundamental; estas substituciones forman un grupo si les agregamos sus inversas que, naturalmente, no son racionales.
Las propiedades de los puntos dobles que acabamos de estudiar caracterizan las substituciones en el círculo fundamental y permiten expresarlas de alguna otra manera.
Supongamos que ![]() admite
admite ![]() puntos dobles
puntos dobles
![]() situados sobre una circunferencia
situados sobre una circunferencia ![]() , de multiplicadores reales y mayores que
, de multiplicadores reales y mayores que ![]() , y dos puntos dobles
, y dos puntos dobles
![]() de multiplicadores
de multiplicadores ![]() y
y ![]() conjugados, siendo
conjugados, siendo ![]() y
y ![]() imagen uno del otro con respecto a
imagen uno del otro con respecto a ![]() ; los
; los ![]() están ligados por la relación
están ligados por la relación
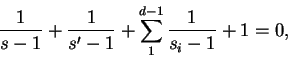
Decimos que la substitución admite a ![]() como círculo fundamental. Sabemos en efecto que
como círculo fundamental. Sabemos en efecto que
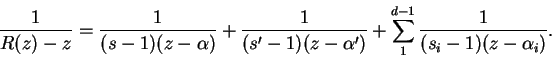
Podemos suponer, sin restar generalidad, que ![]() es el eje real, entonces
es el eje real, entonces ![]() real,
real, ![]() y
y ![]() imaginarios conjugados. Establecemos
imaginarios conjugados. Establecemos ![]() en la igualdad anterior; tenemos una ecuación en
en la igualdad anterior; tenemos una ecuación en ![]() que tendrá todas sus raíces reales si
que tendrá todas sus raíces reales si ![]() es real. En efecto, esta ecuación puede escribirse
es real. En efecto, esta ecuación puede escribirse
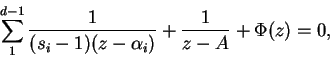
con ![]() real y acotada para
real y acotada para ![]() real, pues es una fracción racional de la forma
real, pues es una fracción racional de la forma
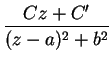 , donde
, donde ![]() . Por otra parte, los coeficientes
. Por otra parte, los coeficientes
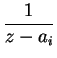 son positivos ya que
son positivos ya que ![]() , al igual que el coeficiente de
, al igual que el coeficiente de
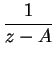 que es igual a
que es igual a ![]() . Entonces, si consideramos los
. Entonces, si consideramos los ![]() intervalos
determinados por los
intervalos
determinados por los ![]() números
números
![]() ; cuando el primer miembro toma valores infinitos de signos contrarios a los dos extremos de un intervalo se anula una vez en este intervalo; así pues tenemos
; cuando el primer miembro toma valores infinitos de signos contrarios a los dos extremos de un intervalo se anula una vez en este intervalo; así pues tenemos ![]() raíces reales, y como la ecuación es de grado
raíces reales, y como la ecuación es de grado ![]() (a causa de la relación entre los multiplicadores), hay
(a causa de la relación entre los multiplicadores), hay ![]() raíces reales. Entonces
raíces reales. Entonces ![]() tiene todas sus raíces reales para
tiene todas sus raíces reales para ![]() real; pero coincidiendo
real; pero coincidiendo ![]() con
con ![]() para
para
![]() , si
, si ![]() describe un camino cualquiera en el semi-plano superior a partir de
describe un camino cualquiera en el semi-plano superior a partir de ![]() ,
, ![]() permanecerá también en este semi-plano, de otra forma
permanecerá también en este semi-plano, de otra forma ![]() atravesaría el eje real en el punto
atravesaría el eje real en el punto ![]() y la ecuación
y la ecuación ![]() tendría una raíz imaginaria. Por otra parte
tendría una raíz imaginaria. Por otra parte ![]() tiene coeficientes reales. Entonces
tiene coeficientes reales. Entonces ![]() define una substitución en el círculo fundamental y de la primera especie.
define una substitución en el círculo fundamental y de la primera especie.
Ahora supongamos que todos los puntos dobles están sobre la circunferencia, y que sus multiplicadores son reales y mayores que ![]() , en valor algebráico, para
, en valor algebráico, para ![]() de entre ellos, pero real y comprendido entre
de entre ellos, pero real y comprendido entre ![]() y
y ![]() para el
para el
![]() como resulta de la relación
como resulta de la relación
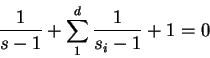
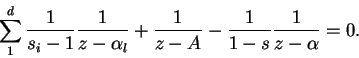
Tenemos aún
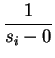
![]() . Consideremos los
. Consideremos los ![]() intervalos determinados por
intervalos determinados por ![]() números
números
![]() excluyendo toda vez a aquel, si hay uno, que contenga a
excluyendo toda vez a aquel, si hay uno, que contenga a ![]() . En los
. En los ![]() intervalos restantes, el primer miembro es continuo salvo en los dos extremos donde se anula una vez debido a que pasa de
intervalos restantes, el primer miembro es continuo salvo en los dos extremos donde se anula una vez debido a que pasa de ![]() a
a ![]() ; entonces las
; entonces las ![]() raíces son reales lo mismo que
raíces son reales lo mismo que ![]() . Terminamos el razonamiento como antes señalando que
. Terminamos el razonamiento como antes señalando que ![]() , definida por
, definida por
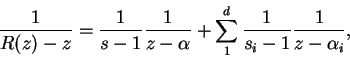
Consideremos finalmente el caso donde damos sobre la circunferencia un punto doble ![]() para el cual
para el cual
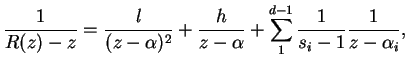 |
|||
 |
Vemos que ![]() permanece indeterminada. Si suponemos a las
permanece indeterminada. Si suponemos a las ![]() sobre el eje real, para que
sobre el eje real, para que ![]() deje esta recta invariante, falta que
deje esta recta invariante, falta que ![]() sea real. Tenemos además, en la vecindad de
sea real. Tenemos además, en la vecindad de ![]() ,
,
Suponer a ![]() real lleva a suponer que la tangente a
real lleva a suponer que la tangente a ![]() coincide con la tangente de rebotadura (rebroussement) a la curva que limita el dominio de convergencia elemental relativo a
coincide con la tangente de rebotadura (rebroussement) a la curva que limita el dominio de convergencia elemental relativo a ![]() (
(![]() ). Bajo esta forma, la condición es invariante con relación a toda transformación conforme3.1. Si es satisfecha, aún vemos fácilmente que
). Bajo esta forma, la condición es invariante con relación a toda transformación conforme3.1. Si es satisfecha, aún vemos fácilmente que ![]() pertenece a la clase que estudiamos y define una substitución singular de primer tipo. El procedimiento es siempre el mismo. Tenemos que demostrar que
pertenece a la clase que estudiamos y define una substitución singular de primer tipo. El procedimiento es siempre el mismo. Tenemos que demostrar que

Dejaremos de lado el caso donde se tiene
Finalmente, para las substituciones de segundo tipo, tendremos resultados semejantes. Por ejemplo, si damos ![]() puntos dobles sobre la circunferencia con
puntos dobles sobre la circunferencia con ![]() en valor algebráico, tendremos para la fórmula de descomposición en elementos simples una expresión de
en valor algebráico, tendremos para la fórmula de descomposición en elementos simples una expresión de ![]() que dará una subsitución de segundo tipo y de la primera especie.
que dará una subsitución de segundo tipo y de la primera especie.
Puede ser favorable elegir como círculo fundamental ![]() al círculo unitario
al círculo unitario
![]() . Pasemos de este círculo al semi-plano superior del plano de las
. Pasemos de este círculo al semi-plano superior del plano de las ![]() por la transformación
por la transformación
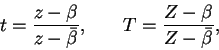
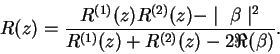
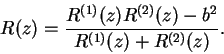
Supongamos en particular que ![]() tuviera el origen por punto doble;
tuviera el origen por punto doble;
![]() siendo holomorfa en el origen, e igual en módulo a la unidad para
siendo holomorfa en el origen, e igual en módulo a la unidad para
![]() , será más pequeña, en módulo, que la unidad para
, será más pequeña, en módulo, que la unidad para
![]() . Entonces
. Entonces ![]()
![]() deja
deja ![]() invariante. Tomemos
invariante. Tomemos
![]() y
y
![]() ; les corresponden las funciones
; les corresponden las funciones
![]() y
y
![]() . Tenemos entonces
. Tenemos entonces
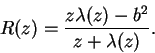
Vamos a deducir de esta fórmula una consecuencia importante a saber que
![]() es superior a la unidad sobre la circunferencia
es superior a la unidad sobre la circunferencia ![]() . Tenemos en efecto
. Tenemos en efecto
![\begin{displaymath}
\Phi'(t) = R'(z)\left[ \frac{z + bi}{R(z) + bi} \right]^2 .
\end{displaymath}](img1058.png)
Encontramos para ![]() la expresión
la expresión
![\begin{displaymath}
R'(z) =\frac{\lambda'(z)(z^2 + b^2) + b^2 + \lambda^2(z)}{[z + \lambda(z)]^2}
\end{displaymath}](img1060.png)
Reemplazando ![]() y
y ![]() por sus valores en función de
por sus valores en función de ![]() en la expresión de
en la expresión de ![]() , encontramos después de algunas reducciones
, encontramos después de algunas reducciones
![\begin{displaymath}
\Phi'(t) = \frac{\lambda'(z)(z^2 + b^2) + \lambda^2(z) + b^2}{[\lambda(z) + bi]^2}.
\end{displaymath}](img1063.png)
Para
![]() ,
, ![]() es real al igual que
es real al igual que ![]() ; tenemos entonces
; tenemos entonces

Conocemos la expresión de ![]() :
:
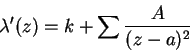
![]() es entonces positiva para
es entonces positiva para ![]() real. La expresión de
real. La expresión de
![]() muestra entonces que
muestra entonces que
![]() . Se afirma que jamás tendremos
. Se afirma que jamás tendremos
![]() . Para ello faltaría que
. Para ello faltaría que ![]() ó
ó ![]() llegarán a ser infinitas. Ahora bien, cuando
llegarán a ser infinitas. Ahora bien, cuando ![]() llega a coincidir con un polo
llega a coincidir con un polo ![]() , encontramos que el valor límite de
, encontramos que el valor límite de ![]() es igual a
es igual a ![]()
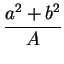
![]() . Para
. Para ![]() , obtenemos el valor límite
, obtenemos el valor límite
![]() si
si ![]() no es nulo, y
no es nulo, y ![]()
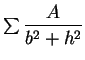 si
si ![]() .
.
Entonces siempre tenemos
Las consideraciones anteriores permiten resolver el problema límite de la iteración, es decir encontrar el conjunto obtenido de los consecuentes de un punto, por la substitución de las diversas especies que hemos considerado.
Consideremos primero una substitución de primer tipo y de primera especie. La cual admite dos puntos dobles atractores que supondremos están, como antes, en el origen y en el punto en el infinito, el círculo ![]() siendo
siendo
![]() .
.
Sea ![]() esta substitución. Se tiene que los consecuentes de todo punto situado en el círculo
esta substitución. Se tiene que los consecuentes de todo punto situado en el círculo ![]() concéntrico a
concéntrico a ![]() de radio más pequeño tienden uniformemente a cero. En efecto, el módulo máximo para
de radio más pequeño tienden uniformemente a cero. En efecto, el módulo máximo para
![]() de
de
![]() siendo una función creciente cuando
siendo una función creciente cuando ![]() varía de
varía de ![]() a
a ![]() para
para
![]() , tenemos uniformemente
, tenemos uniformemente
Inversamente, dado un conjunto cerrado cualquiera ![]() los
antecedentes de todo punto de
los
antecedentes de todo punto de ![]() tienden uniformemente hacia la
circunferencia, suponiendo que
tienden uniformemente hacia la
circunferencia, suponiendo que ![]() no contiene los puntos dobles
no contiene los puntos dobles ![]() e
e ![]() . Pues, si fuera de otra manera, habría antecedentes de
diversos puntos de
. Pues, si fuera de otra manera, habría antecedentes de
diversos puntos de ![]() de rango indefinidamente creciente, exteriores
a la corona
de rango indefinidamente creciente, exteriores
a la corona ![]() e interiores, por ejemplo, al círculo
e interiores, por ejemplo, al círculo
![]() . Sean
. Sean
![]() estos antecedentes, tendríamos entonces:
estos antecedentes, tendríamos entonces:
![\begin{displaymath}
\begin{array}{rcl}
R_{n_1}(z') & = & \xi', \\
R_{n_2}(z'') ...
... \\
&\vdots &\\
R_{n_p}[z^{(p)}] & = & \xi^{(p)}.
\end{array}\end{displaymath}](img1084.png)
Podemos precisar más la manera en que los antecedentes de un punto se aproximan a la circunferencia.
Consideremos la circunferencia ![]() de centro
de centro ![]() y de radio
y de radio ![]() . Se cumple que si
. Se cumple que si ![]() es suficientemente cercano a
es suficientemente cercano a ![]() , las diferentes ramas de
, las diferentes ramas de ![]() se permutan circularmente cuando
se permutan circularmente cuando ![]() describe
describe ![]() . Supongamos a
. Supongamos a ![]() superior en módulo a todas las raíces de
superior en módulo a todas las raíces de ![]() , y sea
, y sea ![]() la curva (comprendida entre
la curva (comprendida entre ![]() y
y ![]() ) descrita por una determinación de
) descrita por una determinación de ![]() cuando
cuando ![]() describe a
describe a
![]() se cierra cuando
se cierra cuando ![]() describe
describe ![]() veces
veces ![]() ; recíprocamente, si
; recíprocamente, si ![]() describe
describe ![]() una sola vez,
una sola vez, ![]() describe
describe ![]() veces
veces ![]() en el sentido directo, su argumento aumenta en
en el sentido directo, su argumento aumenta en
![]() el cual debe representar el número de ceros de
el cual debe representar el número de ceros de ![]() comprendida en el interior de
comprendida en el interior de ![]() , multiplicada por
, multiplicada por ![]() . Entonces este número es al menos
. Entonces este número es al menos ![]() (ya que
(ya que ![]() ); entonces
); entonces ![]() , rodea el origen y, por consecuencia, ya que es exterior a
, rodea el origen y, por consecuencia, ya que es exterior a ![]() , todos los puntos raíces de
, todos los puntos raíces de ![]() . Tenemos
. Tenemos ![]() , grado de
, grado de ![]() , y las
, y las ![]() ramas de
ramas de ![]() se permutan circularmente cuando
se permutan circularmente cuando ![]() describe
describe ![]() ; esto subsiste cuando deformamos
; esto subsiste cuando deformamos ![]() sin atravesar los puntos críticos de
sin atravesar los puntos críticos de ![]() .
.
Consideremos entonces la corona
![]() que no contiene punto crítico alguno de
que no contiene punto crítico alguno de ![]() , ni por consecuencia de
, ni por consecuencia de ![]() , y tracemos un corte, por ejemplo, siguiendo un radio; los
, y tracemos un corte, por ejemplo, siguiendo un radio; los ![]() llegan a ser uniformes en el dominio así obtenido
llegan a ser uniformes en el dominio así obtenido ![]() . Los antecedentes
. Los antecedentes ![]() del dominio
del dominio ![]() son cuadriláteros curvilineos yuxtapuestos en la corona comprendida entre
son cuadriláteros curvilineos yuxtapuestos en la corona comprendida entre ![]() y
y ![]() ; los antecedentes
; los antecedentes ![]() del dominio
del dominio ![]() , es decir los antecedentes inmediatos de los
, es decir los antecedentes inmediatos de los ![]() , son cuadrilateros curvilíneos yuxtapuestos en la corona comprendida entre
, son cuadrilateros curvilíneos yuxtapuestos en la corona comprendida entre ![]() y
y ![]() y así sucesivamente, las curvas
y así sucesivamente, las curvas
![]() desarrollandose mutuamente y tendiendo hacia
desarrollandose mutuamente y tendiendo hacia ![]() . Se afirma que las dimensiones lineales de las
. Se afirma que las dimensiones lineales de las ![]() tienden hacia cero junto con
tienden hacia cero junto con ![]() ; ya que la diferencial del arco del contorno de
; ya que la diferencial del arco del contorno de ![]() está designada por
está designada por ![]() tenemos para un delta
tenemos para un delta ![]() y un
y un
![]() convenientemente asociados
convenientemente asociados
Los mismos fenómenos se producen para el exterior del círculo en razón de la simetría con relación al círculo. Entonces el ![]() -ésimo consecuente de un dominio circular de radio tan pequeño como lo queramos, teniendo su centro en un punto cualquiera de la circunferencia
-ésimo consecuente de un dominio circular de radio tan pequeño como lo queramos, teniendo su centro en un punto cualquiera de la circunferencia ![]() , cubrirá para un valor finito de
, cubrirá para un valor finito de ![]() toda una corona de grosor finito rodeando
toda una corona de grosor finito rodeando ![]() . Pero los consecuentes de orden
. Pero los consecuentes de orden ![]() de esta corona recubrirán todo el plano para un valor finito de
de esta corona recubrirán todo el plano para un valor finito de ![]() , excepto quizá el entorno de los dos puntos dobles
, excepto quizá el entorno de los dos puntos dobles ![]() e
e ![]() , esta última excepción produciendose solamente si estos puntos no tienen más antecedente que ellos mismos, es decir son puntos excepcionales de los cuales hemos hablado en el Capítulo I; esto no tendrá lugar mas que para
, esta última excepción produciendose solamente si estos puntos no tienen más antecedente que ellos mismos, es decir son puntos excepcionales de los cuales hemos hablado en el Capítulo I; esto no tendrá lugar mas que para ![]() . De lo que se puede concluir:
. De lo que se puede concluir:
![]() El consecuente de orden
El consecuente de orden ![]() de un dominio arbitrariamente pequeño rodeando un punto de la circunferencia cubrirá todo el plano para un valor finito de
de un dominio arbitrariamente pequeño rodeando un punto de la circunferencia cubrirá todo el plano para un valor finito de ![]() (excepto, en el caso donde
(excepto, en el caso donde ![]() , el interior de un círculo de radio arbitrariamente pequeño y el exterior de un círculo arbitrariamente grande de centro
, el interior de un círculo de radio arbitrariamente pequeño y el exterior de un círculo arbitrariamente grande de centro ![]() );
);
![]() El consecuente de orden
El consecuente de orden ![]() de un arco tan pequeño como se quiera de la circunferencia la recubrirá completamente para un valor finito de
de un arco tan pequeño como se quiera de la circunferencia la recubrirá completamente para un valor finito de ![]() .
.
Así el conjunto derivado de los antecedentes de un punto cualquiera del plano (salvo los dos puntos excepcionales, si existen) está formado por toda la circunferencia.
Conocemos entonces el conjunto derivado de los antecedentes y de los consecuentes de un punto del plano de una manera muy precisa, salvo él de los consecuentes de un punto de la circunferencia; la búsqueda del conjunto derivado de los consecuentes de un punto de ![]() es un problema de naturaleza aritmética que se relaciona a la aproximación de los inconmensurables y que no buscaremos a profundidad aquí. Solamente mostraremos, sobre ejemplos, cuales son las principales circunstancias que pueden presentarse.
es un problema de naturaleza aritmética que se relaciona a la aproximación de los inconmensurables y que no buscaremos a profundidad aquí. Solamente mostraremos, sobre ejemplos, cuales son las principales circunstancias que pueden presentarse.
Consideremos entonces los consecuentes de un punto ![]() de
de ![]() ; estos puntos son todos distintos a menos que
; estos puntos son todos distintos a menos que ![]() sea el antecedente de un punto doble o periódico; tales antecedentes son densos sobre
sea el antecedente de un punto doble o periódico; tales antecedentes son densos sobre ![]() y para cada uno de ellos el conjunto
y para cada uno de ellos el conjunto ![]() derivado de los consecuentes de
derivado de los consecuentes de ![]() puede ser visto como formado por los puntos de un ciclo, o como no conteniendo ningún punto, según veamos, formando parte o no de
puede ser visto como formado por los puntos de un ciclo, o como no conteniendo ningún punto, según veamos, formando parte o no de ![]() los puntos donde son iguales una infinidad de consecuentes. Éste es en general el primer punto de vista que parece ser el más natural de adoptar.
los puntos donde son iguales una infinidad de consecuentes. Éste es en general el primer punto de vista que parece ser el más natural de adoptar.
Voy a demostrar que los mismos puntos periódicos son densos sobre ![]() . En efecto, siendo
. En efecto, siendo ![]() un arco cualquiera de
un arco cualquiera de ![]() , existe una rama de la función
, existe una rama de la función ![]() , para
, para ![]() suficientemente grande, que da como imagen de
suficientemente grande, que da como imagen de ![]() el arco
el arco ![]() , completamente interior a
, completamente interior a ![]() cuando transformamos por
cuando transformamos por ![]() el arco
el arco ![]() y el arco
y el arco ![]() , que ahí está contenido, obtenemos como imagen de
, que ahí está contenido, obtenemos como imagen de ![]() un arco
un arco ![]() interior a
interior a ![]() ; el arco
; el arco ![]() tendrá en su contorno una transformada
tendrá en su contorno una transformada ![]() y así sucesivamente; los arcos
y así sucesivamente; los arcos ![]() encajados los unos en los otros y de longitudes tendiendo a cero como los términos de una progresión geométrica convergente tienden hacia un punto
encajados los unos en los otros y de longitudes tendiendo a cero como los términos de una progresión geométrica convergente tienden hacia un punto ![]() ; como siempre se tiene simbólicamente
; como siempre se tiene simbólicamente
El punto ![]() forma parte entonces de un ciclo cuyo orden es un divisor de
forma parte entonces de un ciclo cuyo orden es un divisor de ![]() ; con el arco
; con el arco ![]() siendo arbitrario, vemos que todo punto de
siendo arbitrario, vemos que todo punto de ![]() es punto periódico o límite de puntos periódicos; siempre es límite de puntos periódicos y de periodo indefinidamente creciente ya que no hay un número finito de tales puntos cuyo periodo no sobrepase un número dado.
es punto periódico o límite de puntos periódicos; siempre es límite de puntos periódicos y de periodo indefinidamente creciente ya que no hay un número finito de tales puntos cuyo periodo no sobrepase un número dado.
Podemos señalar que aquí siempre hay puntos de periodo ![]() cualquiera que sea
cualquiera que sea ![]() ; en efecto, como no hay puntos periódicos cuyo multiplicador sea de la forma
; en efecto, como no hay puntos periódicos cuyo multiplicador sea de la forma
![]() , el caso de excepción examinado en el parágrafo 3 no se presenta y las ecuaciones
, el caso de excepción examinado en el parágrafo 3 no se presenta y las ecuaciones ![]() no tienen más que raíces simples. El número
no tienen más que raíces simples. El número ![]() de los puntos periódicos de orden
de los puntos periódicos de orden ![]() se obtienen entonces haciendo la inversión de la fórmula
se obtienen entonces haciendo la inversión de la fórmula

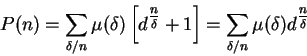
Tenemos entonces en todo arco de ![]() una infinidad numerable de puntos periódicos para los cuales por consiguiente
una infinidad numerable de puntos periódicos para los cuales por consiguiente ![]() se reduce a un número finito de puntos.
se reduce a un número finito de puntos.
Vamos a mostrar que podemos encontrar igualmente en todo arco de ![]() puntos para los cuales
puntos para los cuales ![]() está formado por la circunferencia completa. Consideremos una infinidad numerable de arcos de
está formado por la circunferencia completa. Consideremos una infinidad numerable de arcos de ![]() sea
sea
![]() que escribiremos en el siguiente orden, tal que cada uno de ellos figure una infinidad de veces:
que escribiremos en el siguiente orden, tal que cada uno de ellos figure una infinidad de veces:
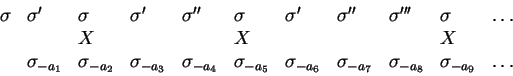
Los arcos
Hay así puntos de ![]() en
en
![]() ; si estos arcos han sido elegidos de manera que hubiera una infinidad que fueran completamente exteriores unos de otros,
; si estos arcos han sido elegidos de manera que hubiera una infinidad que fueran completamente exteriores unos de otros, ![]() contendría una infinidad de puntos.
contendría una infinidad de puntos.
Para fijar las ideas, consideremos la infinidad numerable de los arcos que tienen por término medio los puntos de argumento
![]() y de longitud
y de longitud
![]() , tomando todos los pares de enteros
, tomando todos los pares de enteros ![]() y
y ![]() tales que
tales que ![]() , no primos entre ellos; habrá puntos de
, no primos entre ellos; habrá puntos de ![]() en todos los arcos que tienen por mitad un punto dado
en todos los arcos que tienen por mitad un punto dado
![]() y una longitud
y una longitud
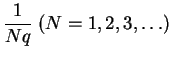 ; este punto es entonces de
; este punto es entonces de ![]() o límite de puntos de
o límite de puntos de ![]() ; pues bien es
; pues bien es ![]() el cual es cerrado y comprende así toda la circunferencia ya que encierra todos los puntos de argumento comensurable a
el cual es cerrado y comprende así toda la circunferencia ya que encierra todos los puntos de argumento comensurable a ![]() .
.
Así ![]() puede comprender toda la circunferencia o estar formado de un número finito de puntos. Pueden producirse casos intermedios; pero es conveniente señalar que
puede comprender toda la circunferencia o estar formado de un número finito de puntos. Pueden producirse casos intermedios; pero es conveniente señalar que ![]() siendo un conjunto invariante que comprende los consecuentes de todos sus puntos comprenderá toda la circunferencia si comprende un arco tan pequeño como queramos. Si lo anterior no tiene lugar,
siendo un conjunto invariante que comprende los consecuentes de todos sus puntos comprenderá toda la circunferencia si comprende un arco tan pequeño como queramos. Si lo anterior no tiene lugar, ![]() es por todas partes, discontinuo. Vamos a mostrar sobre un ejemplo que
es por todas partes, discontinuo. Vamos a mostrar sobre un ejemplo que ![]() puede ser un conjunto perfecto discontinuo. Consideremos la substitución
puede ser un conjunto perfecto discontinuo. Consideremos la substitución ![]() , y un punto
, y un punto ![]() de argumento
de argumento ![]() sobre la circunferencia
sobre la circunferencia ![]() tal que
tal que
![]() se escribe en el sistema de numeración de base
se escribe en el sistema de numeración de base ![]() no empleando más que las cifras
no empleando más que las cifras ![]() y
y ![]() ;
;
![]() pertenece entonces al conjunto perfecto
pertenece entonces al conjunto perfecto ![]() , ejemplo clásico debido a Cantor de un conjunto perfecto que no es denso en ningún intervalo. Los valores de
, ejemplo clásico debido a Cantor de un conjunto perfecto que no es denso en ningún intervalo. Los valores de
![]() correspondiendo a los consecuentes del punto de
correspondiendo a los consecuentes del punto de ![]() se obtienen desplazando la coma hacia la derecha y, anulando la parte entera en el desarrollo que corresponde al punto inicial; los números obtenidos pertenecen siempre a
se obtienen desplazando la coma hacia la derecha y, anulando la parte entera en el desarrollo que corresponde al punto inicial; los números obtenidos pertenecen siempre a ![]() . Llamemos
. Llamemos ![]() al conjunto perfecto de puntos de la circunferencia que corresponde a
al conjunto perfecto de puntos de la circunferencia que corresponde a ![]() ; los puntos de
; los puntos de ![]() siendo de
siendo de ![]() , al igual que los puntos de
, al igual que los puntos de ![]() ya que
ya que ![]() es perfecto. Podemos elegir
es perfecto. Podemos elegir ![]() de manera que
de manera que ![]() sea idéntica a
sea idéntica a ![]() . Consideremos los números que se escriben empleando solamente las cifras
. Consideremos los números que se escriben empleando solamente las cifras ![]() y
y ![]() un número finito de veces y son ordenados en una serie lineal tal que cada uno de ellos figure una infinidad de veces:
un número finito de veces y son ordenados en una serie lineal tal que cada uno de ellos figure una infinidad de veces:
![]() . Basta establecer
. Basta establecer
Podemos formar de una manera análoga ejemplos donde ![]() es un conjunto reducible. Pero
es un conjunto reducible. Pero ![]() resulta de lo que hemos visto en el parágrafo 15 que un conjunto cerrado y además invariante para la substitución dada sobre la circunferencia, este conjunto no será en general el derivado de los consecuentes de un punto; ya que el conjunto formado por dos puntos dobles distintos es un conjunto cerrado e invariante y sabemos que si un conjunto
resulta de lo que hemos visto en el parágrafo 15 que un conjunto cerrado y además invariante para la substitución dada sobre la circunferencia, este conjunto no será en general el derivado de los consecuentes de un punto; ya que el conjunto formado por dos puntos dobles distintos es un conjunto cerrado e invariante y sabemos que si un conjunto ![]() encierrra estos dos puntos, encierra una infinidad del resto.
encierrra estos dos puntos, encierra una infinidad del resto.
Bastan estos ejemplos para mostrar que el estudio del conjunto ![]() es un problema de naturaleza aritmética al cual podríamos aplicar los métodos de Borel-Lebesgue para la medida de los conjuntos, y que reclaman de nuevas investigaciones; pero en todos los casos hemos probado superabundantemente que los puntos límites de los consecuentes de un punto
es un problema de naturaleza aritmética al cual podríamos aplicar los métodos de Borel-Lebesgue para la medida de los conjuntos, y que reclaman de nuevas investigaciones; pero en todos los casos hemos probado superabundantemente que los puntos límites de los consecuentes de un punto ![]() de la circunferencia son funciones discontinuas de
de la circunferencia son funciones discontinuas de ![]() en cada punto de ésta.
en cada punto de ésta.
Pasamos ahora al estudio de las substituciones de primer tipo y de segunda especie. Estando confinado el punto doble atractor al infinito, podemos establecer
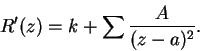
Tenemos entonces sobre el eje real
Estableciendo
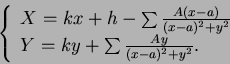
Tenemos constantemente
En toda la región ![]() del plano exterior al rectángulo y sobre el contorno, tenemos
del plano exterior al rectángulo y sobre el contorno, tenemos
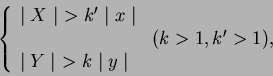
Lo mismo tiene lugar para las ![]() curvas distintas
curvas distintas
![]() . Estas curvas son entonces exteriores unas de otras , pues si un punto
. Estas curvas son entonces exteriores unas de otras , pues si un punto ![]() estuviera por ejemplo a la vez en el interior de
estuviera por ejemplo a la vez en el interior de ![]() y sobre el contorno
y sobre el contorno ![]() , tendríamos a la vez
, tendríamos a la vez ![]() interior a
interior a ![]() y
y ![]() sobre
sobre ![]() .
.
Consideremos el interior de ![]() con la curvas
con la curvas
![]() , (tomando por ejemplo
, (tomando por ejemplo ![]() ) y haciendo de nuevo la aplicación de esta figura sobre
) y haciendo de nuevo la aplicación de esta figura sobre ![]() , después sobre
, después sobre ![]() , después sobre
, después sobre ![]() . El interior de
. El interior de ![]() siendo aplicable de una manera biunívoca sobre el interior de
siendo aplicable de una manera biunívoca sobre el interior de ![]() , a las tres curvas
, a las tres curvas
![]() corresponderán tres nuevas curvas interiores a
corresponderán tres nuevas curvas interiores a ![]() y al interior de las primeras curvas el interior de las segundas. Sean
y al interior de las primeras curvas el interior de las segundas. Sean
![]() estas tres nuevas curvas. Obtendremos de igual forma, con la aplicación de
estas tres nuevas curvas. Obtendremos de igual forma, con la aplicación de ![]() sobre
sobre ![]() , las tres curvas
, las tres curvas
![]() interiores a
interiores a ![]() . Finalmente aplicando
. Finalmente aplicando ![]() sobre
sobre ![]() , obtenemos
, obtenemos
![]() interiores a
interiores a ![]() . Las curvas
. Las curvas ![]() limitan así nueve dominios acotados sin punto en común cuyo conjunto constituye la región antecedente de orden
limitan así nueve dominios acotados sin punto en común cuyo conjunto constituye la región antecedente de orden ![]() del interior de
del interior de ![]() . De una manera general, el antecedente de orden
. De una manera general, el antecedente de orden ![]() del interior de
del interior de ![]() estará formado por el interior de
estará formado por el interior de ![]() curvas:
curvas:
En el caso que nos ocupa, todas estas curvas cortan el eje real en dos puntos ya que todos los antecedentes de un punto real son reales.
El dominio abierto de convergencia de las ![]() hacia el infinito es el conjunto de los puntos perteneciendo a todos los dominios
hacia el infinito es el conjunto de los puntos perteneciendo a todos los dominios
Entre las longitudes finitas de las curvas ![]() y
y ![]() , tenemos la misma relación:
, tenemos la misma relación:
Las longitudes de las curvas ![]() tienden hacia cero con
tienden hacia cero con
![]() . Por otra parte, toda curva
. Por otra parte, toda curva ![]() encierra curvas de rangos
encierra curvas de rangos
![]() respectivamente, de las cuales cada una es interior a la anterior; existe entonces un punto interior común que pertenece a
respectivamente, de las cuales cada una es interior a la anterior; existe entonces un punto interior común que pertenece a ![]() .
.
Así los puntos de ![]() pueden estar encerrados en el interior de un número finito de curvas, a saber las
pueden estar encerrados en el interior de un número finito de curvas, a saber las ![]() curvas
curvas ![]() de las cuales cada una tiene una longitud tan pequeña como queramos para
de las cuales cada una tiene una longitud tan pequeña como queramos para ![]() suficientemente grande y que contiene todos o al menos uno de los puntos. De lo anterior se sigue que
suficientemente grande y que contiene todos o al menos uno de los puntos. De lo anterior se sigue que ![]() es perfecto y discontinuo en cada punto. Primero
es perfecto y discontinuo en cada punto. Primero ![]() es cerrada, pues si
es cerrada, pues si ![]() punto límite de los puntos
punto límite de los puntos
![]() de
de ![]() no perteneciera a
no perteneciera a ![]() ,
, ![]() sería para un cierto valor de
sería para un cierto valor de ![]() exterior a todas las curvas
exterior a todas las curvas ![]() ; siendo entonces
; siendo entonces ![]() la distancia más corta de
la distancia más corta de ![]() a las curvas
a las curvas ![]() y los puntos
y los puntos
![]() siendo interiores a las
siendo interiores a las ![]() , la distancia de
, la distancia de ![]() a
a
![]() sería mayor o igual a
sería mayor o igual a ![]() ;
; ![]() no sería entonces punto límite de
no sería entonces punto límite de ![]() .
. ![]() es perfecto, pues estando
es perfecto, pues estando ![]() encerrada en una curva
encerrada en una curva ![]() y a su vez esta encerrando en su interior al menos dos curvas distintas y exteriores una de otra
y a su vez esta encerrando en su interior al menos dos curvas distintas y exteriores una de otra ![]() ,
, ![]() estará contenida igualmente en una de éstas últimas, sea
estará contenida igualmente en una de éstas últimas, sea ![]() . Pero otra curva
. Pero otra curva
![]() igualmente interior a
igualmente interior a ![]() contiene al menos un punto
contiene al menos un punto ![]() de
de ![]() necesariamente distinto de
necesariamente distinto de ![]() y la distancia
y la distancia ![]() es inferior al diámetro
es inferior al diámetro ![]() de la curva
de la curva ![]() que es tan pequeña como queramos para
que es tan pequeña como queramos para ![]() suficientemente grande.
suficientemente grande. ![]() es discontinua en cada punto, ya que si
es discontinua en cada punto, ya que si ![]() y
y ![]() son dos puntos de
son dos puntos de ![]() , podemos encerrarlos en curvas
, podemos encerrarlos en curvas ![]() cuyo diámetro sea inferior a la semi-distancia de
cuyo diámetro sea inferior a la semi-distancia de ![]() ;
; ![]() y
y ![]() son entonces encerrados en dos curvas
son entonces encerrados en dos curvas ![]() y
y ![]() distintas y exteriores una de la otra y toda línea poligonal uniendo
distintas y exteriores una de la otra y toda línea poligonal uniendo ![]() y teniendo por vértices puntos de
y teniendo por vértices puntos de ![]() tendrá al menos un lado igual a la distancia más corta de una de las curvas
tendrá al menos un lado igual a la distancia más corta de una de las curvas ![]() en el conjunto
en el conjunto ![]() , o a la distancia más corta de dos curvas
, o a la distancia más corta de dos curvas ![]() .
.
En el caso actual, al conjunto ![]() pertenece por completo al eje real ya que todas las curvas
pertenece por completo al eje real ya que todas las curvas ![]() cortan el eje real en dos puntos.
cortan el eje real en dos puntos.
La elección es evidente a priori ya que hemos visto al inicio de este análisis que ![]() tiende hacia el infinito cuando
tiende hacia el infinito cuando ![]() es imaginaria y que el conjunto
es imaginaria y que el conjunto ![]() es el conjunto de puntos para los cuales esta convergencia no tiene lugar. Habríamos podido servirnos de esta observación para construir el conjunto
es el conjunto de puntos para los cuales esta convergencia no tiene lugar. Habríamos podido servirnos de esta observación para construir el conjunto ![]() . En efecto, consideremos la raíz más grande (real)
. En efecto, consideremos la raíz más grande (real) ![]() de la ecuación
de la ecuación ![]() , comprendida entre el último polo
, comprendida entre el último polo ![]() hacia la derecha y
hacia la derecha y ![]() , y de igual manera la más pequeña raíz
, y de igual manera la más pequeña raíz ![]() comprendida entre el último polo
comprendida entre el último polo ![]() hacia la izquierda y
hacia la izquierda y ![]() , y veamos el conjunto de las dos semi-rectas
, y veamos el conjunto de las dos semi-rectas
![]() y
y
![]() como constituyendo un segmento único conteniendo el punto en el infinito. En este segmento,
como constituyendo un segmento único conteniendo el punto en el infinito. En este segmento, ![]() converge hacia el infinito (excepto en los extremos). Pues, para
converge hacia el infinito (excepto en los extremos). Pues, para ![]() , tenemos
, tenemos
![]() , y para
, y para
![]() (en valor algebráico) y
(en valor algebráico) y
Los puntos del eje real que pertenecen al dominio ![]() de convergencia hacia el infinito son el segmento
de convergencia hacia el infinito son el segmento ![]() y sus antecedentes, extremos no comprendidos; tenemos así una infinidad numerable de intervalos sin puntos en común de dos a dos y sin extremos comunes, contiguos a un conjunto perfecto que es el conjunto
y sus antecedentes, extremos no comprendidos; tenemos así una infinidad numerable de intervalos sin puntos en común de dos a dos y sin extremos comunes, contiguos a un conjunto perfecto que es el conjunto ![]() del cual probaremos fácilmente la discontinuidad. Pero el análisis anterior es preferible por que es aplicable a casos donde
del cual probaremos fácilmente la discontinuidad. Pero el análisis anterior es preferible por que es aplicable a casos donde ![]() no es lineal.
no es lineal.
Consideremos un punto ![]() de
de ![]() y un círculo
y un círculo ![]() de radio
de radio ![]() teniendo por centro
teniendo por centro ![]() . Para un valor conveniente del entero
. Para un valor conveniente del entero ![]() , el diámetro de las curvas
, el diámetro de las curvas ![]() será inferior a
será inferior a ![]() ; el círculo
; el círculo ![]() conteniendo
conteniendo ![]() contendrá entonces un dominio
contendrá entonces un dominio ![]() acotado por una curva
acotado por una curva ![]() y que es un antecedente de rango
y que es un antecedente de rango ![]() del interior de
del interior de ![]() de la curva
de la curva ![]() . El
. El ![]() -ésimo consecuente del círculo
-ésimo consecuente del círculo ![]() cubrirá entonces
cubrirá entonces ![]() . Por otra parte, siendo
. Por otra parte, siendo ![]() el complemento del dominio (abierto)
el complemento del dominio (abierto) ![]() ,
,
![]() recubre todo el plano; como
recubre todo el plano; como ![]() para
para ![]() suficientemente grande es exterior a un círculo de radio tan grande como queramos,
suficientemente grande es exterior a un círculo de radio tan grande como queramos, ![]() cubrirá todo el plano excepto quizá el exterior de este círculo; pero
cubrirá todo el plano excepto quizá el exterior de este círculo; pero
![]() contiene
contiene ![]() , si
, si ![]() , y como
, y como ![]() encierra un polo
encierra un polo ![]() , contiene el exterior de un cierto círculo de centro
, contiene el exterior de un cierto círculo de centro ![]() . Entonces
. Entonces ![]() para
para ![]() suficientemente grande cubre todo el plano. Como
suficientemente grande cubre todo el plano. Como ![]() cubre
cubre ![]() ,
, ![]() cubre todo el plano. Así:
cubre todo el plano. Así:
El
![]() consecuente de un dominio tan pequeño como lo queramos rodeando un punto de
consecuente de un dominio tan pequeño como lo queramos rodeando un punto de ![]() cubre todo el plano para un valor finito de
cubre todo el plano para un valor finito de ![]() .
.
Todo punto de ![]() es así límite de los antecedentes de un punto cualquiera del plano. Veamos por otra parte inmediatamente que
es así límite de los antecedentes de un punto cualquiera del plano. Veamos por otra parte inmediatamente que ![]() contiene los consecuentes y antecedentes de todos sus puntos. Contiene también los puntos dobles y periódicos además de
contiene los consecuentes y antecedentes de todos sus puntos. Contiene también los puntos dobles y periódicos además de ![]() . Aún podremos demostrar que
. Aún podremos demostrar que ![]() es límite de puntos periódicos; que contiene, puntos tales que el conjunto derivado de sus consecuentes sea idéntico a
es límite de puntos periódicos; que contiene, puntos tales que el conjunto derivado de sus consecuentes sea idéntico a ![]() , etc. No cabe insistir, pues encontraremos en el Capítulo siguiente (que será publicado posteriormente) teoremas más generales.
, etc. No cabe insistir, pues encontraremos en el Capítulo siguiente (que será publicado posteriormente) teoremas más generales.
Es interesante saber si ![]() es de medida lineal nula, esta propiedad interviene en el estudio de las funciones uniformes que admiten a
es de medida lineal nula, esta propiedad interviene en el estudio de las funciones uniformes que admiten a ![]() como conjunto de sus singularidades esenciales. Para que lo anterior tenga lugar basta que la suma de las longitudes de las curvas
como conjunto de sus singularidades esenciales. Para que lo anterior tenga lugar basta que la suma de las longitudes de las curvas ![]() tienda a cero con
tienda a cero con
![]() . Lo que sucederá siempre que tengamos
. Lo que sucederá siempre que tengamos ![]() [grado de
[grado de ![]() ], condición en absoluto necesaria. Además no alcanzé a reconocer si
], condición en absoluto necesaria. Además no alcanzé a reconocer si ![]() puede ser de medida no nula.
puede ser de medida no nula.
En resumen, dada una substitución en el círculo fundamental de segunda especie, los consecuentes de un punto cualquiera del plano convergen hacia el punto doble atractor situado sobre la circunferencia, exceptuando los puntos de un conjunto perfecto ![]() por todas partes discontinuo situado igualmente sobre la circunferencia; este conjunto que es invariante, goza de la propiedad de que cada uno de sus puntos es límite de los antecedentes de un punto cualquiera del plano. En todo dominio cerrado no conteniendo ningún punto en común con
por todas partes discontinuo situado igualmente sobre la circunferencia; este conjunto que es invariante, goza de la propiedad de que cada uno de sus puntos es límite de los antecedentes de un punto cualquiera del plano. En todo dominio cerrado no conteniendo ningún punto en común con ![]() , la convergencia es naturalmente uniforme.
, la convergencia es naturalmente uniforme.
Consideremos ahora el caso singular donde hay sobre la circunferencia un punto doble de multplicador igual a ![]() , contando por dos puntos dobles iguales. La substitución puede entonces llevarse a la forma
, contando por dos puntos dobles iguales. La substitución puede entonces llevarse a la forma
 |
|||
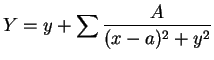 |
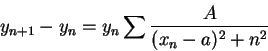
Hay entonces convergencia uniforme en toda parte acotada de un dominio definido por ![]() ó
ó ![]() . Sabemos que también hay convergencia en todo dominio cerrado definido por
. Sabemos que también hay convergencia en todo dominio cerrado definido por ![]() para
para ![]() suficientemente grande. Podríamos considerar el dominio de los puntos para los cuales tenemos una de estas tres desigualdades y buscar sus antecedentes sucesivos como en el parágrafo anterior. Nos conformaremos con examinar lo que sucede sobre el eje real. Sea
suficientemente grande. Podríamos considerar el dominio de los puntos para los cuales tenemos una de estas tres desigualdades y buscar sus antecedentes sucesivos como en el parágrafo anterior. Nos conformaremos con examinar lo que sucede sobre el eje real. Sea ![]() el último punto doble a distancia finita a la derecha de los polos
el último punto doble a distancia finita a la derecha de los polos ![]() , las
, las ![]() convergen hacia el infinito cuando
convergen hacia el infinito cuando ![]() es interior al segmento
es interior al segmento
![]() , y recíprocamente los consecuentes de todo punto
, y recíprocamente los consecuentes de todo punto ![]() tal que
tal que ![]() tienda hacia el infinito se encuentran a partir de un cierto rango en el interior de este segmento, a excepción de los antecedentes del punto en el infinito. El conjunto de los puntos
tienda hacia el infinito se encuentran a partir de un cierto rango en el interior de este segmento, a excepción de los antecedentes del punto en el infinito. El conjunto de los puntos ![]() del eje real para los cuales hay convergencia uniforme para las
del eje real para los cuales hay convergencia uniforme para las ![]() hacia el infinito es el conjunto de los puntos interiores al segmento
hacia el infinito es el conjunto de los puntos interiores al segmento
![]() y a todos sus antecedentes. Estos segmentos todos descritos en el mismo sentido [ya que
y a todos sus antecedentes. Estos segmentos todos descritos en el mismo sentido [ya que ![]() es positiva para
es positiva para ![]() real] entonces no tienen puntos en común de dos en dos y ni extremos comunes; son contiguos a un conjunto perfecto
real] entonces no tienen puntos en común de dos en dos y ni extremos comunes; son contiguos a un conjunto perfecto ![]() . Decimos que
. Decimos que ![]() es no denso, es decir que todo segmento conteniendo en su interior un punto de
es no denso, es decir que todo segmento conteniendo en su interior un punto de ![]() encierra antecedentes de puntos de
encierra antecedentes de puntos de ![]() . En efecto, si
. En efecto, si ![]() es un punto de
es un punto de ![]() que no sea un antecedente del punto en el infinito, sus consecuentes serán interiores una infinidad de veces a un segmento acotado, por ejemplo aquel que tiene por extremos el polo
que no sea un antecedente del punto en el infinito, sus consecuentes serán interiores una infinidad de veces a un segmento acotado, por ejemplo aquel que tiene por extremos el polo ![]() el más a la izquierda y el punto doble
el más a la izquierda y el punto doble ![]() . Pues si
. Pues si ![]() está a la izquierda de las
está a la izquierda de las ![]() , tenemos
, tenemos
Dicho lo anterior, tenemos
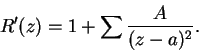
Sea entonces ![]() un segmento conteniendo el punto
un segmento conteniendo el punto ![]() . Si los segmentos consecuentes
. Si los segmentos consecuentes
![]() fueran constantemente exteriores a
fueran constantemente exteriores a ![]() , jamás contendrían polos
, jamás contendrían polos ![]() y serían todos descritos en el mismo sentido,
y serían todos descritos en el mismo sentido, ![]() y
y ![]() extremos de izquierda y de derecha de
extremos de izquierda y de derecha de ![]() ; siendo los consecuentes respectivos de
; siendo los consecuentes respectivos de ![]() y de
y de ![]() , extremos de izquierda y de derecha de
, extremos de izquierda y de derecha de ![]() ; las longitudes de los segmentos
; las longitudes de los segmentos ![]() creciendo constantemente debido a que
creciendo constantemente debido a que ![]() ; además,
; además, ![]() siendo una infinidad de veces interior a un segmento acotado
siendo una infinidad de veces interior a un segmento acotado ![]() y
y ![]() no rebasando
no rebasando ![]() , tendremos una infinidad de veces
, tendremos una infinidad de veces
 |
|||
![$\displaystyle Y = y\left[ 1 + \sum\frac{A}{(x-a)^2 + y^2} \right]$](img1260.png) |
Vemos que las substituciones de este género son un caso límite de aquellas de segunda especie, los dos puntos dobles atractores siendo iguales a uno situado sobre la circunferencia; los llamaremos entonces substituciones singulares de primera especie. Al contrario de aquellas examinadas anteriormente
![]() deben ser vistas como substituciones singulares de segunda especie.
deben ser vistas como substituciones singulares de segunda especie.
Finalmente, la extensión de los resultados obtenidos en las substituciones de segundo tipo, aquellas que permutan entre si el interior y el exterior de un círculo, es demasiado simple para insistir.
Señalemos que lo que ha sido dicho en el Capítulo I (![]() 6) a propósito de los dominios invariantes encuentra aquí su aplicación, que especialmente el interior y el exterior del círculo fundamental quienes constituyen dos dominios completamente invariantes encierran cada uno la mitad de los puntos críticos de la función inversa.
6) a propósito de los dominios invariantes encuentra aquí su aplicación, que especialmente el interior y el exterior del círculo fundamental quienes constituyen dos dominios completamente invariantes encierran cada uno la mitad de los puntos críticos de la función inversa.
Vamos a mostrar ahora que los métodos utilizados para estudiar las substituciones teniendo un círculo fundamental se aplican a un gran número de casos. Consideremos por ejemplo la substitución (![]() l5):
l5):
Hemos señalado que dicha substitución admite el único punto doble atractor ![]() , siendo el resto de los puntos dobles o periódicos repulsivos. Por otra parte, los
, siendo el resto de los puntos dobles o periódicos repulsivos. Por otra parte, los ![]() convergen uniformemente hacia el infinito en el dominio definido por
convergen uniformemente hacia el infinito en el dominio definido por
![]() este dominio encierra su consecuente y contiene por otra parte los dos puntos críticos de la función inversa
este dominio encierra su consecuente y contiene por otra parte los dos puntos críticos de la función inversa
De lo que resulta que no solamente las longitudes de las curvas ![]() tienden hacia cero, sino que la suma de sus longitudes puede hacerse tan pequeña como se quiera para un valor conveniente de
tienden hacia cero, sino que la suma de sus longitudes puede hacerse tan pequeña como se quiera para un valor conveniente de ![]() . El conjunto perfecto
. El conjunto perfecto ![]() de los puntos que son interiores a una infinidad de curvas
de los puntos que son interiores a una infinidad de curvas ![]() aquí es entonces no solamente discontinuo, sino de longitud nula. Vemos aquí que
aquí es entonces no solamente discontinuo, sino de longitud nula. Vemos aquí que ![]() no está sobre una curva simple, pues contiene dos puntos dobles
no está sobre una curva simple, pues contiene dos puntos dobles ![]()
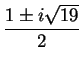 cuyos multiplicadores son imaginarios:
cuyos multiplicadores son imaginarios:
![]() ;
; ![]() siendo perfecto encierra puntos
siendo perfecto encierra puntos ![]() cercanos a
cercanos a ![]() ; si calculamos los antecedentes de
; si calculamos los antecedentes de ![]() por medio de la rama de la función inversa
por medio de la rama de la función inversa ![]() igual a
igual a ![]() para
para ![]() , estos antecedentes tienden a
, estos antecedentes tienden a ![]() agrupandose sobre una curva en espiral teniendo a
agrupandose sobre una curva en espiral teniendo a ![]() por punto asíntoto, de manera que el argumento de
por punto asíntoto, de manera que el argumento de
![]() tuviera más de dos valores límites distintos. Ninguna curva pasando en
tuviera más de dos valores límites distintos. Ninguna curva pasando en ![]() y conteniendo los puntos de
y conteniendo los puntos de ![]() puede entonces tener una tangente única. Transformando la configuración obtenida alrededor de
puede entonces tener una tangente única. Transformando la configuración obtenida alrededor de ![]() , para las substituciones
, para las substituciones ![]() obtenemos configuraciones análogas en torno de los antecedentes de
obtenemos configuraciones análogas en torno de los antecedentes de ![]() que son densos sobre
que son densos sobre ![]() .
.
Obtenemos resultados semejantes sobre numerosos ejemplos de polinomios, por ejemplo de la forma ![]() , si
, si ![]() es suficientemente grande.
es suficientemente grande.
Ahora aquí están ejemplos en los cuales ![]() no es un polinomio. Basta tomar
no es un polinomio. Basta tomar ![]()

![]() . Para
. Para ![]() , tenemos una substitución en el círculo fundamental ya estudiada. No sucede así para
, tenemos una substitución en el círculo fundamental ya estudiada. No sucede así para ![]() . En efecto, tenemos el punto doble atractor
. En efecto, tenemos el punto doble atractor ![]() , y los puntos dobles definidos para
, y los puntos dobles definidos para ![]() , situados sobre la circunferencia
, situados sobre la circunferencia
![]() , y que son repulsores, pues
, y que son repulsores, pues
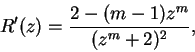
Los consecuentes de un punto ![]() convergen hacia cero para
convergen hacia cero para
![]() y uniformemente en todo círculo de radio
y uniformemente en todo círculo de radio ![]() . Pues, para que
. Pues, para que
![]() sea inferior a
sea inferior a ![]() , basta que
, basta que
![]() sea
sea ![]() , entonces
, entonces
![]() . Para
. Para
![]() , tendremos
, tendremos
![]() . Los puntos críticos de la función
. Los puntos críticos de la función ![]() son por una parte el punto en el infinito, pues para
son por una parte el punto en el infinito, pues para ![]() , la ecuación
, la ecuación

![]() admite una raíz nula y
admite una raíz nula y ![]() raíces infinitas; por otra parte, los puntos que se obtienen haciendo
raíces infinitas; por otra parte, los puntos que se obtienen haciendo
![]() . Tenemos así
. Tenemos así
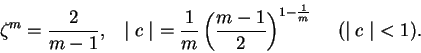
Consideremos un círculo de radio apenas inferior a ![]() conteniendo en su interior los puntos
conteniendo en su interior los puntos ![]() . Sea
. Sea ![]() este círculo; busquemos cual será el dominio antecedente inmediato o todo o al menos la parte de este dominio que es de una sola pieza con el origen y que comprende por consiguiente
este círculo; busquemos cual será el dominio antecedente inmediato o todo o al menos la parte de este dominio que es de una sola pieza con el origen y que comprende por consiguiente ![]() en su interior; la cual comprenderá la parte positiva del eje real, pues cuando
en su interior; la cual comprenderá la parte positiva del eje real, pues cuando ![]() varía de
varía de ![]() a
a ![]() ,
, ![]() varía de
varía de ![]() a
a ![]() pasando por un máximo igual a
pasando por un máximo igual a ![]() para
para
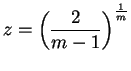 , entonces interior a
, entonces interior a ![]() . Dado lo anterior, consideremos el dominio acotado por la circunferencia
. Dado lo anterior, consideremos el dominio acotado por la circunferencia ![]() de la cual hemos extraído un arco en la vecindad de
de la cual hemos extraído un arco en la vecindad de ![]() ; dos paralelas al eje real de una y otra parte de este eje que trazaremos hasta la circunferencia
; dos paralelas al eje real de una y otra parte de este eje que trazaremos hasta la circunferencia
![]() y que asumiremos suficientemente próximas para que la banda así obtenida a la derecha de
y que asumiremos suficientemente próximas para que la banda así obtenida a la derecha de ![]() tenga su consecuente interior a
tenga su consecuente interior a ![]() , finalmente, la circunferencia
, finalmente, la circunferencia
![]() , suprimiendo el arco comprendido entre las dos paralelas. Tenemos así un contorno simple
, suprimiendo el arco comprendido entre las dos paralelas. Tenemos así un contorno simple ![]() dividiendo el plano en dos regiones simplemente conexas: una región no acotada (que es una parte del antecedente inmediato del interior de
dividiendo el plano en dos regiones simplemente conexas: una región no acotada (que es una parte del antecedente inmediato del interior de ![]() ) comprendiendo los puntos críticos de
) comprendiendo los puntos críticos de ![]() , y teniendo como consecuente inmediato una región que le es completamente interior; por otra parte una región interior a
, y teniendo como consecuente inmediato una región que le es completamente interior; por otra parte una región interior a ![]() donde todas las funciones
donde todas las funciones ![]() son holomorfas. El exterior de
son holomorfas. El exterior de ![]() es un dominio de convergencia uniforme hacia el punto atractor
es un dominio de convergencia uniforme hacia el punto atractor ![]() . Nos encontramos así en las condiciones de la aplicación del parágrafo 21. Decimos que tendremos sobre las curvas
. Nos encontramos así en las condiciones de la aplicación del parágrafo 21. Decimos que tendremos sobre las curvas ![]() a partir de un cierto rango
a partir de un cierto rango
Supongamos que hubieramos tomado el radio del círculo ![]() rigurosamente igual a
rigurosamente igual a ![]() . Si
. Si ![]() está sobre la curva
está sobre la curva
![]() , debemos suponer el argumento de
, debemos suponer el argumento de ![]() comprendido entre
comprendido entre
![]() y
y
![]() (extremos excluidos), si no tendríamos
(extremos excluidos), si no tendríamos
El argumento de
![]() está entonces comprendido entre
está entonces comprendido entre
![]() y
y
![]() y tenemos
y tenemos
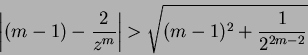
Además
Tenemos entonces
Así entonces las ![]() convergen hacia cero en un dominio que tiene por frontera un conjunto perfecto por todos lados discontinuo. No sabemos si, en el caso actual, la longitud de este conjunto es nula, pero en todos los casos su área es nula, pues la relación de los elementos de área de un dominio limitado por una curva
convergen hacia cero en un dominio que tiene por frontera un conjunto perfecto por todos lados discontinuo. No sabemos si, en el caso actual, la longitud de este conjunto es nula, pero en todos los casos su área es nula, pues la relación de los elementos de área de un dominio limitado por una curva ![]() y de dominio consecuente será inferior a
y de dominio consecuente será inferior a
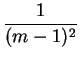 , y como cada
, y como cada ![]() engendra
engendra ![]() , tenemos3.3
, tenemos3.3
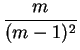
Señalemos rápidamente el ejemplo que sigue:
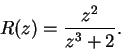
El conjunto frontera del dominio de convergencia es por todas partes discontinuo. Tenemos aquí tres puntos dobles repulsores, de los cuales dos son de multiplicador imaginario.
En resumen, podemos decir que dada una substitución racional
![]() que contiene un punto doble atractor, si podemos encontrar una curva que divida el plano en dos regiones, de las cuales una contiene el punto doble atractor y los puntos críticos de la substitución inversa, y tal que la substitución dada la transforme en otra que le sea completamente interior, de manera que sea parte del dominio de atracción del punto doble, si además, sobre las curvas antecedentes de
que contiene un punto doble atractor, si podemos encontrar una curva que divida el plano en dos regiones, de las cuales una contiene el punto doble atractor y los puntos críticos de la substitución inversa, y tal que la substitución dada la transforme en otra que le sea completamente interior, de manera que sea parte del dominio de atracción del punto doble, si además, sobre las curvas antecedentes de ![]() , tenemos a partir de cierto rango
, tenemos a partir de cierto rango
Veremos en el capítulo siguiente que ciertas condiciones enunciadas aquí son redundantes.
No es inútil hacer a propósito de este teorema algunas observaciones complementarias. Primero tener interés en tener para las curvas antecedentes del parágrafo 21 un sistema de numeración que no sea arbitrario. Si designamos por
![]() las determinaciones de la función inversa, uniformes y distintas en el interior de
las determinaciones de la función inversa, uniformes y distintas en el interior de ![]() , es natural designar por el grupo de cifras
, es natural designar por el grupo de cifras
![]() la curva
la curva ![]() que se deriva de
que se deriva de ![]() por la substitución
por la substitución
![]() ; de esta manera vemos enseguida que:
; de esta manera vemos enseguida que: ![]() para que dos curvas
para que dos curvas ![]() y
y
![]() sean interiores una en otra, es necesario y suficiente que el grupo de cifras o índice de
sean interiores una en otra, es necesario y suficiente que el grupo de cifras o índice de ![]() comienze por las cifras de
comienze por las cifras de ![]() ;
; ![]() que los índices de los consecuentes de
que los índices de los consecuentes de ![]() se obtienen suprimiendo sucesivamente
se obtienen suprimiendo sucesivamente
![]() cifras a la izquierda de su índice;
cifras a la izquierda de su índice; ![]() que los antecedentes de
que los antecedentes de ![]() se obtienen agregando cifras a la izquierda del índice. Enseguida infinidad de cifras harán corresponder el punto interior común a todas las curvas teniendo por índices sucesivos los grupos de
se obtienen agregando cifras a la izquierda del índice. Enseguida infinidad de cifras harán corresponder el punto interior común a todas las curvas teniendo por índices sucesivos los grupos de
![]() primeras cifras de la serie; de esta manera, hay correspondencia biunívoca entre los puntos de
primeras cifras de la serie; de esta manera, hay correspondencia biunívoca entre los puntos de ![]() y las series infinitas de cifras en cuestión. A esta serie de cifras corresponde además el número comprendido entre
y las series infinitas de cifras en cuestión. A esta serie de cifras corresponde además el número comprendido entre ![]() y
y ![]() , tal que la serie de estas cifras representativas después de la coma en el sistema de numeración en base
, tal que la serie de estas cifras representativas después de la coma en el sistema de numeración en base ![]() sea la serie propuesta, siendo biunívoca la correspondencia, excepto para una infinidad de número racionales que pueden escribirse de dos maneras, a saber aquellos que pueden escribirse de manera que no tengan ceros a partir de un cierto rango y que también podemos escribir no empleando más que la cifra
sea la serie propuesta, siendo biunívoca la correspondencia, excepto para una infinidad de número racionales que pueden escribirse de dos maneras, a saber aquellos que pueden escribirse de manera que no tengan ceros a partir de un cierto rango y que también podemos escribir no empleando más que la cifra ![]() a partir de un cierto rango.
a partir de un cierto rango.
Vemos así que ![]() tiene la potencia del continuo; no hemos hecho mas que repetir, en un caso particular, la demostración clásica de esta propiedad de los conjuntos perfectos, pero aquí el modo de representación adoptado para
tiene la potencia del continuo; no hemos hecho mas que repetir, en un caso particular, la demostración clásica de esta propiedad de los conjuntos perfectos, pero aquí el modo de representación adoptado para ![]() está en relación estrecha con las propiedades de invarianza de este conjunto con relación a la substitución dada. En particular, a las fracciones periódicas simples les corresponden los puntos periódicos, a las fracciones periódicas mixtas los antecedentes de estos puntos. Si dejamos de lado los desarrollos que se terminan por cero repetido indefinidamente, tenemos una correspondencia biunívoca entre los números reales
está en relación estrecha con las propiedades de invarianza de este conjunto con relación a la substitución dada. En particular, a las fracciones periódicas simples les corresponden los puntos periódicos, a las fracciones periódicas mixtas los antecedentes de estos puntos. Si dejamos de lado los desarrollos que se terminan por cero repetido indefinidamente, tenemos una correspondencia biunívoca entre los números reales
![]() por una parte y los puntos de
por una parte y los puntos de ![]() por la otra, con la exclusión de los antecedentes de uno de los puntos dobles que no son representados. A dos puntos de
por la otra, con la exclusión de los antecedentes de uno de los puntos dobles que no son representados. A dos puntos de ![]() infinitamente cercanos corresponden dos valores de
infinitamente cercanos corresponden dos valores de ![]() infinitamente cercanos; la recíproca no es válida, la cantidad compleja que corresponde a un punto de
infinitamente cercanos; la recíproca no es válida, la cantidad compleja que corresponde a un punto de ![]() siendo una función discontinua de
siendo una función discontinua de ![]() para los valores de
para los valores de ![]() en representación ambigua, pero continua por todas partes. Si establecemos
en representación ambigua, pero continua por todas partes. Si establecemos ![]() conviniendo que
conviniendo que
![]() , tenemos
, tenemos ![]() . Con la ayuda de estas observaciones, demostramos inmediatamente:
. Con la ayuda de estas observaciones, demostramos inmediatamente: ![]() que todo punto de
que todo punto de ![]() es límite de puntos periódicos;
es límite de puntos periódicos; ![]() que hay, en la vecindad de cada punto de
que hay, en la vecindad de cada punto de ![]() , puntos tales que el conjunto derivado de sus consecuentes sea idéntico a
, puntos tales que el conjunto derivado de sus consecuentes sea idéntico a ![]() , etc. ( cf.
, etc. ( cf. ![]() 20 ).
20 ).
Otra observación que tiene lugar, es que la existencia de un dominio de convergencia en la frontera por todas partes discontinua no es un caso singular, es decir que esta circunstancia se producirá sin que haya des-i-gual-da-des particulares entre los coeficientes de la función ![]() ; basta que estos coeficientes varien en un dominio conveniente. Consideremos una substitución racional de grado
; basta que estos coeficientes varien en un dominio conveniente. Consideremos una substitución racional de grado ![]() para la cual el hecho se produce, por ejemplo una substitución en el círculo fundamental de la segunda especie no singular y sea una curva
para la cual el hecho se produce, por ejemplo una substitución en el círculo fundamental de la segunda especie no singular y sea una curva ![]() que divide el plano en dos regiones gozando de las propiedades indicadas con anterioridad, el exterior de
que divide el plano en dos regiones gozando de las propiedades indicadas con anterioridad, el exterior de ![]() conteniendo los puntos críticos de
conteniendo los puntos críticos de ![]() y el punto doble atractor. Si hacemos variar los coeficientes de
y el punto doble atractor. Si hacemos variar los coeficientes de ![]() , los
, los ![]() puntos críticos de
puntos críticos de ![]() , que se obtienen igualando a cero el discriminante de la ecuación
, que se obtienen igualando a cero el discriminante de la ecuación ![]() , variarán de una manera continua y permanecerán exteriores a
, variarán de una manera continua y permanecerán exteriores a ![]() para una variación suficientemente pequeña de los coeficientes. Como por otra parte
para una variación suficientemente pequeña de los coeficientes. Como por otra parte ![]() es una función uniformemente continua de
es una función uniformemente continua de ![]() y de los coeficientes en el dominio
y de los coeficientes en el dominio ![]() exterior a
exterior a ![]() , la propiedad consistiendo, en que
, la propiedad consistiendo, en que
![]() es interior a
es interior a ![]() subsistirá igualmente; por una razón análoga, aún tendremos
subsistirá igualmente; por una razón análoga, aún tendremos
![]() sobre
sobre ![]() y en su interior
y en su interior ![]() . Decimos que, en
. Decimos que, en ![]() las
las ![]() convergerán hacia un punto doble atractor. En efecto, tal punto doble existe aún en
convergerán hacia un punto doble atractor. En efecto, tal punto doble existe aún en ![]() , ya que las raíces de la ecuación
, ya que las raíces de la ecuación ![]() y los multiplicadores correspondientes
y los multiplicadores correspondientes ![]() son funciones continuas de los coeficientes; sean
son funciones continuas de los coeficientes; sean ![]() el punto doble y
el punto doble y ![]() un punto interior a
un punto interior a ![]() . Las funciones
. Las funciones
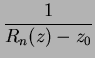 siendo acotadas en su conjunto en
siendo acotadas en su conjunto en ![]() y tendiendo uniformemente hacia
y tendiendo uniformemente hacia
 en un pequeño círculo de centro
en un pequeño círculo de centro ![]() interior a
interior a ![]() tenderán uniformemente hacia esta constante en todo el dominio
tenderán uniformemente hacia esta constante en todo el dominio ![]() 3.4. Entonces los
3.4. Entonces los ![]() convergen hacia
convergen hacia ![]() en
en ![]() y finalmente en el dominio teniendo por frontera el conjunto discontinuo
y finalmente en el dominio teniendo por frontera el conjunto discontinuo ![]() .
.
Podemos precisar más cuando ![]() es un polinomio: basta que el término constante de
es un polinomio: basta que el término constante de ![]() sea suficientemente grande, el resto de los coeficientes siendo dados para que la substitución
sea suficientemente grande, el resto de los coeficientes siendo dados para que la substitución
![]() entre en la categoría anterior. Establezcamos
entre en la categoría anterior. Establezcamos
siendo ![]() un parámetro. La desigualdad
un parámetro. La desigualdad
![]() define uno o más dominios acotados
define uno o más dominios acotados ![]() , que son fijos cuando
, que son fijos cuando ![]() varía. Sea
varía. Sea ![]() el máximo3.5 de las distancias de estos dominios al origen. Tomamos siempre
el máximo3.5 de las distancias de estos dominios al origen. Tomamos siempre
![]() . Siendo lo anterior, para que tuvieramos
. Siendo lo anterior, para que tuvieramos
![]() , basta que
, basta que ![]() sea superior a la raíz positiva de la ecuación
sea superior a la raíz positiva de la ecuación
Para que ![]() estuviera en un dominio tal como
estuviera en un dominio tal como ![]() , basta que
, basta que
![]() , es decir, con
, es decir, con
![]() estableciendo que
estableciendo que
El coeficiente de ![]() siendo positivo en el primer número, lo que tendrá lugar cuando
siendo positivo en el primer número, lo que tendrá lugar cuando ![]() sea superior a
sea superior a ![]() siendo, por ejemplo, la raíz positiva más grande del primer número.
siendo, por ejemplo, la raíz positiva más grande del primer número.
Tomaremos entonces
![]() , y
, y ![]() suficientemente cercano a
suficientemente cercano a ![]() para que la desigualdad
para que la desigualdad
![]() conlleve a
conlleve a
![]() , lo cual es posible en virtud del análisis anterior;
, lo cual es posible en virtud del análisis anterior; ![]() contiene entonces los consecuentes de los dominios
contiene entonces los consecuentes de los dominios ![]() y en particular los consecuentes inmediatos de los puntos raíz de
y en particular los consecuentes inmediatos de los puntos raíz de ![]() que junto con el punto al infinito constituyen los puntos críticos de
que junto con el punto al infinito constituyen los puntos críticos de ![]() . Además, sobre las curvas antecedentes del contorno
. Además, sobre las curvas antecedentes del contorno ![]() de
de ![]() , tenemos
, tenemos
![]() , a partir del primer rango. Estamos entonces en el caso donde la frontera del dominio de convergencia hacia el infinito es en todas partes discontinuo (y de longitud nula si
, a partir del primer rango. Estamos entonces en el caso donde la frontera del dominio de convergencia hacia el infinito es en todas partes discontinuo (y de longitud nula si ![]() ).
).
Ahora vamos a estudiar ejemplos de substituciones racionales con dos puntos dobles atractores, cuyos dominios respectivos son simplemente conexos de una sola pieza, y separados por una curva como en las substituciones en el círculo fundamental de primera especie.
Tomemos, por ejemplo ![]()
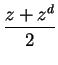
![]() . Aquí tenemos dos puntos dobles atractores, el punto en el infinito y el origen. Constatamos fácilmente que el dominio del punto en el infinito comprende el exterior de todo círculo
. Aquí tenemos dos puntos dobles atractores, el punto en el infinito y el origen. Constatamos fácilmente que el dominio del punto en el infinito comprende el exterior de todo círculo ![]() de radio superior a
de radio superior a
![]() y que en un dominio como éste tenemos:
y que en un dominio como éste tenemos:
![]() . De igual manera, el dominio del origen comprende el interior de todo círculo
. De igual manera, el dominio del origen comprende el interior de todo círculo ![]() de radio más pequeño que
de radio más pequeño que ![]() , en el cual tendremos:
, en el cual tendremos:
![]() . Los puntos críticos de
. Los puntos críticos de ![]() son el punto en el infinito en torno al cual se permutan circularmente las
son el punto en el infinito en torno al cual se permutan circularmente las ![]() ramas de
ramas de ![]() y los puntos
y los puntos ![]() ,
, ![]()
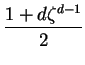
![]() , lo que da
, lo que da ![]() puntos críticos simples, todos interiores a
puntos críticos simples, todos interiores a ![]() , si tomamos el radio de
, si tomamos el radio de ![]() superior a
superior a
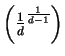 .
.
Los valores de ![]() se permutan circularmente sobre las circunferencias
se permutan circularmente sobre las circunferencias ![]() y
y ![]() . De lo que podemos deducir fácilmente que las curvas antecedentes de
. De lo que podemos deducir fácilmente que las curvas antecedentes de ![]() son curvas simples de una sola pieza
son curvas simples de una sola pieza
![]() tales que
tales que ![]() sea interior a
sea interior a ![]() y comprendiendo todas el origen en su interior, de manera que
y comprendiendo todas el origen en su interior, de manera que ![]() regrese a su punto de partida sobre
regrese a su punto de partida sobre ![]() , habiendo aumentado su argumento en
, habiendo aumentado su argumento en ![]() cuando
cuando ![]() a hecho
a hecho ![]() veces el contorno de
veces el contorno de ![]() en el sentido directo.
en el sentido directo.
De igual forma, las curvas antecedentes de ![]() son curvas que se desarrollan, mutuamente comprendiendo siempre el origen en su interior y permaneciendo exteriores a las curvas
son curvas que se desarrollan, mutuamente comprendiendo siempre el origen en su interior y permaneciendo exteriores a las curvas ![]() . Los dominios antecedentes del interior de
. Los dominios antecedentes del interior de ![]() y del exterior de
y del exterior de ![]() son así dominios simplemente conexos cada vez más grandes, limitados por las curvas
son así dominios simplemente conexos cada vez más grandes, limitados por las curvas ![]() y
y ![]() ; vamos a ver en un momento que la distancia entre las curvas
; vamos a ver en un momento que la distancia entre las curvas ![]() y
y ![]() tiende uniformemente a cero.
tiende uniformemente a cero.
Para precisar la manera en la cual las cosas suceden, tracemos en la corona ![]() , donde las funciones
, donde las funciones ![]() son analíticas pero no uniformes, el corte
son analíticas pero no uniformes, el corte ![]() orientado según el segmento del eje real positivo;
orientado según el segmento del eje real positivo; ![]() contiene entonces el punto doble repulsor
contiene entonces el punto doble repulsor ![]() , y la rama de
, y la rama de ![]() , que es igual a
, que es igual a ![]() para
para ![]() , permanece real para
, permanece real para ![]() situado sobre
situado sobre ![]() , de manera que los segmentos antecedentes de
, de manera que los segmentos antecedentes de ![]() obtenidos a través de esta función, son encajados unos en otros y tienden hacia el punto doble
obtenidos a través de esta función, son encajados unos en otros y tienden hacia el punto doble ![]() . Designaremos por
. Designaremos por
![]() las ramas
las ramas ![]() de la función
de la función ![]() obtenidas sucesivamente partiendo de un punto del corte con la determinación inicial igualmente situada sobre el corte, y regresando en torno al origen en el sentido directo. En el dominio inicial
obtenidas sucesivamente partiendo de un punto del corte con la determinación inicial igualmente situada sobre el corte, y regresando en torno al origen en el sentido directo. En el dominio inicial ![]() , constituido por la corona donde trazamos el corte, corresponden así
, constituido por la corona donde trazamos el corte, corresponden así ![]() dominios
dominios ![]() que asignaremos como índices superiores
que asignaremos como índices superiores
![]() y que están constituidos por cuadriláteros curvilíneos reunidos en la corona comprendida entre
y que están constituidos por cuadriláteros curvilíneos reunidos en la corona comprendida entre ![]() y
y ![]() , sin que dichos dominios tengan puntos interiores en común, aunque dos dominios de índices
, sin que dichos dominios tengan puntos interiores en común, aunque dos dominios de índices ![]() y
y ![]() (ó
(ó ![]() y
y ![]() ) sean continuos siguiendo una línea transversal antecedente del corte
) sean continuos siguiendo una línea transversal antecedente del corte ![]() . Los dominios antecedentes inmediatos de las
. Los dominios antecedentes inmediatos de las ![]() , es decir los dominios
, es decir los dominios ![]() , serán obtenidos a través de la aplicación de
, serán obtenidos a través de la aplicación de ![]() junto con los dominios
junto con los dominios ![]() , que están contenidos en el orden en que los encontramos, sucesivamente sobre
, que están contenidos en el orden en que los encontramos, sucesivamente sobre
![]() . Estos dominios
. Estos dominios ![]() reunidos en la corona
reunidos en la corona
![]() tendrán por índices sucesivos en el orden en que los encontramos
tendrán por índices sucesivos en el orden en que los encontramos
Vemos además claramente como los dominios ![]() son reunidos, considerando, en lugar del ejemplo estudiado, lo siguiente,
son reunidos, considerando, en lugar del ejemplo estudiado, lo siguiente, ![]() , que da
, que da
Los dominios ![]() son entonces limitados por las circunferencias concéntricas y los segmentos de radios angularmente equidistantes; pero desde el punto de vista del Analysis situs, todo sucede como en el presente ejemplo.
son entonces limitados por las circunferencias concéntricas y los segmentos de radios angularmente equidistantes; pero desde el punto de vista del Analysis situs, todo sucede como en el presente ejemplo.
Estudiemos ahora el conjunto límite de los dominios ![]() , es decir el conjunto de los puntos interiores en sentido amplio a una infinidad de estos dominios. Decimos que, las dimensiones de estos dominios tienden uniformemente a cero con
, es decir el conjunto de los puntos interiores en sentido amplio a una infinidad de estos dominios. Decimos que, las dimensiones de estos dominios tienden uniformemente a cero con
![]() . En efecto, basta demostrar, según un razonamiento ya empleado, que tenemos
. En efecto, basta demostrar, según un razonamiento ya empleado, que tenemos
Los cálculos elementales que omitimos muestran que ésto aún se cumple para ![]() ó
ó ![]() . Las longitudes de los contornos de los dominios
. Las longitudes de los contornos de los dominios ![]() tienden así uniformemente hacia cero con
tienden así uniformemente hacia cero con
![]() ; de lo que se sigue que el conjunto límite de los puntos de la corona
; de lo que se sigue que el conjunto límite de los puntos de la corona
![]() es un conjunto perfecto, bien conectado, sin puntos interiores. A toda serie infinita de enteros
es un conjunto perfecto, bien conectado, sin puntos interiores. A toda serie infinita de enteros
![]() podemos hacer corresponder el punto de este conjunto
podemos hacer corresponder el punto de este conjunto ![]() que es interior en sentido amplio a los dominios teniendo por índices
que es interior en sentido amplio a los dominios teniendo por índices
![]() , que son interiores en sentido amplio unos a otros. A dos series de enteros distintas corresponderán en general dos puntos distintos, lo contrario tiene lugar sólo si estas dos series representan el mismo número comprendido entre
, que son interiores en sentido amplio unos a otros. A dos series de enteros distintas corresponderán en general dos puntos distintos, lo contrario tiene lugar sólo si estas dos series representan el mismo número comprendido entre ![]() y
y ![]() en el sistema de numeración en base
en el sistema de numeración en base ![]() . En efecto, resulta de aquello que a sido dicho anteriormente que el orden de sucesión de los dominios
. En efecto, resulta de aquello que a sido dicho anteriormente que el orden de sucesión de los dominios ![]() es el mismo que el orden natural de los números
es el mismo que el orden natural de los números
A dos valores de ![]() infinitamente cercanos corresponderán dos puntos infinitamente cercanos, estos dos puntos perteneciendo a un mismo dominio
infinitamente cercanos corresponderán dos puntos infinitamente cercanos, estos dos puntos perteneciendo a un mismo dominio ![]() para un valor infinitamente grande de
para un valor infinitamente grande de ![]() , y las dimensiones de
, y las dimensiones de ![]() tienden hacia cero con
tienden hacia cero con
![]() .
.
Así, hay correspondencia continua y biunívoca entre los puntos del conjunto ![]() y los números comprendidos entre
y los números comprendidos entre ![]() y
y ![]() . Los puntos de
. Los puntos de ![]() forman una curva representada por una ecuación de la forma
forman una curva representada por una ecuación de la forma
Vemos en definitiva que, gracias a la introducción de un corte invariante pasando por un punto doble repulsor, hemos podido hacer el estudio de la frontera de los dominios de atracción de los dos puntos dobles ( ![]() e
e ![]() ) de la misma manera que en el caso recien examinado donde la frontera es discontinua.
) de la misma manera que en el caso recien examinado donde la frontera es discontinua.
En el presente caso, tenemos una separación del plano en dos regiones simplemente conexas por una línea continua; son las regiones de convergencia respectivas a los dos puntos dobles; vemos fácilmente que todo punto de la línea frontera es límite de los antecedentes de un punto cualquiera del plano, excepto el punto al infinito. Mas precisamente, el consecuente de orden ![]() de un dominio circular tan pequeño como queramos teniendo por centro un punto de la frontera cubre todo el plano, salvo el exterior de un círculo de radio arbitario, para un valor finito de
de un dominio circular tan pequeño como queramos teniendo por centro un punto de la frontera cubre todo el plano, salvo el exterior de un círculo de radio arbitario, para un valor finito de ![]() .
.
El ejemplo anterior puede ser fácilmente generalizado. Supongamos que dos puntos dobles atractores de una substitución racional (siempre podemos suponer el origen y el infinito) pueden ser respectivamente rodeados de dos contornos simples sin puntos dobles ![]() y
y ![]() gozando de las propiedades siguientes: los consecuentes de un punto de
gozando de las propiedades siguientes: los consecuentes de un punto de ![]() o interior a
o interior a ![]() son interiores a
son interiores a ![]() , los consecuentes de un punto de
, los consecuentes de un punto de ![]() o exterior a
o exterior a ![]() son exteriores a
son exteriores a ![]() ; sobre
; sobre ![]() y
y ![]() , todas las determinaciones de
, todas las determinaciones de ![]() se permutan circularmente. Existe entonces (Chap. I,
se permutan circularmente. Existe entonces (Chap. I, ![]() 6)
6) ![]() puntos críticos de
puntos críticos de ![]() en el interior de
en el interior de ![]() así como en el exterior de
así como en el exterior de ![]() , entonces no hay puntos en la corona
, entonces no hay puntos en la corona ![]() . Los antecedentes de
. Los antecedentes de ![]() y
y ![]() son curvas simples de una sola pieza, las coronas
son curvas simples de una sola pieza, las coronas
![]() son interiores a aquellas de rango menor; supondremos que tenemos en estas coronas, a partir de un cierto rango,
son interiores a aquellas de rango menor; supondremos que tenemos en estas coronas, a partir de un cierto rango,
Siendo la serie
![]() absolutamente convergente, tenemos
absolutamente convergente, tenemos

Además, las longitudes de las curvas ![]() tendiendo hacia cero por la misma razón que
tendiendo hacia cero por la misma razón que
![]() , los puntos
, los puntos ![]() tienden hacia el mismo punto doble
tienden hacia el mismo punto doble ![]() . Las líneas
. Las líneas
![]() constituyen por su reunión un corte de la corona
constituyen por su reunión un corte de la corona ![]() invariante por la substitución dada, teniendo un segmento único en las coronas
invariante por la substitución dada, teniendo un segmento único en las coronas ![]()
![]() , de longitud finita y sin punto doble, que tendrá en
, de longitud finita y sin punto doble, que tendrá en ![]() un punto asíntoto si
un punto asíntoto si ![]() es imaginario, pero jugando en todos los casos el mismo rol que el corte rectilíneo del ejemplo anterior. Los dominios de los dos puntos dobles atractores
es imaginario, pero jugando en todos los casos el mismo rol que el corte rectilíneo del ejemplo anterior. Los dominios de los dos puntos dobles atractores ![]() y
y ![]() aún son dominios simplemente conexos separados por una curva sin punto doble
aún son dominios simplemente conexos separados por una curva sin punto doble
Aún señalaremos que el caso examinado aquí no es un caso singular, las mismas circunstancias se presentan si damos incrementos suficientemente pequeños, a los coeficientes de ![]() .
.
Dejaremos de lado por el momento los casos, límites de los anteriores, donde hay un punto doble de multiplicador igual a ![]() , y vamos a estudiar substituciones cuya iteración conduce a considerar dominios de un caracter diferente a aquellos examinados hasta el momento. Estos nuevos ejemplos se deducen del resto fácilmente de las substituciones en el círculo fundamental por una transformación algebraica de segundo orden.
, y vamos a estudiar substituciones cuya iteración conduce a considerar dominios de un caracter diferente a aquellos examinados hasta el momento. Estos nuevos ejemplos se deducen del resto fácilmente de las substituciones en el círculo fundamental por una transformación algebraica de segundo orden.
Nos proponemos el problema siguiente: encontrar una substitución racional para la cual existe un conjunto de puntos completamente invariantes formado por un arco de círculo; este arco debe entonces contener los consecuentes y antecedentes de todos sus puntos. Podemos, por medio de una transformación homográfica previa, reemplazar este arco por el semi-eje real positivo. Sea ![]() la substitución buscada;
la substitución buscada; ![]() y
y ![]() toman simultáneamente valores reales positivos o nulos.
toman simultáneamente valores reales positivos o nulos.
Establezcamos
![]() será real para
será real para ![]() real positivo; si
real positivo; si ![]() no está sobre
no está sobre ![]() ,
, ![]() estará, por ejemplo, en el semi-plano superior;
estará, por ejemplo, en el semi-plano superior; ![]() o
o ![]() siendo igualmente exterior a
siendo igualmente exterior a ![]() ,
, ![]() estará afuera del eje real; tomamos
estará afuera del eje real; tomamos ![]() en el semi-plano superior como
en el semi-plano superior como ![]() . Si
. Si ![]() varía permaneciendo en el semi-plano superior, igual sucederá para
varía permaneciendo en el semi-plano superior, igual sucederá para ![]() , estos dos puntos llegando al mismo tiempo al eje real. De lo que se sigue que la función
, estos dos puntos llegando al mismo tiempo al eje real. De lo que se sigue que la función ![]() así definida es racional. Tenemos, en efecto,
así definida es racional. Tenemos, en efecto,
![]() y los puntos críticos de esta función de
y los puntos críticos de esta función de ![]() son los ceros y los polos de
son los ceros y los polos de ![]() .
. ![]() llega a ser nula o infinito para
llega a ser nula o infinito para ![]() ,
, ![]() siendo real. Si
siendo real. Si ![]() es finita y diferente de cero y si
es finita y diferente de cero y si ![]() es una raíz de orden impar de
es una raíz de orden impar de ![]() , tendremos
, tendremos
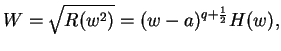 |
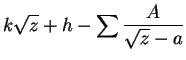 |
|||
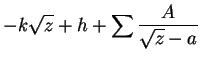 |
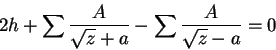
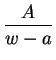 y
y
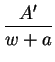 proporcionan entonces en la expresión anterior una contribución igual a
proporcionan entonces en la expresión anterior una contribución igual a
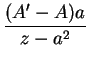 . Si
. Si
De lo que deducimos
![\begin{displaymath}
Z = z\left[ k - \sum\frac{2A}{z - a^2}, \right]^2 = R(z).
\end{displaymath}](img1494.png)
Tal es la expresión general de las substituciones que satisfacen a las condiciones del problema.
Si damos a ![]() tal que no esté situada sobre la parte positiva del eje real, le corresponden dos valores de
tal que no esté situada sobre la parte positiva del eje real, le corresponden dos valores de
![]() , fuera del eje real; sean
, fuera del eje real; sean ![]() uno de ellos,
uno de ellos,
![]() ; los puntos
; los puntos ![]() permanecen del mismo lado del eje real y tienden hacia el punto límite
permanecen del mismo lado del eje real y tienden hacia el punto límite ![]() situado sobre el eje real, o bien fuera, según la especie de la substitución
situado sobre el eje real, o bien fuera, según la especie de la substitución ![]() . Los puntos
. Los puntos ![]() , que se deducen de
, que se deducen de ![]() por iteración de la substitución
por iteración de la substitución ![]() , tienen entonces por límite al punto
, tienen entonces por límite al punto ![]() , vemos fácilmente que
, vemos fácilmente que ![]() siempre es real.
siempre es real.
Si ![]() es de la segunda especie, con un punto atractor único sobre el eje real, hay sobre este eje una infinidad numerable de segmentos contiguos en un conjunto perfecto
es de la segunda especie, con un punto atractor único sobre el eje real, hay sobre este eje una infinidad numerable de segmentos contiguos en un conjunto perfecto ![]() en el interior de los cuales las
en el interior de los cuales las ![]() convergen hacia
convergen hacia ![]() . Le corresponde una infinidad numerable de segmentos situados sobre
. Le corresponde una infinidad numerable de segmentos situados sobre ![]() , contiguos a un conjunto perfecto
, contiguos a un conjunto perfecto ![]() sobre los cuales las
sobre los cuales las ![]() convergen hacia
convergen hacia ![]() .
. ![]() es por todas partes discontinuo; los consecuentes de un segmento que contienen un punto de
es por todas partes discontinuo; los consecuentes de un segmento que contienen un punto de ![]() terminan por recubrir completamente
terminan por recubrir completamente ![]() . Nada hay en este caso esencialmente nuevo. Al contrario, si
. Nada hay en este caso esencialmente nuevo. Al contrario, si ![]() es de la primera especie hay convergencia para todo el plano hacia el punto
es de la primera especie hay convergencia para todo el plano hacia el punto ![]() (
( ![]() siendo un imaginario puro), salvo sobre la parte positiva del eje real que forma la frontera continua del dominio de convergencia. Tenemos entonces un dominio de convergencia de alguna otra naturaleza a la de los encontrados hasta aquí. Encontraremos fácilmente las condiciones que deben satisfacer las constantes
siendo un imaginario puro), salvo sobre la parte positiva del eje real que forma la frontera continua del dominio de convergencia. Tenemos entonces un dominio de convergencia de alguna otra naturaleza a la de los encontrados hasta aquí. Encontraremos fácilmente las condiciones que deben satisfacer las constantes ![]() para que ésto sea así. Si por ejemplo suponemos todas las
para que ésto sea así. Si por ejemplo suponemos todas las ![]() diferentes de cero, estas condiciones son
diferentes de cero, estas condiciones son
Dejaremos de lado la discusión de la posición de los puntos dobles que no presentan dificultades.
Si ahora efectuamos sobre ![]() y
y ![]() una misma transformación homográfica cualquiera, obtenemos la expresión general de las substituciones que dejan invariante un arco de círculo
una misma transformación homográfica cualquiera, obtenemos la expresión general de las substituciones que dejan invariante un arco de círculo ![]() y el dominio no acotado que tiene a este arco por frontera;
si existe un punto doble exterior a
y el dominio no acotado que tiene a este arco por frontera;
si existe un punto doble exterior a ![]() , éste es entonces un punto doble atractor sobre la prolongación de
, éste es entonces un punto doble atractor sobre la prolongación de ![]() y cuyo dominio comprende todo el plano a excepción del corte
y cuyo dominio comprende todo el plano a excepción del corte ![]() . En todos los casos, demostramos fácilmente que la substitución inversa
. En todos los casos, demostramos fácilmente que la substitución inversa ![]() admite
admite ![]() puntos críticos exteriores a
puntos críticos exteriores a ![]() , los
, los ![]() valores de esta función se permutan circularmente sobre un contorno rodeando
valores de esta función se permutan circularmente sobre un contorno rodeando ![]() y cercano a este arco; igualmente hay puntos críticos sobre
y cercano a este arco; igualmente hay puntos críticos sobre ![]() equivalentes a
equivalentes a ![]() puntos críticos simples y que son todos iguales a los puntos
puntos críticos simples y que son todos iguales a los puntos ![]() y
y ![]() (excepcionalmente a uno solo de estos puntos, si
(excepcionalmente a uno solo de estos puntos, si ![]() es de segundo grado). Describiendo
es de segundo grado). Describiendo ![]() el arco
el arco ![]() ,
, ![]() describe
describe ![]() veces este mismo arco en el mismo sentido mientras no alcanze los extremos
veces este mismo arco en el mismo sentido mientras no alcanze los extremos ![]() y
y ![]() . Tenemos, entre
. Tenemos, entre ![]() y
y ![]() , uno de los cuatro sistemas de relaciones:
, uno de los cuatro sistemas de relaciones:
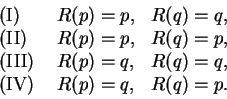
Todo lo cual es muy fácil de verificar mismo que resulta de que ![]() no puede tener puntos críticos interiores a
no puede tener puntos críticos interiores a ![]() .
.
Como ejemplo, busquemos si existen polinomios dejando invariante el segmento ![]() del eje real y el dominio exterior a este segmento. Sea
del eje real y el dominio exterior a este segmento. Sea ![]() un polinomio respondiendo a la cuestión. Si establecemos
un polinomio respondiendo a la cuestión. Si establecemos
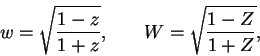
Si establecemos
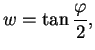 |
|||
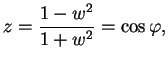 |
Somos llevados a buscar la condición para que
![]() sea una función racional de
sea una función racional de ![]() . Basta que
. Basta que ![]() sea un múltiplo de
sea un múltiplo de ![]() . Los polinomios buscados son entonces aquellos que expresan
. Los polinomios buscados son entonces aquellos que expresan ![]() en funcion de
en funcion de
![]() . Tenemos así una representación paramétrica cómoda que pone en evidencia las propiedades de las subtituciones iteradas.
. Tenemos así una representación paramétrica cómoda que pone en evidencia las propiedades de las subtituciones iteradas.
Finalmente señalamos que es posible formar ejemplos análogos de substituciones que tienen un punto doble atractor con un dominio cuya frontera está constituida por una curva de Jordan no cerrada, esta curvatura no siendo un arco del círculo sino una curva no analítica. A la inversa de los casos tratados al inicio de este Capítulo, este caso es singular, es decir suponemos siempre satisfechas ciertas relaciones entre los coeficientes de la substitución. Regresaremos posteriormente sobre este sujeto.
FIN DEL TOMO XLVII.