Debemos recordar, antes de otra cosa, los resultados relativos a los puntos dobles de multiplicador inferior, en módulo, a la unidad a los que llamaremos
puntos dobles atractores; regresando, para más detalle, a las investigaciones ya citadas de M. K![]() nings. Sea
nings. Sea ![]() un punto doble atractor en la vecindad del cual
un punto doble atractor en la vecindad del cual ![]() puede desarrollarse en serie de Taylor:
puede desarrollarse en serie de Taylor:
Existe un número ![]() y un número
y un número ![]() comprendido entre
comprendido entre ![]() y
y ![]() tal que de la desigualdad
tal que de la desigualdad
![]() se deriva
se deriva
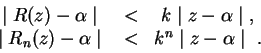
De lo cual se obtiene que, estando ![]() en el cículo
en el cículo ![]() de radio
de radio ![]() y de centro
y de centro ![]() , su
, su ![]() -ésimo consecuente tiende uniformemente hacia
-ésimo consecuente tiende uniformemente hacia ![]() para
para ![]() infinito. Además, si
infinito. Además, si ![]() , la relación
, la relación
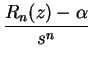 tiende uniformemente hacia una función
tiende uniformemente hacia una función
![]() holomorfa en
holomorfa en ![]() y satisfaciendo la ecuación funcional de Schröder
y satisfaciendo la ecuación funcional de Schröder
con las condiciones ![]() ,
,
![]() . El cambio de variable
. El cambio de variable
![]() que equivale a la representación conforme y biunivoca en la
vecindad de
que equivale a la representación conforme y biunivoca en la
vecindad de ![]() , permite llevar la sustitución
, permite llevar la sustitución ![]() a la
forma canónica
a la
forma canónica ![]() . De lo anterior deducimos
. De lo anterior deducimos
Del grupo de substituciones lineales
![]() , siendo estrictamente discontinuo en todo dominio limitado que no encierra el punto
, siendo estrictamente discontinuo en todo dominio limitado que no encierra el punto ![]() ,
deduciremos que el grupo
,
deduciremos que el grupo ![]() no es estrictamente discontinuo en toda corona comprendida entre dos círculos de radio suficientemente pequeño.
Lo mismo sucede en todos lo dominios antecedentes de este dominio coronal.
no es estrictamente discontinuo en toda corona comprendida entre dos círculos de radio suficientemente pequeño.
Lo mismo sucede en todos lo dominios antecedentes de este dominio coronal.
Consideremos ahora el caso de un punto doble de multiplicador nulo. Podemos, por una transformación lineal simple, regresar la substitución a la forma
con el punto doble en el origen. Consideremos entonces un círculo ![]() con centro en el origen y de radio suficientemente pequeño para contener en su interior los consecuentes de todos los puntos y para que, por otra parte,
la funcion
con centro en el origen y de radio suficientemente pequeño para contener en su interior los consecuentes de todos los puntos y para que, por otra parte,
la funcion ![]() no posea más que un solo cero en el origen. Las funciones
no posea más que un solo cero en el origen. Las funciones
![]() son entonces, holomorfas en este círculo;
el radical es elegido de manera que el término principal en el origen sea igual a
son entonces, holomorfas en este círculo;
el radical es elegido de manera que el término principal en el origen sea igual a ![]() . Decimos que estas funciones convergen uniformemente hacia una función holomorfa en
. Decimos que estas funciones convergen uniformemente hacia una función holomorfa en ![]() . Establezcamos, en efecto,
. Establezcamos, en efecto,
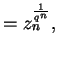 |
|||
![$\textstyle [R_{n+1}(z)]^{\frac{1}{q^{n+1}}}$](img373.png) |
de lo que se obtiene
![\begin{displaymath}
\frac{u_{n+1}}{u_n} = \left[\frac{1}{z_n}R^{\frac{1}{q}}(z_n)\right]^{\frac{1}{q^n}} = [H(z_n)]^{\frac{1}{q^n}}
\end{displaymath}](img375.png)
llamando a la función holomorfa ![]()
Por otra parte, evidentemente tenemos
![\begin{displaymath}
u_{n+1} = z\prod^{i=n}_{i=0}\frac{u_{i+1}}{u_i} = z\prod^{i=n}_{i=0}[H(z_i)]^{\frac{1}{q^i}}.
\end{displaymath}](img378.png)
Es suficiente entonces, probar la convergencia uniforme del producto infinito
cuyo término general es
![]() , es decir, de la serie cuyo término general es
, es decir, de la serie cuyo término general es
![]() ,
tomando la determinación del logaritmo la cual es nula en el origen. Como
,
tomando la determinación del logaritmo la cual es nula en el origen. Como ![]() tiende uniformemente a cero cuando
tiende uniformemente a cero cuando ![]() está en
está en ![]() y lo mismo sucede para
y lo mismo sucede para ![]() , tendremos, a partir de un cierto rango
, tendremos, a partir de un cierto rango ![]() ,
,
y
Debido a que
![]()
de lo anterior obtenemos
Luego entonces, la convergencia uniforme de la serie
 se demuestra inmediatamente, estando los
se demuestra inmediatamente, estando los
![]() limitados en su conjunto y decreciendo más rápido que los términos de una progresión geométrica convergente. Vemos finalmente que la serie de funciones
limitados en su conjunto y decreciendo más rápido que los términos de una progresión geométrica convergente. Vemos finalmente que la serie de funciones
![$[R_n(z)]^{\textstyle\frac{1}{q^n}}$](img390.png) converge hacia una función holomorfa
en
converge hacia una función holomorfa
en ![]() cuyo desarrollo en serie de Taylor alrededor del origen comienza por un término igual a
cuyo desarrollo en serie de Taylor alrededor del origen comienza por un término igual a ![]() . Si
. Si ![]() designa esta función límite,
tenemos2.1
designa esta función límite,
tenemos2.1
de donde
La existencia de esta función ![]() parece haber sido demostrada por
primera vez por M. Böttcher; dicha función desempeña un rol análogo a aquel de la función de Schröder2.2 para el caso de
parece haber sido demostrada por
primera vez por M. Böttcher; dicha función desempeña un rol análogo a aquel de la función de Schröder2.2 para el caso de ![]() . Si establecemos
. Si establecemos
![]() , obtenemos una representación conforme y biunívoca de un
círculo de centro O del plano
, obtenemos una representación conforme y biunívoca de un
círculo de centro O del plano ![]() sobre un dominio del plano de los
sobre un dominio del plano de los ![]() rodeando el origen y la substitución
rodeando el origen y la substitución ![]() es llevada nuevamente a la forma canónica:
es llevada nuevamente a la forma canónica: ![]() . Podemos llamar
puntos asociados a dos puntos que tienen igual el consecuente de rango
. Podemos llamar
puntos asociados a dos puntos que tienen igual el consecuente de rango ![]() ; en el plano de los
; en el plano de los ![]() , los asociados de un punto
, los asociados de un punto ![]() son los puntos
son los puntos
![]() que aunque damos a los enteros
que aunque damos a los enteros ![]() y
y ![]() todos los valores positivos, forman un conjunto denso sobre toda la circunferencia de
radio
todos los valores positivos, forman un conjunto denso sobre toda la circunferencia de
radio ![]() teniendo su centro en el origen. Si regresamos al plano de
la variable
teniendo su centro en el origen. Si regresamos al plano de
la variable ![]() vemos que, en un cierto dominio entorno al origen, los asociados de un punto son densos sobre una curva cerrada analítica
que pasa por este punto. Como dos puntos asociados son equivalentes respecto
al grupo
vemos que, en un cierto dominio entorno al origen, los asociados de un punto son densos sobre una curva cerrada analítica
que pasa por este punto. Como dos puntos asociados son equivalentes respecto
al grupo ![]() (
(![]() ) se sigue que este grupo no es estrictamente discontinuo
en un cierto dominio entorno del origen y, por consecuencia, también
en todos los dominios antecedentes, es decir en definitiva en todo dominio cerrado en el cual los
) se sigue que este grupo no es estrictamente discontinuo
en un cierto dominio entorno del origen y, por consecuencia, también
en todos los dominios antecedentes, es decir en definitiva en todo dominio cerrado en el cual los ![]() convergen uniformemente hacia un punto doble de multiplicador nulo. Existe entonces, desde este punto de vista, una diferencia esencial entre los puntos dobles de multiplicador nulo y los puntos dobles atractores de multiplicador no nulo.
convergen uniformemente hacia un punto doble de multiplicador nulo. Existe entonces, desde este punto de vista, una diferencia esencial entre los puntos dobles de multiplicador nulo y los puntos dobles atractores de multiplicador no nulo.
Daremos ahora algunas indicaciones sobre las curvas analíticas invariantes
pasando por un punto doble atractor. Si el multiplicador no es nulo, somos llevados a buscar las curvas analíticas invariantes mediante la substitución ![]() , y que pasan por el origen; si
, y que pasan por el origen; si ![]() es real, las rectas que pasan por el origen responden a la cuestión y son las únicas curvas regulares en el origen que gozan de esas propiedades. Les corresponde en el plano de la variable
es real, las rectas que pasan por el origen responden a la cuestión y son las únicas curvas regulares en el origen que gozan de esas propiedades. Les corresponde en el plano de la variable ![]() un haz de curvas analíticas pasando por el punto doble, regulares en ese punto e invariantes bajo la substitución
un haz de curvas analíticas pasando por el punto doble, regulares en ese punto e invariantes bajo la substitución ![]() . Si, por el contrario,
. Si, por el contrario, ![]() es imaginaria, no existe curva regular en el punto doble que responda a la cuestión, sino solamente curvas analíticas para las cuales este punto es un punto singular aislado, las más simples son aquellas que corresponden a las espirales logarítmicas del plano de la variable
es imaginaria, no existe curva regular en el punto doble que responda a la cuestión, sino solamente curvas analíticas para las cuales este punto es un punto singular aislado, las más simples son aquellas que corresponden a las espirales logarítmicas del plano de la variable ![]() representadas por la ecuación
representadas por la ecuación
![]() , donde
, donde ![]() designa una variable real en
designa una variable real en ![]() un punto fijo cualquiera, las curvas correspondientes del plano de las
un punto fijo cualquiera, las curvas correspondientes del plano de las ![]() son igualmente las espirales que tienen el punto doble por punto asintótico.
son igualmente las espirales que tienen el punto doble por punto asintótico.
En el caso ![]() , somos llevados al estudio de curvas invariantes mediante la substitución
, somos llevados al estudio de curvas invariantes mediante la substitución ![]() . Hay
. Hay ![]() curvas regulares en el origen, que responden a la cuestión; estas son las rectas de argumento
curvas regulares en el origen, que responden a la cuestión; estas son las rectas de argumento
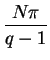 . Existen, además, espirales logarítmicas invariantes que tienen el origen por punto asintótico y cuya ecuación en coordenadas polares es
. Existen, además, espirales logarítmicas invariantes que tienen el origen por punto asintótico y cuya ecuación en coordenadas polares es
siendo ![]() una constante real arbitraria,
una constante real arbitraria, ![]() un entero al cual basta dar los valores
un entero al cual basta dar los valores
![]() . Regresando a la variable
. Regresando a la variable ![]() concluiremos con la existencia de
concluiremos con la existencia de ![]() curvas analíticas invariantes, regulares en el punto doble y cuyas tangentes en este punto forman un haz isogonal, estas son las únicas curvas invariantes que son regulares en el punto doble. Hay, además,
curvas analíticas invariantes, regulares en el punto doble y cuyas tangentes en este punto forman un haz isogonal, estas son las únicas curvas invariantes que son regulares en el punto doble. Hay, además, ![]() haces de curvas. Existen, además,
haces de curvas. Existen, además, ![]() haces de curvas espirales invariantes que tienen el punto doble por punto asintótico y cuyas ecuaciones se escriben simplemente con ayuda del módulo y del argumento de la función
haces de curvas espirales invariantes que tienen el punto doble por punto asintótico y cuyas ecuaciones se escriben simplemente con ayuda del módulo y del argumento de la función ![]() .
.
Consideremos ahora un ciclo de puntos
![]() de multiplicador más pequeño, en módulo, que la unidad; sean
de multiplicador más pequeño, en módulo, que la unidad; sean ![]() un pequeño dominio circular de centro
un pequeño dominio circular de centro ![]() ;
;
![]() los dominios consecuentes que encierran respectivamente los puntos
los dominios consecuentes que encierran respectivamente los puntos
![]() . Si el diámetro de
. Si el diámetro de ![]() es suficientemente pequeño, los dominios
es suficientemente pequeño, los dominios
![]() son encajados unos en otros; lo mismo sucede para
son encajados unos en otros; lo mismo sucede para
![]() y en general de
y en general de
![]() . Además, el diámetro de
. Además, el diámetro de ![]() tiende a cero con
tiende a cero con
![]() , de suerte que
, de suerte que ![]() siendo interior a uno de los dominios
siendo interior a uno de los dominios
![]() ,
, ![]() converge periódicamente y de manera uniforme hacia el sistema de las
converge periódicamente y de manera uniforme hacia el sistema de las ![]() constantes (
constantes (
![]() ). Si el multiplicador no es nulo, demostramos que existe un sistema de
). Si el multiplicador no es nulo, demostramos que existe un sistema de ![]() funciones holomorfas respectivamente en los dominios
funciones holomorfas respectivamente en los dominios
![]() y de derivadas no nulas en estos puntos que satisfacen las ecuaciones funcionales
y de derivadas no nulas en estos puntos que satisfacen las ecuaciones funcionales
de donde
Todo lo anterior supone a ![]() definida y uniforme en todo el plano, por ejemplo racional. Este resultado se deduce fácilmente de la ecuación de Schröder en el caso de un punto doble, señalando que los puntos
definida y uniforme en todo el plano, por ejemplo racional. Este resultado se deduce fácilmente de la ecuación de Schröder en el caso de un punto doble, señalando que los puntos
![]() son puntos dobles de la substitución
son puntos dobles de la substitución
![]() .
.
Ahora vamos a estudiar la iteración de una substitución uniforme en la vecindad de un punto doble de multiplicador igual, en módulo, a la unidad, comenzando por el caso más simple, aquel de ![]() . Este estudio ha sido realizado por M. Leau en su Tesis; vamos a retomar su análisis bajo una forma diferente y completar, sobre muchos puntos, los resultados obtenidos por este eminente geómetra.
. Este estudio ha sido realizado por M. Leau en su Tesis; vamos a retomar su análisis bajo una forma diferente y completar, sobre muchos puntos, los resultados obtenidos por este eminente geómetra.
Sea ![]() un punto doble en la vecindad del cual tenemos
un punto doble en la vecindad del cual tenemos
Primero nos situaremos en el caso donde ![]() no es nulo (con esta condición demostramos muy fácilmente el caracter de invariancia) y para mayor comodidad asumiremos que
no es nulo (con esta condición demostramos muy fácilmente el caracter de invariancia) y para mayor comodidad asumiremos que ![]() está confinada al infinito por una transformación homográfica previa.
Tendremos entonces
está confinada al infinito por una transformación homográfica previa.
Tendremos entonces
Siempre podemos orientar los ejes de manera que ![]() sea real y positiva. Finalmente existe interés en estudiar el caso un poco más general donde la substitución es de la forma
sea real y positiva. Finalmente existe interés en estudiar el caso un poco más general donde la substitución es de la forma
siendo ![]() una función que puede tener un punto crítico en el infinito, pero tal que
una función que puede tener un punto crítico en el infinito, pero tal que
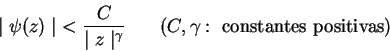
Además el infinito, para esta función, es un punto singular aislado. Sea ![]() el radio de un círculo
el radio de un círculo ![]() de centro
de centro ![]() tal que
tal que ![]() sea holomorfo y uniforme en el dominio
sea holomorfo y uniforme en el dominio ![]() exterior a dicho círculo donde hemos trazado un corte del punto
exterior a dicho círculo donde hemos trazado un corte del punto ![]() al infinito negativo siguiendo el eje real. Sea
al infinito negativo siguiendo el eje real. Sea ![]() un punto de este dominio y busquemos en que condición los consecuentes sucesivos de
un punto de este dominio y busquemos en que condición los consecuentes sucesivos de ![]() , estarán aún contenidos en el mencionado dominio. Llamemos
, estarán aún contenidos en el mencionado dominio. Llamemos ![]() al módulo máximo de
al módulo máximo de ![]() en este dominio; si
en este dominio; si ![]() es suficientemente grande, tendremos
es suficientemente grande, tendremos ![]() , que es lo que supondremos. El punto
, que es lo que supondremos. El punto ![]() está en el interior de un círculo de centro
está en el interior de un círculo de centro ![]() y de radio
y de radio ![]() 2.3;
2.3; ![]() es exterior a este círculo. Si este círculo es interior al dominio
es exterior a este círculo. Si este círculo es interior al dominio ![]() , el punto
, el punto ![]() se encontrará en el interior de un segundo círculo teniendo por centro
se encontrará en el interior de un segundo círculo teniendo por centro ![]() y por radio
y por radio ![]() ; en general, el punto
; en general, el punto ![]() será interior al círculo de centro
será interior al círculo de centro ![]() y radio
y radio ![]() , siempre que todos los círculos precedentes sean interiores a
, siempre que todos los círculos precedentes sean interiores a ![]() . Todos estos círculos están comprendidos en el ángulo de dos semirectas resultantes del punto
. Todos estos círculos están comprendidos en el ángulo de dos semirectas resultantes del punto ![]() y haciendo con
y haciendo con ![]() un ángulo agudo
un ángulo agudo ![]() cuyo seno es igual a
cuyo seno es igual a ![]() (figura I).
(figura I).
Para que la condición buscada esté completa, basta que este ángulo no tenga ningún punto en común con ![]() . Los puntos
. Los puntos ![]() para los cuales así es, son interiores al dominio
para los cuales así es, son interiores al dominio ![]() definido como sigue: tracemos las dos tangentes al círculo
definido como sigue: tracemos las dos tangentes al círculo ![]() que hacen con
que hacen con ![]() ángulos iguales a
ángulos iguales a ![]() y que se cortan sobre la parte positiva de
y que se cortan sobre la parte positiva de ![]() ; sean
; sean ![]() ,
, ![]() las partes de estas tangentes comprendidas entre los puntos de contacto y el infinito hacia las
las partes de estas tangentes comprendidas entre los puntos de contacto y el infinito hacia las ![]() negativas; el dominio
negativas; el dominio ![]() está limitado por
está limitado por ![]() ,
, ![]() , el arco
, el arco ![]() y se extiende al infinito hacia las
y se extiende al infinito hacia las ![]() positivas (figura I). Enseguida podemos hacer crecer el radio de círculo
positivas (figura I). Enseguida podemos hacer crecer el radio de círculo ![]() desde su valor inicial
desde su valor inicial ![]() hasta el infinito; tendremos, en virtud de las hipótesis hechas sobre
hasta el infinito; tendremos, en virtud de las hipótesis hechas sobre ![]() :
:

para todos los valores de ![]() de radio comprendido en el intervalo
de radio comprendido en el intervalo ![]() . Como podemos reemplazar el máximo
. Como podemos reemplazar el máximo ![]() de
de
![]() por un número más grande, podemos definir constantemente la inclinación
por un número más grande, podemos definir constantemente la inclinación ![]() de la recta
de la recta ![]() por la fórmula
por la fórmula

Esta recta, que tiene por ecuación
![]() incluye un arco de curva parabólica cuyo radio de curvatura
no cambia de signo, pues tiene por expresión
incluye un arco de curva parabólica cuyo radio de curvatura
no cambia de signo, pues tiene por expresión ![]()
![]() o, en virtud de la relación entre
o, en virtud de la relación entre ![]() y
y ![]() ,
,
![\begin{displaymath}
\gamma\rho \left[ 1 + (\gamma + 1)\frac{\cos^2\omega}{\sin^2\omega}\right],
\end{displaymath}](img463.png)
cantidad esencialmente positiva. La curva es entonces convexa. De lo cual podemos deducir que el dominio total, suma de los dominios análogos a ![]() , cuando hacemos variar
, cuando hacemos variar ![]() , está limitado por los dos arcos parabólicos
, está limitado por los dos arcos parabólicos ![]() ,
, ![]() extendiendose al infinito por la izquierda, los dos segmentos de recta
extendiendose al infinito por la izquierda, los dos segmentos de recta ![]() ,
, ![]() y el arco del círculo
y el arco del círculo ![]() (figura II).
(figura II).
Sea ![]() el dominio así limitado y extendiendose hacia la derecha. Vamos a mostrar que los consecuentes de un punto de
el dominio así limitado y extendiendose hacia la derecha. Vamos a mostrar que los consecuentes de un punto de ![]() tienden hacia infinito, siendo la convergencia uniforme en todo dominio cerrado
tienden hacia infinito, siendo la convergencia uniforme en todo dominio cerrado ![]() interior a
interior a ![]() y limitado hacia las
y limitado hacia las ![]() negativas. El dominio
negativas. El dominio ![]() , según la manera en que ha sido obtenido, contiene los consecuentes de todos sus puntos, igual que los dominios
, según la manera en que ha sido obtenido, contiene los consecuentes de todos sus puntos, igual que los dominios ![]() ; además, todo dominio tal que
; además, todo dominio tal que ![]() forma parte de un dominio
forma parte de un dominio ![]() ; finalmente, en todo el dominio
; finalmente, en todo el dominio ![]() , los módulos de las cantidades
, los módulos de las cantidades
![]() permanecen inferiores a un número fijo
permanecen inferiores a un número fijo ![]() inferior a
inferior a ![]() . Hechas estas observaciones, la proposición anunciada es inmediata. Tenemos en efecto,
. Hechas estas observaciones, la proposición anunciada es inmediata. Tenemos en efecto,
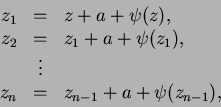
de donde
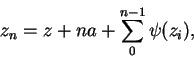
y, tomando las partes reales de los dos miembros,
![\begin{displaymath}
x_n = x + na \sum_0^{n-1}\Re[\psi(z_i)] \hspace{0.3in} (z_n = x_n + iy_n).
\end{displaymath}](img472.png)
Como la parte real de ![]() queda comprendida entre
queda comprendida entre ![]() y
y ![]() y además por otra parte, en
y además por otra parte, en ![]() tenemos
tenemos ![]() , con
, con ![]() finita y positiva, obtenemos de la igualdad precedente
finita y positiva, obtenemos de la igualdad precedente
y esta última expresión es infinita positiva al mismo tiempo que ![]() , ya que
, ya que ![]() . Entonces
. Entonces ![]() y
y ![]() tienden uniformemente hacia infinito cuando
tienden uniformemente hacia infinito cuando ![]() está en
está en ![]() . Podemos señalar que tendremos, a partir de un cierto rango,
. Podemos señalar que tendremos, a partir de un cierto rango,
![]() , si
, si
![]() ; podemos también escribir
; podemos también escribir
![]()
![]()
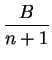 para todos los valores de
para todos los valores de ![]() , siendo
, siendo ![]() una constante. Es entonces fácil obtener el valor asintótico de
una constante. Es entonces fácil obtener el valor asintótico de ![]() , pues según la igualdad
, pues según la igualdad
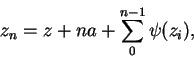
tendremos
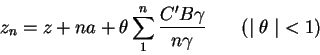
ó
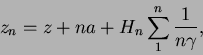
siendo ![]() una cantidad uniformemente acotada. De lo que resulta, suponiendo
una cantidad uniformemente acotada. De lo que resulta, suponiendo
![]() ,
,
siendo ![]() uniformemente acotada. Si el dominio
uniformemente acotada. Si el dominio ![]() es acotado, también podemos escribir
es acotado, también podemos escribir
siendo siempre ![]() uniformemente acotado;
uniformemente acotado; ![]() tiene entonces por valor asintótico
tiene entonces por valor asintótico ![]() y el argumento de
y el argumento de ![]() tiende uniformemente hacia cero. Para
tiende uniformemente hacia cero. Para ![]() las dos últimas fórmulas permanecen exactas si reemplazamos
las dos últimas fórmulas permanecen exactas si reemplazamos ![]() por
por ![]() (logaritmo neperiano de
(logaritmo neperiano de ![]() ).
).
Es importante precisar más, la expresión asintótica obtenida en la hipótesis de ![]() . De una manera más precisa, supondremos
. De una manera más precisa, supondremos

Establezcamos
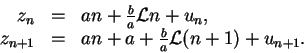
Reemplazando ![]() y
y ![]() por expresiones en la ecuación
por expresiones en la ecuación
obtenemos
En el segundo miembro, el primer término es el término general de una serie numérica absolutamente convergente; tenemos, en efecto,
El segundo término es el de una serie uniformememte convergente en el dominio acotado ![]() , ya que puede ser escrito
, ya que puede ser escrito
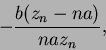
y por tanto
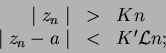
con ![]() y
y ![]() independientes de
independientes de ![]() y de
y de ![]() ; este término es entonces comparable a
; este término es entonces comparable a
![]() , término general de una serie convergente.
, término general de una serie convergente.
La misma observación para el tercer término, ya que tenemos
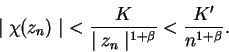
Como tenemos
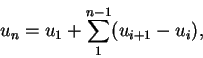
![]() tiene un límite para
tiene un límite para ![]() infinito que es la suma de una serie uniformemente convergente de funciones holomorfas en
infinito que es la suma de una serie uniformemente convergente de funciones holomorfas en ![]() el cual es entonces él mismo una función en
el cual es entonces él mismo una función en ![]() . Si
. Si ![]() designa esta función, holomorfa en todo punto interior a
designa esta función, holomorfa en todo punto interior a ![]() , podemos escribir
, podemos escribir
Cambiemos ![]() por
por ![]() y
y ![]() por
por ![]() , en esta desigualdad, con lo que tenemos
, en esta desigualdad, con lo que tenemos
Cercenando miembro a miembro y pasando al límite, obtenemos la ecuación funcional
que es la ecuación de Abel.
Así la ecuación de Abel, relativa a la substitución ![]() , es satisfecha por una función
, es satisfecha por una función ![]() holomorfa en
holomorfa en ![]() , para la cual el punto en el infinito es además un punto singular transcendente.
, para la cual el punto en el infinito es además un punto singular transcendente.
Señalemos de inmediato que si ![]() tiene simplemente como singularidad un polo en el punto al infinito, podremos elegir el círculo
tiene simplemente como singularidad un polo en el punto al infinito, podremos elegir el círculo ![]() suficientemente grande para que el exterior de este círculo
suficientemente grande para que el exterior de este círculo ![]() no tome más que una sola vez cada valor; lo mismo sucederá en el dominio
no tome más que una sola vez cada valor; lo mismo sucederá en el dominio ![]() para las funciones iteradas, y por consecuencia también para las funciones
para las funciones iteradas, y por consecuencia también para las funciones
siendo ![]() el límite uniformemente alcanzado de estas últimas funciones, también no tomará más que una vez cada valor en
el límite uniformemente alcanzado de estas últimas funciones, también no tomará más que una vez cada valor en ![]() 2.4. Vamos a estudiar los valores asintóticos de esta función cuando
2.4. Vamos a estudiar los valores asintóticos de esta función cuando ![]() tiende al infinito permaneciendo en un dominio
tiende al infinito permaneciendo en un dominio ![]() acotado hacia las
acotado hacia las ![]() negativas, por ejemplo en el dominio definido por
negativas, por ejemplo en el dominio definido por
![]() . Tendremos en estas condiciones
. Tendremos en estas condiciones
con
![]() designando un (término) infinitamente grande que es a lo más del orden de
designando un (término) infinitamente grande que es a lo más del orden de
![]() . Para el denominador, señalemos que tenemos por definición
. Para el denominador, señalemos que tenemos por definición
![\begin{displaymath}
F(z) = \lim_{n=\infty}\left[ z_n - \frac{b}{a}{\cal L}n - na \right].
\end{displaymath}](img521.png)
Enseguida tenemos
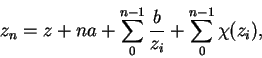
de donde
![\begin{displaymath}
F(z) - z = \lim_{n=\infty}\left[ \sum_0^{n-1}\frac{b}{z_i} - \frac{b}{a}{\cal L}n + \sum_0^{n-1}\chi(z_i) \right].
\end{displaymath}](img523.png)
La serie ![]() converge uniformemente en el dominio no acotado
converge uniformemente en el dominio no acotado ![]() y representa una función acotada en ese dominio; podemos entonces ignorarla. Podemos por otra parte reemplazar
y representa una función acotada en ese dominio; podemos entonces ignorarla. Podemos por otra parte reemplazar
![]()
![]() por
por
![]()
![]() , puesto que la diferencia de estas dos cantidades tiende a una constante finita. Podemos por último ignorar el factor
, puesto que la diferencia de estas dos cantidades tiende a una constante finita. Podemos por último ignorar el factor ![]() y somos llevados a estudiar la función representada por la serie
y somos llevados a estudiar la función representada por la serie
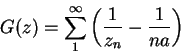
(suprimiendo el primer término en ![]() ).
).
Podemos admitir que los ![]() van creciendo con
van creciendo con ![]() 2.5, es decir (dado que el dominio
2.5, es decir (dado que el dominio ![]() contiene sus consecuentes) siempre tenemos
contiene sus consecuentes) siempre tenemos
![]() . Vemos fácilmente, por una representación geométrica, que esta condición será cumplida si
. Vemos fácilmente, por una representación geométrica, que esta condición será cumplida si
ó
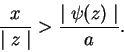
Como tenemos
![]()
![]() , basta que tengamos
, basta que tengamos ![]()
![]() . Supondremos entonces, para simplificar el análisis siguiente, que tomamos
. Supondremos entonces, para simplificar el análisis siguiente, que tomamos ![]()
![]() . Así que
. Así que ![]() van creciendo con
van creciendo con ![]() .
Sentado lo anterior, podemos escribir
.
Sentado lo anterior, podemos escribir
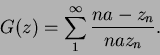
Pero, en virtud del parágrafo precedente, tenemos
los ![]() siendo uniformemente acotados cuando
siendo uniformemente acotados cuando ![]() está en
está en ![]() . La serie que define
. La serie que define ![]() se descompone en dos
se descompone en dos
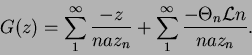
Como tenemos
![]() y
y
![]() , la segunda serie representa una función de
, la segunda serie representa una función de ![]() acotada (inferior a
acotada (inferior a
 , cantidad finita). Basta entonces considerar la primera.
, cantidad finita). Basta entonces considerar la primera.
Establezcamos
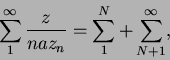
siendo el entero ![]() la parte entera de
la parte entera de ![]() . La primera suma parcial es inferior en módulo a
. La primera suma parcial es inferior en módulo a
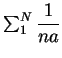 , puesto que
, puesto que
![]() ; luego entonces
; luego entonces
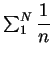 es igual, ignorando las cantidades acotadas, a
es igual, ignorando las cantidades acotadas, a ![]() ó a
ó a
![]() . La segunda suma parcial es inferior en módulo a
. La segunda suma parcial es inferior en módulo a
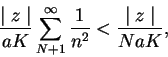
cantidad acotada ya que
![]() tiende a
tiende a ![]() .
.
Obtenemos entonces finalmente
con ![]() constante finita positiva y, lo que viene a ser lo mismo que,
constante finita positiva y, lo que viene a ser lo mismo que,
En el caso particular donde ![]() , igual obtenemos
, igual obtenemos
Vamos a demostrar ahora que, aunque ![]() tiende hacia el infinito permaneciendo siempre en el mismo dominio
tiende hacia el infinito permaneciendo siempre en el mismo dominio ![]()
![]() considerado anteriormente, la derivada
considerado anteriormente, la derivada ![]() tiende hacia la unidad. Admitiremos que
tiende hacia la unidad. Admitiremos que ![]() es desarrollable en serie ordenada según las potencias decrecientes de
es desarrollable en serie ordenada según las potencias decrecientes de ![]() :
:
ciertos exponentes ![]() pudiendo además no ser enteros, aunque siendo el segundo miembro derivable término a término,
pudiendo además no ser enteros, aunque siendo el segundo miembro derivable término a término,
Para no descartar el caso de ![]() , llamemos
, llamemos ![]() la primera potencia de
la primera potencia de ![]() cuyo coeficiente no sea nulo en ese desarrollo. Para valores grandes de
cuyo coeficiente no sea nulo en ese desarrollo. Para valores grandes de ![]() ,
, ![]() estará comprendido entre
estará comprendido entre
![]() y
y
![]() siendo
siendo ![]() y
y ![]() constantes finitas positivas2.6 con
constantes finitas positivas2.6 con ![]() al menos igual a
al menos igual a ![]() . Tendremos entonces
. Tendremos entonces
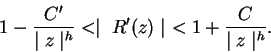
Luego entonces ![]() es el límite de
es el límite de ![]() para
para ![]() infinito y tenemos
infinito y tenemos
![]() y por consecuencia todos los
y por consecuencia todos los ![]() siendo asumidos suficientemente grandes para que las desigualdades precedentes sean aplicables, tendremos
siendo asumidos suficientemente grandes para que las desigualdades precedentes sean aplicables, tendremos

![]() tiene entonces un valor comprendido entre aquellos dos productos infinitos
tiene entonces un valor comprendido entre aquellos dos productos infinitos
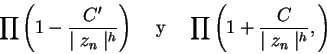
y, para probar que ![]() tiende a
tiende a ![]() para
para ![]() infinito, basta probar que la suma de la serie
infinito, basta probar que la suma de la serie
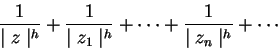
tiende a cero con
![]() . De lo anterior resultan desigualdades bien conocidas
. De lo anterior resultan desigualdades bien conocidas
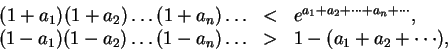
donde las ![]() están comprendidas entre
están comprendidas entre ![]() y
y ![]() . Luego entonces este último punto es muy fácil de establecer, pues si dividimos esta serie en dos partes como anteriormente
. Luego entonces este último punto es muy fácil de establecer, pues si dividimos esta serie en dos partes como anteriormente
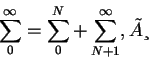
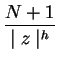 (puesto que
(puesto que
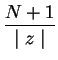 que tiende hacia
que tiende hacia  , que tiende a cero. En cuanto a la segunda, en virtud de
, que tiende a cero. En cuanto a la segunda, en virtud de
Relativamente a esta demostración y a aquella que precede, señalemos que el resultado subsiste si ![]() tiende hacia el infinito pemaneciendo en un dominio
tiende hacia el infinito pemaneciendo en un dominio ![]() interior a
interior a ![]() y acotado hacia los
y acotado hacia los ![]() negativos, sin que sea necesaria la condición suplementaria
negativos, sin que sea necesaria la condición suplementaria
![]() impuesta a la frontera inferior de las
impuesta a la frontera inferior de las ![]() de los puntos de
de los puntos de ![]() . Pues el
. Pues el ![]() -ésimo consecuente de algún dominio de
-ésimo consecuente de algún dominio de ![]() será siempre interior a un dominio
será siempre interior a un dominio ![]() que satisface esta condición suplementaria siempre que
que satisface esta condición suplementaria siempre que ![]() sea suficientemente grande, y las ecuaciones funcionales
sea suficientemente grande, y las ecuaciones funcionales
![\begin{displaymath}
\begin{array}{rcl}
F[R(z)] & = & F(z) + a, \\
F'[R(z)] & = & \frac{1}{R'(z)} F'(z)
\end{array}\end{displaymath}](img589.png)
muestran que las funciones ![]() y
y ![]() satisfacen las proposiciones límite que acabamos de examinar, la longitud de un camino
satisfacen las proposiciones límite que acabamos de examinar, la longitud de un camino ![]() , si satisfacen las proposiciones límites la longitud del camino consecuente
, si satisfacen las proposiciones límites la longitud del camino consecuente ![]() . Por ejemplo, si
. Por ejemplo, si
tenemos
que puede ser escrito
![]() , puesto que
, puesto que ![]() y
y ![]() no difieren más que por una cantidad acotada.
no difieren más que por una cantidad acotada.
Ahora vamos a estudiar, en un dominio ![]() , las curvas invariantes para la substitución dada. Supongamos
, las curvas invariantes para la substitución dada. Supongamos ![]() regular en el infinito. En estas condiciones podemos tomar a
regular en el infinito. En estas condiciones podemos tomar a ![]() suficientemente grande para que, en el dominio cerrado
suficientemente grande para que, en el dominio cerrado
![]() tienda uniformemente hacia el infinito;
tienda uniformemente hacia el infinito; ![]() la función
la función ![]() de Abel no tome más que una sola vez cada valor;
de Abel no tome más que una sola vez cada valor; ![]() la parte real de
la parte real de ![]() sea positiva (puesto que tiende hacia
sea positiva (puesto que tiende hacia ![]() cuando la parte real de
cuando la parte real de ![]() tiende hacia
tiende hacia ![]() ). Si establecemos entonces
). Si establecemos entonces ![]() , obtenemos una representación conforme y biunívoca del dominio
, obtenemos una representación conforme y biunívoca del dominio ![]() sobre una región simplemente conexa y no acotada del plano de las
sobre una región simplemente conexa y no acotada del plano de las ![]() , teniendo por frontera la curva
, teniendo por frontera la curva ![]() que corresponde a la recta
que corresponde a la recta ![]() . Esta curva
. Esta curva ![]() es cortada en un punto y en uno solo por toda paralela al eje de las
es cortada en un punto y en uno solo por toda paralela al eje de las ![]() ; en efecto, sea
; en efecto, sea
La curva ![]() es representada por
es representada por
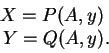
En razón de la expresión asintótica
![]() ,
, ![]() toma valores infinitamente grandes al mismo tiempo que
toma valores infinitamente grandes al mismo tiempo que ![]() es del mismo signo;
es del mismo signo; ![]() toma entonces todos los valores reales cuando
toma entonces todos los valores reales cuando ![]() crece de
crece de ![]() a
a ![]() . Si
. Si ![]() estuviera cortada en dos puntos por una paralela al eje de las
estuviera cortada en dos puntos por una paralela al eje de las ![]() , tendríamos en estos dos puntos
, tendríamos en estos dos puntos
Tendríamos entonces, para un valor ![]() comprendido entre
comprendido entre ![]() y
y ![]() ,
,
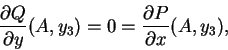
lo que es imposible, ya que
![]() permanece positiva sobre la recta
permanece positiva sobre la recta ![]() . Vemos también que la dirección límite de la tangente a
. Vemos también que la dirección límite de la tangente a ![]() , cuando se aleja al infinito, es paralela al eje de las
, cuando se aleja al infinito, es paralela al eje de las ![]() , puesto que tenemos sobre esta curva
, puesto que tenemos sobre esta curva
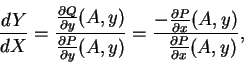
y esta relación tiende al infinito con ![]() puesto que el numerador tiende a
puesto que el numerador tiende a ![]() y el denominador hacia cero. Esta curva
y el denominador hacia cero. Esta curva ![]() particiona entonces el plano de las
particiona entonces el plano de las ![]() en dos regiones, una de las cuales es
en dos regiones, una de las cuales es ![]() , aquella se extiende al infinito hacia las
, aquella se extiende al infinito hacia las ![]() positivas, corresponde al dominio
positivas, corresponde al dominio ![]() . En el haz de las rectas paralelas al eje de las
. En el haz de las rectas paralelas al eje de las ![]() en
en ![]() corresponde en
corresponde en ![]() un haz de curvas invariantes para la substitución
un haz de curvas invariantes para la substitución
![]() . Estas curvas tienen por ecuación
. Estas curvas tienen por ecuación ![]() const. Pasa una y sólo una curva por cada punto de
const. Pasa una y sólo una curva por cada punto de ![]() y se extienden desde la recta
y se extienden desde la recta ![]() hasta el infinito. Tenemos sobre esas curvas
hasta el infinito. Tenemos sobre esas curvas
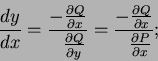
![]() no es entonces jamás infinita y tiende a cero cuando nos alejamos al infinito sobre la curva; la dirección límite de la tangente es entonces paralela a
no es entonces jamás infinita y tiende a cero cuando nos alejamos al infinito sobre la curva; la dirección límite de la tangente es entonces paralela a ![]() . Dicha tangente contiene naturalmente los consecuentes de todos los puntos y también los antecedentes hasta un cierto rango; estos puntos corresponden a los puntos
. Dicha tangente contiene naturalmente los consecuentes de todos los puntos y también los antecedentes hasta un cierto rango; estos puntos corresponden a los puntos ![]() del plano de las
del plano de las ![]() , tomando
, tomando ![]() todos los valores enteros positivos (lo que da los puntos homólogos de los consecuentes de
todos los valores enteros positivos (lo que da los puntos homólogos de los consecuentes de ![]() ) y ciertos valores negativos para los cuales
) y ciertos valores negativos para los cuales ![]() permanece interior a
permanece interior a ![]() (lo que da los homólogos de los antecedentes de
(lo que da los homólogos de los antecedentes de ![]() interiores a
interiores a ![]() ). Esta representación da inmediatamente el medio para definir
). Esta representación da inmediatamente el medio para definir ![]() para los valores no enteros de
para los valores no enteros de ![]() . Basta substituir en el grupo discontinuo de translaciones
. Basta substituir en el grupo discontinuo de translaciones
![]() , el grupo continuo de las translaciones representadas por la misma fórmula, siendo
, el grupo continuo de las translaciones representadas por la misma fórmula, siendo ![]() un parámetro continuo. Resolvemos así el problema de la iteración analítica. En efecto, sea
un parámetro continuo. Resolvemos así el problema de la iteración analítica. En efecto, sea ![]() la función inversa de
la función inversa de ![]() que da la representación conforme de
que da la representación conforme de ![]() sobre
sobre ![]() . De la ecuación de Abel
. De la ecuación de Abel
deducimos
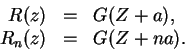
Esta última igualdad permite definir ![]() para un
para un ![]() cualquiera a través de una función analítica de
cualquiera a través de una función analítica de ![]() y de
y de ![]() . Tendremos siempre
. Tendremos siempre
puesto que los dos miembros de esta igualdad designan dos puntos que tienen por homólogos, en el plano de las ![]() ,
,
es decir el mismo punto.
Ahora examinemos como se desarrollan las cosas cuando el punto doble ![]() de multiplicador
de multiplicador ![]() [con
[con
![]() ] está a una distancia finita. Podemos suponer
] está a una distancia finita. Podemos suponer ![]() y
y
estando orientados los ejes de manera que ![]() sea real y positiva. El cambio de variables
sea real y positiva. El cambio de variables
![]() nos lleva a la forma
nos lleva a la forma
Basta entonces aplicar los resultados del parágrafo precedente para poder enunciar lo siguiente: Existe un dominio ![]() limitado por un contorno simple, formado por ejemplo de arcos analíticos, y presentando en
limitado por un contorno simple, formado por ejemplo de arcos analíticos, y presentando en ![]() un punto reentrante2.8 con una tangente dirigida siguiendo la parte negativa del eje real que goza de la propiedad de que los consecuentes de un punto de
un punto reentrante2.8 con una tangente dirigida siguiendo la parte negativa del eje real que goza de la propiedad de que los consecuentes de un punto de ![]() (incluidos los puntos frontera junto con el origen) son interiores a
(incluidos los puntos frontera junto con el origen) son interiores a ![]() y tienden hacia el origen cuando el índice de iteración crece indefinidamente; la convergencia es uniforme en todo dominio cerrado interior a
y tienden hacia el origen cuando el índice de iteración crece indefinidamente; la convergencia es uniforme en todo dominio cerrado interior a ![]() cuya frontera no contiene el origen. Existen además otros dominios
cuya frontera no contiene el origen. Existen además otros dominios ![]() formados, por ejemplo, por el interior de un círculo tangente en
formados, por ejemplo, por el interior de un círculo tangente en ![]() al eje imaginario del lado de las
al eje imaginario del lado de las ![]() positivas, y gozando de las mismas propiedades que
positivas, y gozando de las mismas propiedades que ![]() , la convergencia uniforme de los consecuentes de un punto que tiene lugar además para todo el dominio cerrado
, la convergencia uniforme de los consecuentes de un punto que tiene lugar además para todo el dominio cerrado ![]() (incluido el origen).
(incluido el origen).
Si aplicamos estos resultados a la función inversa de ![]() , o más exactamente a la rama de la función inversa nula en el origen y representada por la serie
, o más exactamente a la rama de la función inversa nula en el origen y representada por la serie
obtenemos un resultado análogo, a aquel excepto que los dominios ![]() y
y ![]() que reemplazan a
que reemplazan a ![]() y
y ![]() tienen una disposición simétrica de estos últimos con relación al origen; estos son dominios de convergencia simple o uniforme para los antecedentes de un punto obtenidos a través de la rama de la función
tienen una disposición simétrica de estos últimos con relación al origen; estos son dominios de convergencia simple o uniforme para los antecedentes de un punto obtenidos a través de la rama de la función ![]() que acabamos de definir (figura III).
que acabamos de definir (figura III).
Los dominios ![]() y
y ![]() tienen en común dos sectores de ángulo en
el vértice
tienen en común dos sectores de ángulo en
el vértice
![]() en los cuales los
en los cuales los ![]() convergen hacia cero (uniformemente o no), mientras que los
convergen hacia cero (uniformemente o no), mientras que los ![]() convergen uniformemente hacia cero. De igual manera
convergen uniformemente hacia cero. De igual manera ![]() y
y ![]() tienen en común dos sectores de ángulo en el vértice
tienen en común dos sectores de ángulo en el vértice
![]() en los cuales los
en los cuales los ![]() convergen uniformemente hacia cero, mientras que los
convergen uniformemente hacia cero, mientras que los ![]() convergen hacia cero (uniformemente o no).
convergen hacia cero (uniformemente o no).
Los consecuentes de un punto de ![]() están distribuidos sobre las curvas invariantes tangentes en
están distribuidos sobre las curvas invariantes tangentes en ![]() en el eje real del lado de las
en el eje real del lado de las ![]() positivas; observación análoga para los antecedentes.
positivas; observación análoga para los antecedentes.
Los ![]() tienen por expresión asintótica
tienen por expresión asintótica
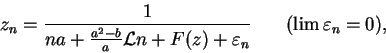
siendo ![]() una función holomorfa en el interior de
una función holomorfa en el interior de ![]() , que satisface la ecuación de Abel
, que satisface la ecuación de Abel
Si ![]() tiende hacia el origen permaneciendo en el interior del círculo
tiende hacia el origen permaneciendo en el interior del círculo ![]() , tenemos
, tenemos
Ahora vamos a estudiar el caso de un punto doble para el cual tenemos
Llevando este punto al origen, tenemos
Se asume que los ejes están orientados de manera que ![]() sea real y positiva. Cambiando
sea real y positiva. Cambiando ![]() y
y ![]() por
por
![]() y
y
![]() de manera que confinemos al punto doble al infinito, tenemos
de manera que confinemos al punto doble al infinito, tenemos


de lo que se obtiene
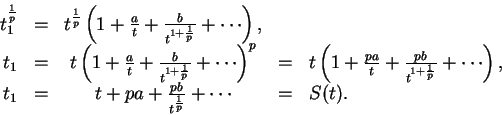
Con ![]() ordenada, a partir del tercer término según las potencias negativas descendentes de
ordenada, a partir del tercer término según las potencias negativas descendentes de
![]() cae nuevamente en la categoría de las funciones estudiadas en el parágrafo 8 que dan lugar a un algoritmo convergente en un dominio
cae nuevamente en la categoría de las funciones estudiadas en el parágrafo 8 que dan lugar a un algoritmo convergente en un dominio ![]() que hemos descrito y que deja en su exterior la parte negativa del eje real. Si
que hemos descrito y que deja en su exterior la parte negativa del eje real. Si ![]() varía en este dominio, su argumento varía entre
varía en este dominio, su argumento varía entre ![]() y
y ![]() límites excluidos, y las
límites excluidos, y las ![]() determinaciones de
determinaciones de
![]() quedan respectivamente en el interior de
quedan respectivamente en el interior de ![]() sectores de vértice
sectores de vértice ![]() de ángulo
de ángulo
![]() . Elijamos una de estas determinaciones, por ejemplo aquella cuyo argumento está comprendido entre
. Elijamos una de estas determinaciones, por ejemplo aquella cuyo argumento está comprendido entre
![]() y
y
![]() , y llevemos este valor de
, y llevemos este valor de ![]() a la fórmula
a la fórmula
que equivale a
![]() , llamando
, llamando ![]() a la determinación que acabamos de elegir
a la determinación que acabamos de elegir
![]() . Con
. Con ![]() interior a
interior a ![]()
![]() admite una determinación cuyo argumento está comprendido (límites excluidos) entre
admite una determinación cuyo argumento está comprendido (límites excluidos) entre
![]() y
y
![]() como aquel de
como aquel de ![]() . Tenemos entonces para esta elección del radical
. Tenemos entonces para esta elección del radical
siendo ![]() una raíz
una raíz ![]() -ésima de la unidad. Decimos que
-ésima de la unidad. Decimos que ![]() . En efecto, si
. En efecto, si ![]() , permanece interior a
, permanece interior a ![]() , se aleja hacia el infinito, por ejemplo siguiendo la parte positiva del eje real; de la forma
, se aleja hacia el infinito, por ejemplo siguiendo la parte positiva del eje real; de la forma ![]() se obtiene que
se obtiene que ![]() llega a ser infinito con el mismo argumento límite que
llega a ser infinito con el mismo argumento límite que ![]() . Es decir cero. Por otra parte,
. Es decir cero. Por otra parte,
![]() y
y
![]() tendrán argumentos límites iguales a
tendrán argumentos límites iguales a
![]() según la elección. Por último según la forma de
según la elección. Por último según la forma de ![]() ,
, ![]() tendrá el mismo argumento límite que
tendrá el mismo argumento límite que ![]() . Entonces finalmente con
. Entonces finalmente con
![]() y
y ![]() teniendo el mismo argumento límite, tenemos
teniendo el mismo argumento límite, tenemos ![]() , es decir
, es decir
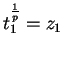 , cumpliendose esta igualdad mientras
, cumpliendose esta igualdad mientras ![]() esté en
esté en ![]() . Si ahora calculamos poco a poco:
. Si ahora calculamos poco a poco:
tomando siempre en los segundos miembros los valores de
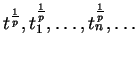 cuyos argumentos pertenecen al mismo intervalo
cuyos argumentos pertenecen al mismo intervalo
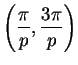 ,
tendremos también
,
tendremos también
siendo
![]() los valores seleccionados para
los valores seleccionados para
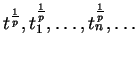 . Luego entonces los
. Luego entonces los ![]() así calculados convergen hacia el infinito en el dominio
así calculados convergen hacia el infinito en el dominio ![]() , los
, los ![]() convergen hacia el infinito en los
convergen hacia el infinito en los ![]() dominios distintos que se derivan de
dominios distintos que se derivan de ![]() por la transformación
por la transformación
![]() .
.
Podemos además llevar el punto doble a una distancia finita. Obtenemos así ![]() dominios de convergencia congregados en torno al origen teniendo cada uno como frontera una curva formada de arcos analíticos que tienen en
dominios de convergencia congregados en torno al origen teniendo cada uno como frontera una curva formada de arcos analíticos que tienen en ![]() un vértice de ángulo
un vértice de ángulo
![]() . Cada uno de estos dominios encierra en su interior los consecuentes de todos sus puntos, comprendidos los puntos frontera además del origen. En el interior de estos dominios de convergencia elementales que corresponden a
. Cada uno de estos dominios encierra en su interior los consecuentes de todos sus puntos, comprendidos los puntos frontera además del origen. En el interior de estos dominios de convergencia elementales que corresponden a ![]() , encontramos además otros que corresponden a
, encontramos además otros que corresponden a ![]() (parágrafos 8, 9, 10); estos dominios igualmente congregados en torno al origen presentan en
(parágrafos 8, 9, 10); estos dominios igualmente congregados en torno al origen presentan en ![]() un vértice2.9 de ángulo dos veces menor que
un vértice2.9 de ángulo dos veces menor que
![]() y de igual bisectriz que los precedentes; en estos dominios la convergencia de las
y de igual bisectriz que los precedentes; en estos dominios la convergencia de las ![]() es uniforme (frontera incluida). Por último, si reemplazamos
es uniforme (frontera incluida). Por último, si reemplazamos ![]() por la rama de la función inversa representada por la serie
por la rama de la función inversa representada por la serie
obtenemos un ensamblaje análogo de dominios de convergencia simple o uniforme ![]() y
y ![]() que ofrecen una disposición parecida a aquella de los dominios
que ofrecen una disposición parecida a aquella de los dominios ![]() y
y ![]() por una rotación de
por una rotación de ![]() ; las bisectrices de los ángulos en
; las bisectrices de los ángulos en ![]() de los dominios del primer ensamblaje coinciden con las tangentes en
de los dominios del primer ensamblaje coinciden con las tangentes en ![]() a las curvas límites de los dominios del segundo. Los dominios
a las curvas límites de los dominios del segundo. Los dominios ![]() de convergencia simple relativos a los consecuentes de un punto y los dominios
de convergencia simple relativos a los consecuentes de un punto y los dominios ![]() de convergencia uniforme relativos a los antecedentes tienen aún sectores comunes de ángulo en el vértice
de convergencia uniforme relativos a los antecedentes tienen aún sectores comunes de ángulo en el vértice
![]() , en total siendo
, en total siendo ![]() . Igual para los dominios
. Igual para los dominios ![]() y
y ![]() .
.
Señalemos finalmente que tendremos para las ![]() , cuando
, cuando ![]() está en un dominio
está en un dominio ![]() , una expresión asintótica de la forma
, una expresión asintótica de la forma
![\begin{displaymath}
z_n = \frac{1}{\sqrt[\textstyle p]{n\,p\,a + o(n^{1-\frac{1}{p}})}}.
\end{displaymath}](img679.png)
Damos (figura IV) una figura esquemática del conjunto de
los diversos dominios
![]() en el caso de
en el caso de ![]() . Daremos frecuentemente a este ensamblaje de dominios el nombre de estrella relativa o punto doble. Es bueno señalar a propósito de esta estrella:
. Daremos frecuentemente a este ensamblaje de dominios el nombre de estrella relativa o punto doble. Es bueno señalar a propósito de esta estrella: ![]() que los dominios que la componen son interiores a un círculo cuyo radio puede ser tomado tan pequeño como se requiera;
que los dominios que la componen son interiores a un círculo cuyo radio puede ser tomado tan pequeño como se requiera; ![]() que la forma y la naturaleza de las curvas que les limitan pueden ser variadas de una infinidad de maneras sin tener la menor importancia. Falta solamente tener en cuenta el hecho de que son simplemente conexas y la medida de los ángulos que representan en el punto
que la forma y la naturaleza de las curvas que les limitan pueden ser variadas de una infinidad de maneras sin tener la menor importancia. Falta solamente tener en cuenta el hecho de que son simplemente conexas y la medida de los ángulos que representan en el punto ![]() .
.
El análisis precedente no da una expresión asintótica de las ![]() quienes permiten demostrar la existencia de una función que satisface la ecuación de Abel. Para conseguirlo haremos preceder el empleo de la transformación conforme
quienes permiten demostrar la existencia de una función que satisface la ecuación de Abel. Para conseguirlo haremos preceder el empleo de la transformación conforme ![]() de otra transformación destinada a hacer desaparecer un cierto número de términos de
de otra transformación destinada a hacer desaparecer un cierto número de términos de ![]() . Suponiendo en el origen el punto doble, estableceremos
. Suponiendo en el origen el punto doble, estableceremos
y haremos el cambio de variables
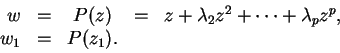
De donde extraemos las expresiones de ![]() y
y ![]() en función de
en función de ![]() y
y ![]() bajo la forma de serie entera comenzando por los términos
bajo la forma de serie entera comenzando por los términos ![]() y
y ![]() . Llevando estos valores a la ecuación
. Llevando estos valores a la ecuación ![]() , obtenemos una relación entre
, obtenemos una relación entre ![]() y
y ![]() que, resuelta con respecto a
que, resuelta con respecto a ![]() , aún será de la forma
, aún será de la forma
lo que verificamos fácilmente. Buscaremos determinar las ![]() de manera que
de manera que
![]() . Escribiremos entonces a priori
. Escribiremos entonces a priori
es decir
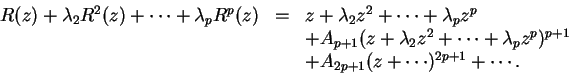
Los coeficientes de las potencias de ![]() hasta
hasta ![]() son identicos en los dos miembros; igualando los términos en
son identicos en los dos miembros; igualando los términos en ![]() , obtenemos
, obtenemos
![]() . La igualdad precedente puede entonces ser escrita
. La igualdad precedente puede entonces ser escrita
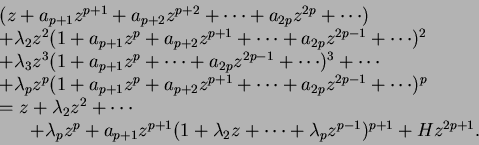
Igualando los coeficientes de
![]() en los dos miembros, obtenemos
en los dos miembros, obtenemos
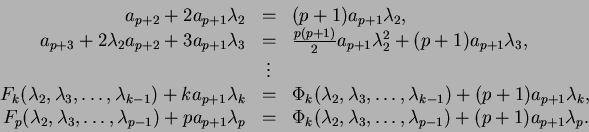
En estas ecuaciones, los ![]() y los
y los ![]() son polinomios en
son polinomios en
![]() que dependen de los coeficientes
que dependen de los coeficientes ![]() hasta
hasta ![]() a lo más. Estableciendo
a lo más. Estableciendo
![]() obtenemos de lo anterior
obtenemos de lo anterior
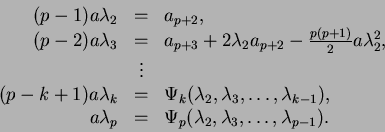
Obtenemos entonces poco a poco los valores de los coeficientes
![]() . Siendo así determinados los
. Siendo así determinados los ![]() , el cambio de la variable
, el cambio de la variable ![]() ,
, ![]() conduce bien a una relación de la forma
conduce bien a una relación de la forma
siendo convergente, el segundo miembro, en un círculo de radio no nulo, como resulta de la teoría de funciones implícitas. (Hemos cambiado el signo de ![]() para adaptarnos a las notaciones anteriormente empleadas.) Efectuamos ahora el cambio de las variables ya empleadas
para adaptarnos a las notaciones anteriormente empleadas.) Efectuamos ahora el cambio de las variables ya empleadas
![]() ,
,
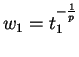 . Obtenemos
. Obtenemos
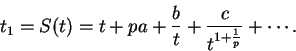
Estamos entonces en el caso donde el desarrollo de ![]() , ordenado según las potencias descendentes de
, ordenado según las potencias descendentes de ![]() , tiene por primer término un exponente negativo un término en
, tiene por primer término un exponente negativo un término en ![]() . Las consideraciones del parágrafo 10 sobre los valores asintóticos de
. Las consideraciones del parágrafo 10 sobre los valores asintóticos de ![]() y la ecuación de Abel son entonces aplicables. Si
y la ecuación de Abel son entonces aplicables. Si ![]() está en el dominio
está en el dominio ![]() , tenemos para
, tenemos para
la expresión asintótica
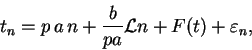
con ![]() satisfaciendo la ecuación de Abel. Si
satisfaciendo la ecuación de Abel. Si ![]() permanece en un dominio
permanece en un dominio
![]() , tenemos para grandes valores de
, tenemos para grandes valores de ![]()
A estos dominios ![]() y
y ![]() la transformación conforme
la transformación conforme
![]() hace corresponder en el plano de la variable compleja
hace corresponder en el plano de la variable compleja ![]() un ensamblaje de
un ensamblaje de ![]() dominios
dominios
![]() ;
;
![]() cuya disposición ha sido descrita anteriormente y en los cuales las funciones
cuya disposición ha sido descrita anteriormente y en los cuales las funciones ![]() , resultando de la iteración
, resultando de la iteración ![]() , convergen ya sea simplemente o uniformemente hacia cero (
, convergen ya sea simplemente o uniformemente hacia cero (![]() )2.10 Podemos además suponer a esta estrella interior al círculo de convergencia de la serie
)2.10 Podemos además suponer a esta estrella interior al círculo de convergencia de la serie
![]() para la cual hacemos la inversión de la función
para la cual hacemos la inversión de la función ![]() . A esta estrella, la transformación conforme
. A esta estrella, la transformación conforme ![]() , regular cuando
, regular cuando ![]() está en este círculo, hace corresponder una estrella presentando una distribución análoga , la transformación conserva los ángulos al igual que las direcciones en torno al origen. En los nuevos dominios así obtenidos
está en este círculo, hace corresponder una estrella presentando una distribución análoga , la transformación conserva los ángulos al igual que las direcciones en torno al origen. En los nuevos dominios así obtenidos
![]() ;
;
![]() ; los
; los ![]() convergen ya sea simplemente o uniformemente hacia cero. Señalemos de paso que esta estrella no es necesariamente idéntica a aquella que hubieramos obtenido por el procedimiento del parágrafo 11, sin hacer uso de la transformación auxiliar
convergen ya sea simplemente o uniformemente hacia cero. Señalemos de paso que esta estrella no es necesariamente idéntica a aquella que hubieramos obtenido por el procedimiento del parágrafo 11, sin hacer uso de la transformación auxiliar ![]() . Sea lo que fuere, tendremos en el dominio
. Sea lo que fuere, tendremos en el dominio ![]() por ejemplo una expresión asintótica que se obtiene eliminando las variables auxiliares entre las ecuaciones
por ejemplo una expresión asintótica que se obtiene eliminando las variables auxiliares entre las ecuaciones
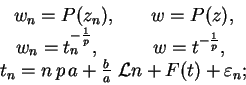
de donde
![\begin{displaymath}
P(z_n) = \frac{1}{\sqrt[p]{npa + \frac{b}{a} {\cal L}n + f(z) + \varepsilon_n}},
\end{displaymath}](img732.png)
con
![\begin{displaymath}
\begin{array}{c}
f(z) = F\left[ \frac{1}{P^p(z)} \right], \\
f[R(z)] = f(z) + pa.
\end{array}\end{displaymath}](img733.png)
A propósito de estas fórmulas, son necesarias diversas observaciones:
![]() Para obtener la expresión asintótica explícita de
Para obtener la expresión asintótica explícita de ![]() , hay que resolver la ecuación
, hay que resolver la ecuación ![]() con respecto a
con respecto a ![]() a través de la serie convergente
a través de la serie convergente
y reemplazar ![]() por
por
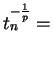
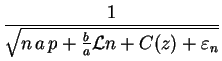 . Podemos conservar solamente los
. Podemos conservar solamente los ![]() primeros términos del desarrollo. En efecto, con
primeros términos del desarrollo. En efecto, con ![]() infinitamente pequeño cuyo orden de trabajo nos es desconocido, el primer término
infinitamente pequeño cuyo orden de trabajo nos es desconocido, el primer término ![]() no es conocido más que en una cantidad cerca del orden de
no es conocido más que en una cantidad cerca del orden de
 o de
o de
![]() , es decir de un orden inferior al de
, es decir de un orden inferior al de ![]() , pero además desconocido. Es entonces inútil escribir los términos en
, pero además desconocido. Es entonces inútil escribir los términos en
![]() .
.
![]() Recordemos que
Recordemos que ![]() es el coeficiente, con signo contrario, de
es el coeficiente, con signo contrario, de ![]() en el desarrollo de
en el desarrollo de ![]() ; los coeficientes
; los coeficientes ![]() y
y ![]() , por otra parte son funciones racionales de los coeficientes de
, por otra parte son funciones racionales de los coeficientes de ![]() hasta el término en
hasta el término en ![]() .
.
![]() La elección de los radicales en estas fórmulas depende de aquella de los dominios
La elección de los radicales en estas fórmulas depende de aquella de los dominios ![]() . Señalemos además que la función de Abel
. Señalemos además que la función de Abel ![]() en el plano de la variable
en el plano de la variable ![]() no es en general la misma para las determinaciones de
no es en general la misma para las determinaciones de ![]() ; será la misma en el caso particular donde
; será la misma en el caso particular donde ![]() no contenga términos en exponente fraccionario, es decir si
no contenga términos en exponente fraccionario, es decir si ![]() no contiene más que términos en
no contiene más que términos en ![]() . Las
. Las ![]() funciones de Abel
funciones de Abel ![]() , relativas a la substitución
, relativas a la substitución
![]() y deducidas de
y deducidas de ![]() por la fórmula
por la fórmula
![]() , están definidas y son holomorfas en los
, están definidas y son holomorfas en los ![]() dominios
dominios ![]() respectivamente. En los dominios
respectivamente. En los dominios ![]() satisfacen la condición asintótica
satisfacen la condición asintótica
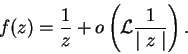
Demostraremos fácilmente que los dominios ![]() pueden ser elegidos de manera que no tomen más que una sola vez cada valor, y extenderemos fácilmente las propiedades demostradas en el parágrafo 9 refiriendo las curvas invariantes y la iteración analítica . Veremos por ejemplo que los consecuentes de un punto del dominio
pueden ser elegidos de manera que no tomen más que una sola vez cada valor, y extenderemos fácilmente las propiedades demostradas en el parágrafo 9 refiriendo las curvas invariantes y la iteración analítica . Veremos por ejemplo que los consecuentes de un punto del dominio ![]() están repartidos sobre una curva invariante teniendo por tangente en
están repartidos sobre una curva invariante teniendo por tangente en ![]() la bisectriz del ángulo formado por el contorno de
la bisectriz del ángulo formado por el contorno de ![]() en ese punto.
en ese punto.
Ejemplo:
![]() . | El punto en el infinito es un punto doble de multiplicador igual a
. | El punto en el infinito es un punto doble de multiplicador igual a ![]() para el cual el entero
para el cual el entero ![]() . Verificaremos que
. Verificaremos que ![]() converge uniformemente hacia el infinito en todo dominio acotado no conteniendo ningún punto del eje de las cantidades imaginarias. En cada uno de los dos semiplanos
converge uniformemente hacia el infinito en todo dominio acotado no conteniendo ningún punto del eje de las cantidades imaginarias. En cada uno de los dos semiplanos ![]() y
y ![]() tenemos
tenemos
con ![]() satisfaciendo la ecuación de Abel
satisfaciendo la ecuación de Abel
![]() es holomorfa tanto a la derecha como a la izquierda del eje imaginario. Mostraremos que esta recta es una línea singular esencial de
es holomorfa tanto a la derecha como a la izquierda del eje imaginario. Mostraremos que esta recta es una línea singular esencial de ![]() , a lo que regresaremos posteriormente.
, a lo que regresaremos posteriormente.
Así, dado un punto doble de multiplicador ![]() , hemos aprendido a encontrar regiones del plano para las cuales este punto es un punto frontera y en las cuales hay convergencia de los consecuentes desde un punto cualquiera hacia este punto doble. Debemos preguntarnos ahora si los puntos así obtenidos, agregando sus antecedentes, son los únicos puntos para los cuales
, hemos aprendido a encontrar regiones del plano para las cuales este punto es un punto frontera y en las cuales hay convergencia de los consecuentes desde un punto cualquiera hacia este punto doble. Debemos preguntarnos ahora si los puntos así obtenidos, agregando sus antecedentes, son los únicos puntos para los cuales ![]() convergen hacia el punto doble. Estando siempre, el punto doble, confinado en el infinito,
convergen hacia el punto doble. Estando siempre, el punto doble, confinado en el infinito,
y ![]() un punto cuyos consecuentes tienden hacia el infinito; estando los
un punto cuyos consecuentes tienden hacia el infinito; estando los ![]() a partir de un cierto rango en el dominio de convergencia en la serie que precede, podemos suponer que así sucede a partir de la misma
a partir de un cierto rango en el dominio de convergencia en la serie que precede, podemos suponer que así sucede a partir de la misma ![]() . Si establecemos
. Si establecemos
![]() , tenemos
, tenemos
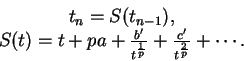
La parte infinitamente pequeña de ![]() tiene en general determinaciones multiples, pero no tendremos necesidad de saber de que manera hay que elegir las determinaciones de los radicales. Nos basta señalar que se puede asumir a
tiene en general determinaciones multiples, pero no tendremos necesidad de saber de que manera hay que elegir las determinaciones de los radicales. Nos basta señalar que se puede asumir a
![]() más pequeña, en módulo, que
más pequeña, en módulo, que
![]() cuando reemplazamos
cuando reemplazamos ![]() por
por
![]() .
.
Tendremos entonces
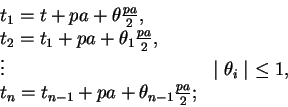
de donde
o, tomando la parte real de los dos miembros,
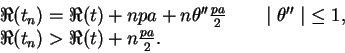
esta última expresión es infinita positiva al mismo tiempo que ![]() . Si entonces los puntos
. Si entonces los puntos ![]() no coinciden jamás con el punto en el infinito, permanecen a partir de un cierto rango, en sentido estricto interiores al dominio
no coinciden jamás con el punto en el infinito, permanecen a partir de un cierto rango, en sentido estricto interiores al dominio ![]() al igual que al dominio
al igual que al dominio ![]() ; podemos agregar que el argumento de
; podemos agregar que el argumento de ![]() tiende a cero. Los puntos
tiende a cero. Los puntos ![]() serán entonces a partir de un cierto rango constantemente interiores a uno de los
serán entonces a partir de un cierto rango constantemente interiores a uno de los ![]() dominios
dominios ![]() que se deducen por la transformación conforme
que se deducen por la transformación conforme ![]() ; que será naturalmente siempre el mismo dominio
; que será naturalmente siempre el mismo dominio ![]() . Los puntos buscados son entonces, por una parte, los antecedentes del punto doble; y por otra, los puntos interiores en sentido estricto a los dominios
. Los puntos buscados son entonces, por una parte, los antecedentes del punto doble; y por otra, los puntos interiores en sentido estricto a los dominios ![]() o
o ![]() y sus antecedentes. Los puntos de la segunda categoría son cada uno el centro de un dominio en el cual hay convergencia uniforme puesto que hay convergencia unifome en los dominios cerrados
y sus antecedentes. Los puntos de la segunda categoría son cada uno el centro de un dominio en el cual hay convergencia uniforme puesto que hay convergencia unifome en los dominios cerrados ![]() . Los puntos de la categoría, es decir los antecedentes del punto doble que son una infinidad numerable (asumiremos para mayor claridad que
. Los puntos de la categoría, es decir los antecedentes del punto doble que son una infinidad numerable (asumiremos para mayor claridad que ![]() es racional) no gozan de esta propiedad. Vamos a mostrar en efecto que los
es racional) no gozan de esta propiedad. Vamos a mostrar en efecto que los ![]() no pueden formar una serie uniformemente convergente en un dominio que comprende el punto doble en su interior. Esta vez supongamos que el punto doble está en el origen. En el círculo de centro
no pueden formar una serie uniformemente convergente en un dominio que comprende el punto doble en su interior. Esta vez supongamos que el punto doble está en el origen. En el círculo de centro ![]() , hay regiones donde las funciones
, hay regiones donde las funciones ![]() convergen uniformemente hacia cero. Sea
convergen uniformemente hacia cero. Sea ![]() un punto interior a una de estas regiones. En un círculo
un punto interior a una de estas regiones. En un círculo ![]() de centro
de centro ![]() y de radio
y de radio ![]() arbitrario, existen entonces puntos
arbitrario, existen entonces puntos ![]() para los cuales
para los cuales
cualquiera que sea el entero ![]() , las funciones
, las funciones ![]() no pueden entonces converger uniformemente hacia cero en
no pueden entonces converger uniformemente hacia cero en ![]() . Pero existen también regiones de
. Pero existen también regiones de ![]() donde las
donde las ![]() convergen uniformemente hacia la constante cero. De lo que se deduce que las
convergen uniformemente hacia la constante cero. De lo que se deduce que las ![]() no convergen uniformemente en todo el círculo
no convergen uniformemente en todo el círculo ![]() .
.
Podemos demostrar la misma proposición de una manera más directa y más instructiva. Para mayor claridad siempre se asume a ![]() racional, decimos que en el círculo
racional, decimos que en el círculo ![]() de centro
de centro ![]() y de radio
y de radio ![]() arbitrario, las
arbitrario, las ![]() no pueden ser formadas uniformemente. Pues si lo fueran, serían holomorfas en
no pueden ser formadas uniformemente. Pues si lo fueran, serían holomorfas en ![]() cualquiera que sea
cualquiera que sea ![]() ; tendríamos entonces en
; tendríamos entonces en ![]() el desarrollo convergente (
el desarrollo convergente (![]() 3)
3)
Sea ![]() el módulo máximo de
el módulo máximo de ![]() sobre la circunferencia de centro
sobre la circunferencia de centro ![]() y de radio
y de radio ![]() . Tenemos
. Tenemos
El segundo miembro llega a ser infinito con ![]() . Entonces, en el círculo
. Entonces, en el círculo ![]() , o bien las funciones
, o bien las funciones ![]() tienen polos, o bien toman valores infinitamente grandes con
tienen polos, o bien toman valores infinitamente grandes con ![]() . Por otra parte, siempre tenemos
. Por otra parte, siempre tenemos ![]() . Entonces en un círculo cualquiera de centro
. Entonces en un círculo cualquiera de centro ![]() los
los ![]() y, más generalmente, una serie cualquiera extraída de las
y, más generalmente, una serie cualquiera extraída de las ![]() no pueden converger uniformemente.
no pueden converger uniformemente.
Sucederá lo mismo para todo dominio en torno a un antecedente del punto doble. Sabemos de antemano que en ciertos dominios cerrados simplemente conexos que tienen el punto doble (o uno de sus antecedentes) sobre su frontera, hay convergencia uniforme.
Ahora vamos a estudiar lo que sucede alrededor de un punto doble cuyo multiplicador tiene por módulo la unidad con un argumento *conmensurable* a ![]() . Sea entonces
. Sea entonces
donde
![]() , siendo
, siendo ![]() y
y ![]() enteros primos entre sí. Tendremos
enteros primos entre sí. Tendremos
y en particular
Suponemos ![]() , es decir que
, es decir que ![]() es el primer término no nulo que sigue al término en
es el primer término no nulo que sigue al término en ![]() ; dejamos entonces de lado por el momento el caso particular donde
; dejamos entonces de lado por el momento el caso particular donde ![]() sería igual a
sería igual a ![]() . Decimos que
. Decimos que ![]() es de la forma
es de la forma ![]() . En efecto, en virtud de la identidad
. En efecto, en virtud de la identidad
tendremos
![\begin{displaymath}
\begin{array}{l}
(sz + a_2z^2 + \cdots + a_hz^h + \cdots)
+...
...z^h + \cdots]^2 + a_h[z + \cdots]^h \\
+ Kz^{h+1},
\end{array}\end{displaymath}](img793.png)
siendo ![]() y
y ![]() series enteras. Igualando los términos en
series enteras. Igualando los términos en ![]() , tenemos
, tenemos
de donde
Como ![]() , tenemos entonces
, tenemos entonces ![]() , y como
, y como ![]() es raíz primitiva de
es raíz primitiva de ![]() ,
, ![]() es múltiplo de
es múltiplo de ![]() o
o ![]() .
.
Dado lo anterior, la transformación
![]() es, en un dominio suficientemente pequeño alrededor del origen, una transformación conforme sin puntos singulares que equivalen para
es, en un dominio suficientemente pequeño alrededor del origen, una transformación conforme sin puntos singulares que equivalen para ![]() infinitamente pequeño a una rotación del ángulo
infinitamente pequeño a una rotación del ángulo ![]() alrededor del origen. Por otra parte sabemos que las funciones iteradas de
alrededor del origen. Por otra parte sabemos que las funciones iteradas de ![]() convergen hacia cero en
convergen hacia cero en ![]() dominios congregados en torno de
dominios congregados en torno de ![]() y forman una estrella; estos dominios tienen en
y forman una estrella; estos dominios tienen en ![]() un extremo del ángulo
un extremo del ángulo
![]() . Consideramos a
. Consideramos a ![]() de estos dominios encontrados sucesivamente sobre una circunferencia infinitamente pequeña de centro
de estos dominios encontrados sucesivamente sobre una circunferencia infinitamente pequeña de centro ![]() y congregados en un sector de ángulo
y congregados en un sector de ángulo
![]() . Sean
. Sean
![]() , estos
, estos ![]() dominios que vamos a transformar sucesivamente por
dominios que vamos a transformar sucesivamente por
![]() . Obtenemos así
. Obtenemos así ![]() dominios que son designados por la Tabla siguiente
dominios que son designados por la Tabla siguiente
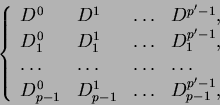
Se puede asumir que estos dominio son interiores al círculo
![]() , siendo las funciones
, siendo las funciones ![]() hasta
hasta ![]() , todas regulares y no tomando más que una sola vez cada valor en este círculo. Se sigue que los dominios de esta Tabla son dominios simples que no se translapan a sí mismos. Están por otra parte congregados en torno de
, todas regulares y no tomando más que una sola vez cada valor en este círculo. Se sigue que los dominios de esta Tabla son dominios simples que no se translapan a sí mismos. Están por otra parte congregados en torno de ![]() y todos presentan en
y todos presentan en ![]() un extremo de ángulo
un extremo de ángulo
![]() , las tangentes a estos puntos en
, las tangentes a estos puntos en ![]() forman un haz isogonal cuyos ángulos recubren sin doble empleo un intervalo igual a
forman un haz isogonal cuyos ángulos recubren sin doble empleo un intervalo igual a ![]() . Decimos además que estos
. Decimos además que estos ![]() dominios no tienen punto en común.
dominios no tienen punto en común.
En efecto, sea ![]() un punto que pertenece a un dominio inscrito en la primera línea
un punto que pertenece a un dominio inscrito en la primera línea ![]() . Sabemos que
. Sabemos que ![]() tiende a cero y que su argumento tiene por límite el ángulo
tiende a cero y que su argumento tiene por límite el ángulo ![]() de
de ![]() con la bisectriz del extremo del dominio
con la bisectriz del extremo del dominio ![]() en punto
en punto ![]() ; para
; para ![]() ,
, ![]() no siendo necesariamente múltiplo de
no siendo necesariamente múltiplo de ![]() , este argumento tendrá por valor límite
, este argumento tendrá por valor límite ![]()
![]() ; la misma propiedad subsiste para todos los dominios de la Tabla; de lo que se deduce fácilmente que dos puntos perteneciendo a dos dominios diferentes tienen sus consecuentes distintos a partir de un cierto rango. Estos dos dominios no tienen entonces puntos comunes y coinciden solamente en
; la misma propiedad subsiste para todos los dominios de la Tabla; de lo que se deduce fácilmente que dos puntos perteneciendo a dos dominios diferentes tienen sus consecuentes distintos a partir de un cierto rango. Estos dos dominios no tienen entonces puntos comunes y coinciden solamente en ![]() . Los dominios de la tabla forman entonces un ensamblaje estrella de igual estructura que la estrella considerada al inicio. Los dominios de una misma columna forman un ciclo, los consecuentes sucesivos de un punto de uno de estos dominios siendo periódicamente interiores a los
. Los dominios de la tabla forman entonces un ensamblaje estrella de igual estructura que la estrella considerada al inicio. Los dominios de una misma columna forman un ciclo, los consecuentes sucesivos de un punto de uno de estos dominios siendo periódicamente interiores a los ![]() dominios del ciclo. Al contrario, dos dominios perteneciendo a dos columnas distintas están formados de puntos que nunca son iguales para las potencias de la substitución
dominios del ciclo. Al contrario, dos dominios perteneciendo a dos columnas distintas están formados de puntos que nunca son iguales para las potencias de la substitución
![]() .
.
Finalmente, todos los puntos del plano cuyos consecuentes tienden hacia el origen son antecedentes de los puntos interiores a los dominios de la Tabla, o del origen mismo. Dejaremos de lado las extensiones fáciles de las propiedades demostradas en los parágrafos anteriores refiriendo los valores asintóticos de ![]() y la ecuación de Abel. Demostramos además muy fácilmente que ni las
y la ecuación de Abel. Demostramos además muy fácilmente que ni las ![]() , ni ninguna de las series infinitas que podemos extraer, converge uniformemente en un círculo de centro
, ni ninguna de las series infinitas que podemos extraer, converge uniformemente en un círculo de centro ![]() . Pues si existiera tal serie, podríamos extraer otra donde todos los enteros
. Pues si existiera tal serie, podríamos extraer otra donde todos los enteros ![]() serían congruentes entre ellos
serían congruentes entre ellos ![]() y de la forma
y de la forma ![]() ; las funciones
; las funciones
![]() convergiendo uniformemente en un círculo de centro
convergiendo uniformemente en un círculo de centro ![]() , y sería lo mismo para las funciones
, y sería lo mismo para las funciones
![]() que son las iteradas de una función de multiplicador
que son las iteradas de una función de multiplicador ![]() en el punto doble
en el punto doble ![]() . Entonces somos llevados a una cuestión ya resuelta. Señalemos también que podríamos completar la estrella obtenida por un conjunto análogo de dominios relativos a los antecedentes de un punto.
. Entonces somos llevados a una cuestión ya resuelta. Señalemos también que podríamos completar la estrella obtenida por un conjunto análogo de dominios relativos a los antecedentes de un punto.
Hemos dejado de lado el caso donde ![]() es idéntica a
es idéntica a ![]() . Si es así, las funciones
. Si es así, las funciones ![]() son periódicamente iguales a las funciones
son periódicamente iguales a las funciones
![]()
![]() y entonces no convergen a cero. Esta circunstancia se presenta para las substituciones de primer grado
y entonces no convergen a cero. Esta circunstancia se presenta para las substituciones de primer grado ![]()
![]() , y para aquellas que deducimos por la misma transformación conforme,
, y para aquellas que deducimos por la misma transformación conforme,
![]() , con
, con ![]() holomorfa y nula, pero de derivada no nula para
holomorfa y nula, pero de derivada no nula para ![]() . La relación
. La relación ![]() da entonces
da entonces
esta última ecuación será de la forma ![]() solamente si
solamente si ![]() ; desechemos esta hipótesis; tendremos entonces una substitución
; desechemos esta hipótesis; tendremos entonces una substitución ![]() , donde
, donde ![]() no es de primer grado, cuya iteración indefinida conduce solamente a
no es de primer grado, cuya iteración indefinida conduce solamente a ![]() substituciones distintas. Por ejemplo para
substituciones distintas. Por ejemplo para ![]() , podremos tomar
, podremos tomar ![]() , con la determinación del logaritmo nulo para
, con la determinación del logaritmo nulo para ![]() . Además esta circunstancia no puede presentarse si
. Además esta circunstancia no puede presentarse si ![]() es una fracción racional de grado superior a
es una fracción racional de grado superior a ![]() , o una función uniforme teniendo puntos singulares esenciales aislados, pues la inversa de dicha función jamás es uniforme según los teoremas de Picard.
, o una función uniforme teniendo puntos singulares esenciales aislados, pues la inversa de dicha función jamás es uniforme según los teoremas de Picard.
Consideremos ahora el caso de un punto periódico cuyo multiplicador es de la forma
![]() ; si
; si ![]() es el periodo, seremos llevados al caso precedente que considera la substitución
es el periodo, seremos llevados al caso precedente que considera la substitución
![]() . Obtendremos así alrededor de los
. Obtendremos así alrededor de los ![]() puntos del ciclo
puntos del ciclo ![]() ensamblajes de dominios o estrellas en las cuales las
ensamblajes de dominios o estrellas en las cuales las ![]() convergen periódicamente hacia los puntos del ciclo; si
convergen periódicamente hacia los puntos del ciclo; si ![]() pertenece a uno de estos dominios, el punto
pertenece a uno de estos dominios, el punto ![]() pertenecerá a la misma estrella pero a un dominio diferente si
pertenecerá a la misma estrella pero a un dominio diferente si ![]() ; el punto
; el punto ![]() pertenecerá al mismo dominio que
pertenecerá al mismo dominio que ![]() ; los puntos
; los puntos
![]() tienden hacia el punto doble correspondiente sin salir de este dominio; de cualquier manera hay una doble periodicidad, una de posición la otra de orientación. Los dominios de las
tienden hacia el punto doble correspondiente sin salir de este dominio; de cualquier manera hay una doble periodicidad, una de posición la otra de orientación. Los dominios de las ![]() estrellas forman así
estrellas forman así ![]() grupos o ciclos
grupos o ciclos ![]() ; dos puntos que pertenecen a dominios de dos ciclos distintos jamás son iguales para las potencias de la substitución dada.
; dos puntos que pertenecen a dominios de dos ciclos distintos jamás son iguales para las potencias de la substitución dada.
Resta estudiar los puntos dobles cuyo multiplicador es de la forma ![]() , siendo
, siendo ![]() un número inconmensurable a
un número inconmensurable a ![]() . Conocemos muy poco sobre estos puntos dobles, cuyo estudio desde el punto de vista que nos ocupa parece muy dificil. Consideremos primero una substitución de primer grado
. Conocemos muy poco sobre estos puntos dobles, cuyo estudio desde el punto de vista que nos ocupa parece muy dificil. Consideremos primero una substitución de primer grado
![]() ; la iteración da
; la iteración da
![]() ; los puntos
; los puntos ![]() están distribuidos de una manera densa sobre toda la circunferencia de centro
están distribuidos de una manera densa sobre toda la circunferencia de centro ![]() pasando por
pasando por ![]() y la serie de las funciones
y la serie de las funciones ![]() admite como funciones límite todas las funciones
admite como funciones límite todas las funciones ![]() , donde
, donde ![]() es un número real cualquiera. Si establecemos como anteriormente
es un número real cualquiera. Si establecemos como anteriormente
![]() con
con
![]() , obtenemos una nueva substitución
, obtenemos una nueva substitución ![]() con
con
![]() , que en general no es de primer grado y es tal, que los consecuentes de un punto están distribuidos de una manera densa sobre una curva cerrada analítica en torno al punto doble. Entonces en la vecindad del punto doble, los consecuentes de un punto (además del punto doble) no tienden jamás a ese punto. Pero dada la subtitución
, que en general no es de primer grado y es tal, que los consecuentes de un punto están distribuidos de una manera densa sobre una curva cerrada analítica en torno al punto doble. Entonces en la vecindad del punto doble, los consecuentes de un punto (además del punto doble) no tienden jamás a ese punto. Pero dada la subtitución
![]() , no es fácil ver si cae en la categoría anterior. Supongamos que no sea así: ¿existen entonces dominios cuyos consecuentes tienden hacia el punto doble? En este momento no podemos ni dar un ejemplo, ni probar que el hecho sea imposible2.11.
, no es fácil ver si cae en la categoría anterior. Supongamos que no sea así: ¿existen entonces dominios cuyos consecuentes tienden hacia el punto doble? En este momento no podemos ni dar un ejemplo, ni probar que el hecho sea imposible2.11.
Ahora solamente vamos a estudiar los puntos dobles repulsores cuyo multiplicador es más grande que ![]() , en módulo. Si
, en módulo. Si ![]() es un punto de esta especie, existe un número real
es un punto de esta especie, existe un número real ![]() comprendido entre
comprendido entre ![]() y
y
![]() , tal que para todo punto
, tal que para todo punto ![]() interior al círculo
interior al círculo
![]() , tendríamos
, tendríamos
Si los puntos
![]() son todos interiores a este mismo círculo, tendremos también
son todos interiores a este mismo círculo, tendremos también
![]() , cantidad que crece infinitamente con
, cantidad que crece infinitamente con ![]() ; los puntos
; los puntos ![]() terminan entonces por salir del círculo. Es claro que aparte del mismo punto doble, los consecuentes de un punto del círculo jamás tienden hacia el punto doble. Si
terminan entonces por salir del círculo. Es claro que aparte del mismo punto doble, los consecuentes de un punto del círculo jamás tienden hacia el punto doble. Si ![]() está definido y es uniforme en todo el plano y también racional para fijar las ideas, tendremos sobre una circunferencia de centro
está definido y es uniforme en todo el plano y también racional para fijar las ideas, tendremos sobre una circunferencia de centro ![]() y de radio
y de radio ![]()
con ![]() designando el módulo máximo de
designando el módulo máximo de ![]() que se asume holomorfa para
que se asume holomorfa para
![]() . Si esta última ecuación no es satisfecha,
. Si esta última ecuación no es satisfecha, ![]() tiene al menos un polo sobre la circunferencia o en el interior. Por consecuencia, en todo círculo de centro
tiene al menos un polo sobre la circunferencia o en el interior. Por consecuencia, en todo círculo de centro ![]() ,
, ![]() toma valores de módulo indefinidamente creciente con
toma valores de módulo indefinidamente creciente con ![]() . Como, por otra parte, siempre tenemos
. Como, por otra parte, siempre tenemos
![]() , ninguna serie infinita extraída de los
, ninguna serie infinita extraída de los ![]() puede converger uniformemente en un círculo de centro
puede converger uniformemente en un círculo de centro ![]() .
.
La función inversa de ![]() , igual a
, igual a ![]() para
para ![]() , es desarrollable para
, es desarrollable para
![]() suficientemente pequeño en serie entera:
suficientemente pequeño en serie entera:
El punto doble ![]() es entonces un punto doble atractor de multiplicador
es entonces un punto doble atractor de multiplicador
![]() para la substitución
para la substitución
![]() . Entonces, en cierto dominio del punto
. Entonces, en cierto dominio del punto ![]() , los antecedentes de
, los antecedentes de ![]() obtenidos a través de la rama de la función
obtenidos a través de la rama de la función ![]() que acabamos de definir convergen uniformemente hacia
que acabamos de definir convergen uniformemente hacia ![]() . Existe una función holomorfa y nula en
. Existe una función holomorfa y nula en ![]() , de derivada igual a
, de derivada igual a ![]() en el punto que verifica la ecuación funcional de Schröder
en el punto que verifica la ecuación funcional de Schröder
de donde
La función inversa de ![]() ,
, ![]() igual a
igual a ![]() para
para ![]() y holomorfa en este punto verifica la ecuación funcional
y holomorfa en este punto verifica la ecuación funcional
Ahora vamos a demostrar un teorema referente al conjunto ![]() 2.12 obtenido de los consecuentes de un punto, suponiendo siempre para evitar confusión
2.12 obtenido de los consecuentes de un punto, suponiendo siempre para evitar confusión ![]() racional. Supongamos que este conjunto contiene el punto doble
racional. Supongamos que este conjunto contiene el punto doble ![]() de multiplicador
de multiplicador ![]() tal que
tal que
![]() . Si este conjunto encierra otros puntos además de
. Si este conjunto encierra otros puntos además de ![]() (que es ciertamente el caso, como acabamos de ver, cuando
(que es ciertamente el caso, como acabamos de ver, cuando
![]() y cuando
y cuando ![]() no es un antecedente de
no es un antecedente de ![]() ), encierra una infinidad que tiene a
), encierra una infinidad que tiene a ![]() por punto límite. En efecto, no siendo
por punto límite. En efecto, no siendo ![]() un antecedente de
un antecedente de ![]() tendrá todos sus consecuentes distintos, sino
tendrá todos sus consecuentes distintos, sino ![]() sería el antecedente de un punto periódico que coincidiría necesariamente con
sería el antecedente de un punto periódico que coincidiría necesariamente con ![]() , ya que
, ya que ![]() es un punto invariante y límite de ciertos consecuentes de
es un punto invariante y límite de ciertos consecuentes de ![]() . Sentado lo anterior, tendremos, en un círculo de centro
. Sentado lo anterior, tendremos, en un círculo de centro ![]() y de radio
y de radio ![]() ,
,
siendo ![]() un número finito pero más grande que
un número finito pero más grande que ![]() ;
; ![]() debe ser asumido suficientemente pequeño para que exista en el exterior del círculo un punto límite
debe ser asumido suficientemente pequeño para que exista en el exterior del círculo un punto límite ![]() de los
de los ![]() , lo que es posible ya que
, lo que es posible ya que ![]() no es el único punto límite. Siendo
no es el único punto límite. Siendo ![]() un número comprendido entre
un número comprendido entre ![]() y
y
![]() , y
, y ![]() un consecuente de
un consecuente de ![]() tal que
tal que
![]() ; puesto que los
; puesto que los ![]() tienen a
tienen a ![]() entre sus puntos límite, hay consecuentes de
entre sus puntos límite, hay consecuentes de ![]() cuya distancia a
cuya distancia a ![]() es superior a
es superior a ![]() . Sea
. Sea
![]() el primer consecuente de
el primer consecuente de ![]() para el cual
para el cual
![]() ; como
; como
![]() , tendremos
, tendremos
![]() . El punto
. El punto
![]() es entonces interior a la corona
es entonces interior a la corona ![]() . Sea
. Sea ![]() , el primer consecuente de
, el primer consecuente de ![]() después
después
![]() para el cual
para el cual
![]() ;
; ![]() existe ya que
existe ya que ![]() es punto límite de los
es punto límite de los ![]() . Deduciremos como antes la existencia de
. Deduciremos como antes la existencia de
![]() comprendidos en la corona
comprendidos en la corona ![]() . Obtenemos así la serie de puntos
. Obtenemos así la serie de puntos
![]() cuyos índices van creciendo, que son entonces todos distintos y todos interiores a la corona
cuyos índices van creciendo, que son entonces todos distintos y todos interiores a la corona ![]() . Tienen entonces al menos un punto límite en esta corona o sobre su contorno. Haciendo sucesivamente
. Tienen entonces al menos un punto límite en esta corona o sobre su contorno. Haciendo sucesivamente ![]()
 , obtenemos una serie de coronas que tienden hacia el punto
, obtenemos una serie de coronas que tienden hacia el punto ![]() y que todas contienen al menos un punto límite de las
y que todas contienen al menos un punto límite de las ![]() . El conjunto
. El conjunto ![]() contiene entonces al menos un punto.
contiene entonces al menos un punto.
Vamos a dar, para terminar, algunos ejemplos de las diversas suertes de los puntos dobles que hemos estudiado en este capítulo.
Tomemos
![]() . Hay un punto doble atractor, que es el punto doble en el infinito y dos puntos dobles repulsores que son los puntos
. Hay un punto doble atractor, que es el punto doble en el infinito y dos puntos dobles repulsores que son los puntos
![]()
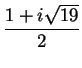 y
y ![]()
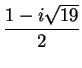 , cuyos multiplicadores son respectivamente
, cuyos multiplicadores son respectivamente ![]() y
y ![]() . Los
. Los ![]() convergen hacia el infinito para
convergen hacia el infinito para
![]() . En efecto, si
. En efecto, si
![]() tenemos
tenemos
Tenemos entonces
![]() para
para
![]() . Estudiaremos más tarde este ejemplo de una manera más concreta.
. Estudiaremos más tarde este ejemplo de una manera más concreta.
Tomamos en seguida
![]() . Tenemos siempre el punto atractor
. Tenemos siempre el punto atractor ![]() , y los dos puntos dobles repulsores
, y los dos puntos dobles repulsores ![]()
 , de multiplicador
, de multiplicador
![]() . Encontramos enseguida un ciclo de orden 2 correspondiendo a los puntos raíces
. Encontramos enseguida un ciclo de orden 2 correspondiendo a los puntos raíces ![]() y
y ![]() , la ecuación
, la ecuación
y cuyo multiplicador es igual a
![]() . La estrella del punto
. La estrella del punto ![]()
 se compone de dos dominios
se compone de dos dominios ![]() colocados a uno y otro lado de la paralela al eje imaginario conducido por
colocados a uno y otro lado de la paralela al eje imaginario conducido por ![]() y cuyos contornos son tangentes a esta recta; la estrella del punto
y cuyos contornos son tangentes a esta recta; la estrella del punto ![]()
 se compone de los dominios
se compone de los dominios ![]() ofreciendo una disposición análoga . Los consecuentes de un punto
ofreciendo una disposición análoga . Los consecuentes de un punto ![]() de
de ![]() son los puntos
son los puntos ![]() interiores a
interiores a ![]() ,
, ![]() exteriores a
exteriores a ![]() ,
, ![]() interiores a
interiores a ![]() y
y ![]() a
a ![]() . Tienden hacia
. Tienden hacia ![]() o hacia
o hacia ![]() permaneciendo sobre curvas tangentes al eje real (figura V).
permaneciendo sobre curvas tangentes al eje real (figura V).
Por último consideremos el ejemplo un poco más general
![]() . Los puntos periódicos de orden
. Los puntos periódicos de orden ![]() , siendo
, siendo ![]() primo, son los puntos raíces de la ecuación
primo, son los puntos raíces de la ecuación
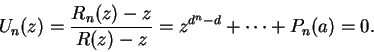
![]() es un polinomio en
es un polinomio en ![]() , que tienen como primer término a
, que tienen como primer término a ![]() y como último término la unidad. Los puntos raíces de la ecuación precedente se distribuyen en
y como último término la unidad. Los puntos raíces de la ecuación precedente se distribuyen en
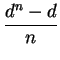 ciclos de orden
ciclos de orden ![]() .
.
Sea
![]() uno de estos ciclos. Su multiplicador será
uno de estos ciclos. Su multiplicador será
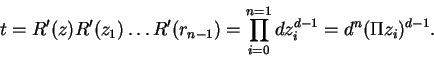
El producto de los multiplicadores de los diferentes ciclos en número
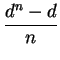 será entonces
será entonces
el producto ![]() siendo extendido a todas las raíces de
siendo extendido a todas las raíces de ![]() es decir
es decir
Si ![]() es arbitrario, podemos disponer de manera que esta expresión tome el valor que queramos. Si este valor es más pequeño que
es arbitrario, podemos disponer de manera que esta expresión tome el valor que queramos. Si este valor es más pequeño que ![]() , en módulo, habrá al menos un
, en módulo, habrá al menos un ![]() , entonces al menos un ciclo atractor de orden
, entonces al menos un ciclo atractor de orden ![]() .
.