La cubierta abierta de un espacio topológico
![]() es una familia de conjuntos abiertos cuya unión es el mismo espacio
es una familia de conjuntos abiertos cuya unión es el mismo espacio
![]() . Un espacio toplógico
. Un espacio toplógico
![]() se dirá compacto si cada cubierta abierta de éste tiene una subcubierta finita. Esto significa que
se dirá compacto si cada cubierta abierta de éste tiene una subcubierta finita. Esto significa que
![]() es compacto si cumple con lo siguiente.
es compacto si cumple con lo siguiente.
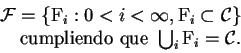 |
(18) |
En el caso del espacio de configuraciones
![]() de un autómata celular lineal, tomemos el siguiente cilindro:
de un autómata celular lineal, tomemos el siguiente cilindro:
Es decir, ![]() indexará al conjunto de cilindros donde cada cilindro cumple con que
indexará al conjunto de cilindros donde cada cilindro cumple con que
![]() donde
donde ![]() . Entonces,
. Entonces,
![]() pues
pues ![]() es un conjunto finito de estados, por lo que:
es un conjunto finito de estados, por lo que:
![$\displaystyle \mathcal{F}=\bigcup_i \mathfrak{C}_{0}({\mathrm{C}_{i[0]}}) = \mathcal{C}.$](img218.gif) |
(21) |
Como cada cilindro
![]() es abierto, entonces
es abierto, entonces
![]() establece una cubierta finita para
establece una cubierta finita para
![]() .
.
Es aquí donde se puede apreciar la importancia que tiene la elección de un centro para definir una distancia en el espacio de configuraciones
![]() , pues dado este centro se puede definir el conjunto de cilindros y con esto generar una cubierta finita de
, pues dado este centro se puede definir el conjunto de cilindros y con esto generar una cubierta finita de
![]() concluyendo que dicho espacio es compacto. El que un espacio topológico sea compacto es muy útil ya que podemos tratar el espacio con un número finito de subconjuntos del mismo lo que facilita su estudio, veamos ahora como podemos elegir un representante de cada subconjunto.
concluyendo que dicho espacio es compacto. El que un espacio topológico sea compacto es muy útil ya que podemos tratar el espacio con un número finito de subconjuntos del mismo lo que facilita su estudio, veamos ahora como podemos elegir un representante de cada subconjunto.
En base al trabajo de Lind y Marcus en [LM95], para el espacio de configuraciones
![]() , tomemos un cilindro
, tomemos un cilindro
![]() como se establece en la ecuación 19, cons-truyamos una subsecuencia convergente de
como se establece en la ecuación 19, cons-truyamos una subsecuencia convergente de
![]() . Para
. Para ![]() , encontremos una secuencia de subconjuntos
, encontremos una secuencia de subconjuntos ![]() de enteros positivos tal que:
de enteros positivos tal que:
| (22) |
Definamos la configuración
![]() donde
donde
![]() para toda
para toda ![]() e inductivamente definamos
e inductivamente definamos ![]() como el elemento más pequeño de
como el elemento más pequeño de ![]() el cual excede a
el cual excede a ![]() . Entonces
. Entonces
![]() converge a
converge a
![]() conforme
conforme
![]() .
.
Utilizando la idea de convergencia, podemos decir que el espacio de configuraciones
![]() es compacto si cada secuencia de configuraciones en
es compacto si cada secuencia de configuraciones en
![]() converge a un configuración dada [LM95], pues esta convergencia asegura la existencia de los conjuntos de cilindros.
converge a un configuración dada [LM95], pues esta convergencia asegura la existencia de los conjuntos de cilindros.