La teoría del campo promedio ha sido empleada en [16], [22], [24], [30], [44] y [50], para tratar de explicar el comportamiento de los estados de las reglas de evolución, la mayoría de estos estudios describen el comportamiento de las células a través de su densidad en el espacio de evoluciones en el tiempo. El análisis propone un enfoque sencillo y práctico de como obtener dichas densidades e interpretar fácilmente los resultados, tal como lo plantean McIntosh en [44] y Chaté-Manneville en [16], graficando su curva de probabilidad en el tiempo inicial y calculando sus curvas de probabilidad a través del tiempo, sustituyendo iterativamente el polinomio de la Equación 2.5.1.
Se construye el polinomio de la teoría del campo promedio paso a paso para ver con claridad la relación que existe entre las Ecuaciones 2.5.1 y 2.5.7, y las variables definidas por ![]() ,
, ![]() ,
, ![]() y
y ![]() . La regla Life es la regla semiltotalística
. La regla Life es la regla semiltotalística
![]() entonces
entonces ![]() ,
, ![]() ,
, ![]() y
y ![]() , el número de configuraciones que se pueden generar en la vecindad de Moore cuando
, el número de configuraciones que se pueden generar en la vecindad de Moore cuando ![]() es igual a 28, como se ilustra en la Figura 3.9.
es igual a 28, como se ilustra en la Figura 3.9.
La transformación local cuando ![]() determina 28 vecindades que se transforman a 1 en la siguiente generación, donde la célula central en este caso es igual a 1, la Figura 3.9 ilustra todas las combinaciones que se pueden generar en la vecindad de Moore, cuando la célula central está viva y se tienen dos vecinos vivos para que en la siguiente generación la célula central siga viva. Empleando notación de las Ecuaciones 2.5.1 y 2.5.7 se representa el polinomio del campo promedio de la siguiente manera:
determina 28 vecindades que se transforman a 1 en la siguiente generación, donde la célula central en este caso es igual a 1, la Figura 3.9 ilustra todas las combinaciones que se pueden generar en la vecindad de Moore, cuando la célula central está viva y se tienen dos vecinos vivos para que en la siguiente generación la célula central siga viva. Empleando notación de las Ecuaciones 2.5.1 y 2.5.7 se representa el polinomio del campo promedio de la siguiente manera:
donde ![]() representa el número de células que tiene una vecindad,
representa el número de células que tiene una vecindad, ![]() son las combinaciones sin tomar en cuenta la célula central,
son las combinaciones sin tomar en cuenta la célula central, ![]() indica el número de veces que aparece el estado 1 en la vecindad de Moore,
indica el número de veces que aparece el estado 1 en la vecindad de Moore, ![]() indica el número de veces que aparece el estado 0 en la vecindad de Moore,
indica el número de veces que aparece el estado 0 en la vecindad de Moore, ![]() es la probabilidad de tener 1's en la siguiente generación,
es la probabilidad de tener 1's en la siguiente generación, ![]() es la probabilidad de tener 0's en la siguiente generación, la combinatoria
es la probabilidad de tener 0's en la siguiente generación, la combinatoria
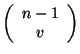 dará las constantes para cada uno de los términos del polinomio. La primera sumatoria calculará todas las combinaciones que se derivan del intervalo que definen
dará las constantes para cada uno de los términos del polinomio. La primera sumatoria calculará todas las combinaciones que se derivan del intervalo que definen ![]() y
y ![]() en el caso de la sobrevivencia. La segunda sumatoria calculará todas las combinaciones que se derivan del intervalo que definen
en el caso de la sobrevivencia. La segunda sumatoria calculará todas las combinaciones que se derivan del intervalo que definen ![]() y
y ![]() en el caso de los nacimientos. En el caso de la sobrevivencia al exponente
en el caso de los nacimientos. En el caso de la sobrevivencia al exponente ![]() se le suma un elemento, porque al momento de definir la cantidad de 1's en la vecindad la célula central está viva. En el caso de los nacimientos
se le suma un elemento, porque al momento de definir la cantidad de 1's en la vecindad la célula central está viva. En el caso de los nacimientos ![]() representa el número de veces que aparece el estado 1 en la vecindad y no se le suma ningún elemento porque la célula central está muerta.
representa el número de veces que aparece el estado 1 en la vecindad y no se le suma ningún elemento porque la célula central está muerta.
La probabilidad de que se obtengan 1's es igual a ![]() , para garantizar su complemento
, para garantizar su complemento ![]() es la probabilidad de que se obtengan 0's, por lo tanto
es la probabilidad de que se obtengan 0's, por lo tanto ![]() y
y ![]() . Simplificando la Ecuación 3.4.1 empleando la variable
. Simplificando la Ecuación 3.4.1 empleando la variable ![]() se tiene finalmente:
se tiene finalmente:
El exponente ![]() para la variable
para la variable ![]() se calcula sumando el número de células ocupadas por el estado 1 dentro de la vecindad de Moore, el exponente
se calcula sumando el número de células ocupadas por el estado 1 dentro de la vecindad de Moore, el exponente ![]() para la variable
para la variable ![]() se calcula sumando el número de células ocupadas por el estado 0 dentro de la vecindad de Moore, entonces se tiene que
se calcula sumando el número de células ocupadas por el estado 0 dentro de la vecindad de Moore, entonces se tiene que ![]() y
y ![]() , cuando
, cuando ![]() . Nótese que las combinaciones se realizan en la vecindad isotrópica
. Nótese que las combinaciones se realizan en la vecindad isotrópica
![]() (en los vecinos), donde la célula central
(en los vecinos), donde la célula central
![]() es ocupada por el estado 1, en realidad al momento de calcular las configuraciones no importa si
es ocupada por el estado 1, en realidad al momento de calcular las configuraciones no importa si
![]() es ocupada por el estado 1 o el estado 0, sin embargo
es ocupada por el estado 1 o el estado 0, sin embargo
![]() es importante al momento de definir los exponentes del polinomio.
es importante al momento de definir los exponentes del polinomio.
Ahora se realiza el cálculo cuando ![]() como se ilustra en la Figura 3.10.
como se ilustra en la Figura 3.10.
Cuando ![]() se generan 56 vecindades que se transforman al estado 1 en la siguiente generación dentro de la vecindad de Moore, éstas son combinaciones sin repetición. Por lo tanto se calcula el número de combinaciones empleando el coeficiente binomial:
se generan 56 vecindades que se transforman al estado 1 en la siguiente generación dentro de la vecindad de Moore, éstas son combinaciones sin repetición. Por lo tanto se calcula el número de combinaciones empleando el coeficiente binomial:
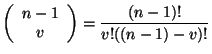 |
(3.4.3) |
donde
![]() y
y ![]() tomará valores de
tomará valores de
![]() . Por ejemplo para el caso de la Figura 3.9 se tiene que
. Por ejemplo para el caso de la Figura 3.9 se tiene que
![]() y
y
![]() , entonces se tiene que:
, entonces se tiene que:
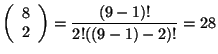 |
donde este número representa las combinaciones sin repetición que se generan cuando ![]() en la vecindad isotrópica
en la vecindad isotrópica
![]() o los vecinos de la vecindad de Moore. En el caso de la Figura 3.10 se tiene que
o los vecinos de la vecindad de Moore. En el caso de la Figura 3.10 se tiene que ![]() , entonces se tiene que:
, entonces se tiene que:
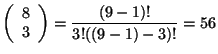 |
donde este número representa las combinaciones sin repetición que se generan cuando ![]() en la vecindad isotrópica
en la vecindad isotrópica
![]() o los vecinos de la vecindad de Moore. Nótese que para el caso cuando
o los vecinos de la vecindad de Moore. Nótese que para el caso cuando ![]() y
y ![]() , se tienen 56 combinaciones igual que cuando
, se tienen 56 combinaciones igual que cuando ![]() , ésto se debe porque las combinaciones se realizan en las células de
, ésto se debe porque las combinaciones se realizan en las células de
![]() , es decir, los vecinos de la vecindad sin tomar en cuenta la célula central
, es decir, los vecinos de la vecindad sin tomar en cuenta la célula central
![]() , por lo que las combinaciones de
, por lo que las combinaciones de ![]() son iguales a las combinaciones de
son iguales a las combinaciones de ![]() y
y ![]() , estos valores van a determinar las constantes del polinomio.
, estos valores van a determinar las constantes del polinomio.
El grado del polinomio se determina por el número de células vivas ![]() y por el número de células muertas
y por el número de células muertas ![]() , que existen en los vecinos
, que existen en los vecinos
![]() de las Figuras 3.9 y 3.10, cuando
de las Figuras 3.9 y 3.10, cuando ![]() se tiene que
se tiene que ![]() y
y ![]() , cuando
, cuando ![]() se tiene que
se tiene que ![]() y
y ![]() , cuando
, cuando ![]() se tiene que
se tiene que ![]() y
y ![]() y cuando
y cuando ![]() se tiene que
se tiene que ![]() y
y ![]() , finalmente el polinomio para la regla de Life es:
, finalmente el polinomio para la regla de Life es:
simplificando se tiene el polinomio de la teoría del campo promedio para Life:
la probabilidad que se genera cuando ![]() es la misma probabilidad cuando
es la misma probabilidad cuando ![]() , porque el número de 1's en la vecindad de Moore es igual en los dos casos, por eso se tienen tres términos en el polinomio en lugar de cuatro como pudiera pensarse.
, porque el número de 1's en la vecindad de Moore es igual en los dos casos, por eso se tienen tres términos en el polinomio en lugar de cuatro como pudiera pensarse.
La curva de probabilidad se obtiene poniendo el polinomio de la Ecuación 3.4.5 en términos de ![]() :
:
donde ![]() tomará valores de 0 a 1. La curva de probabilidad del campo promedio muestra directamente la información de como se comporta la densidad de los estados en el espacio de evoluciones. La densidad es interpretada a través de la existencia de puntos fijos en la curva de probabilidad que genera el polinomio. A continuación se da la definición de punto fijo.
tomará valores de 0 a 1. La curva de probabilidad del campo promedio muestra directamente la información de como se comporta la densidad de los estados en el espacio de evoluciones. La densidad es interpretada a través de la existencia de puntos fijos en la curva de probabilidad que genera el polinomio. A continuación se da la definición de punto fijo.
Los puntos fijos pueden ser estables o inestables. Sea ![]() una función diferenciable, si el valor absoluto de la primera derivada
una función diferenciable, si el valor absoluto de la primera derivada ![]() , entonces
, entonces ![]() es un punto fijo estable. Si el valor absoluto de la primera derivada
es un punto fijo estable. Si el valor absoluto de la primera derivada ![]() entonces
entonces ![]() es un punto fijo inestable. Si el valor de la primera derivada
es un punto fijo inestable. Si el valor de la primera derivada ![]() , entonces
, entonces ![]() es llamado un punto crítico, es decir, su tangente es horizontal al eje
es llamado un punto crítico, es decir, su tangente es horizontal al eje ![]() en el plano cartesiano.
en el plano cartesiano.
La gráfica de la Figura 3.11 muestra la curva de probabilidad que produce el polinomio de la regla de evolución Life, el eje horizontal ![]() indicará la probabilidad de obtener 0's, el eje vertical
indicará la probabilidad de obtener 0's, el eje vertical ![]() indica la probabilidad de obtener 1's,
indica la probabilidad de obtener 1's, ![]() y
y ![]() podrán ser evaluados en el intervalo cerrado
podrán ser evaluados en el intervalo cerrado ![]() , por esta razón la diagonal mostrará los punto fijos de la curva al momento de intersectar algún punto de la curva con la diagonal, porque eso significa que
, por esta razón la diagonal mostrará los punto fijos de la curva al momento de intersectar algún punto de la curva con la diagonal, porque eso significa que ![]() en ese punto.
en ese punto.
El punto fijo estable que se encuentra en 0 sobre el eje ![]() de la Figura 3.11 indica que en el espacio de evoluciones no hay células vivas, entonces la probabilidad de que se obtengan células vivas en la siguiente generación es 0, ésto es por la condición de que
de la Figura 3.11 indica que en el espacio de evoluciones no hay células vivas, entonces la probabilidad de que se obtengan células vivas en la siguiente generación es 0, ésto es por la condición de que
![]() ; por otra parte si el espacio de evoluciones se encuentra lleno de células vivas, entonces la probabilidad de que se obtengan células vivas en la siguiente generación es 0, esto se debe por la condición de que
; por otra parte si el espacio de evoluciones se encuentra lleno de células vivas, entonces la probabilidad de que se obtengan células vivas en la siguiente generación es 0, esto se debe por la condición de que
![]() y los valores de la curva son igual a 0 conforme nos acerquemos mas a 1 en el eje
y los valores de la curva son igual a 0 conforme nos acerquemos mas a 1 en el eje ![]() .
.
Nótese la existencia de otros dos puntos fijos, un punto fijo inestable aproximadamente en 0.2 que indica la existencia de comportamientos inpredecibles dentro de ciertas regiones locales, es decir, la densidad que tiene el autómata en ese momento puede mantenerse igual, crecer rápidamente o desaparecer por completo en unos cuantos pasos. El otro punto fijo es un punto crítico y se encuentra aproximadamente en 0.37 que indica la densidad promedio de células vivas que se pueden conservar en el espacio de evoluciones a través del tiempo. Para obtener el comportamiento en la siguiente generación se sustituye el polinomio ![]() de la Ecuación 3.4.6, en él mismo para obtener la curva de probabilidad en
de la Ecuación 3.4.6, en él mismo para obtener la curva de probabilidad en ![]() de la siguente manera:
de la siguente manera:
este polinomio mostrará el comportamiento de la curva en la siguiente generación. Nótese que conforme se desee calcular mas generaciones el polinomio crece exponencialmente, los polinomios para la tercera y cuarta generación ocuparían tres páginas completas. En la Figura 3.12 se grafican las curvas de probabilidad para la segunda, tercera y cuarta generación de la regla de evolución Life.
El comportamiento de las células en cada generación delimita cada vez mas su densidad en el espacio de evoluciones, en promedio éste es el comportamiento que debe seguir cualquier configuración inicial aleatoria, se puede apreciar en la Figura 3.12 que el intervalo de la curva sobre el eje ![]() se hace cada vez mas estrecho, ésto indica que la población de células vivas es cada vez menor, en efecto así ocurre en Life.
se hace cada vez mas estrecho, ésto indica que la población de células vivas es cada vez menor, en efecto así ocurre en Life.
En la fase de experimentación las curvas de probabilidad se calcularon sustituyendo el polinomio ![]() en
en ![]() , el polinomio
, el polinomio ![]() en
en ![]() y así sucesivamente. Para tratar de acelerar el proceso en las curvas de probabilidad se sustituyo el polinomio
y así sucesivamente. Para tratar de acelerar el proceso en las curvas de probabilidad se sustituyo el polinomio ![]() en
en ![]() , el polinomio
, el polinomio ![]() en
en ![]() y así sucesivamente, pero los resultados al momento de generar la gráfica fueron idénticos, además de que para el segundo caso existe el problema de que el polinomio a calcular es mucho mas grande que para el primer caso.
y así sucesivamente, pero los resultados al momento de generar la gráfica fueron idénticos, además de que para el segundo caso existe el problema de que el polinomio a calcular es mucho mas grande que para el primer caso.
La densidad promedio de 0.37 calculada para la regla de evolución Life coincide con otros resultados obtenidos en [50] y [24]. Todos los demás casos se estudian de la misma manera, para posteriormente establecer una caracterización a través de sus curvas de probabilidad.