 es continua en un punto
es continua en un punto 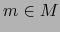 .
.
- Para todo mapa admisible
 de
de  en el punto
en el punto 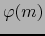 existe
un mapa admisible
existe
un mapa admisible  de
de  en el punto
en el punto  tal que:
tal que:
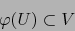
Demostración
Basta probar la afirmación siguiente:
SiSea, pues,es una variedad
y
, las vecindades abiertas
de
en
, tales que existe un mapa admisible
de
, constituyen un sistema fundamental de vecindades de
.

Informalmente se dice que la aplicación:
Demostración
Con las notaciones de la definición 5.2.1, la aplicación
![]() diferenciable C.D. en el punto
diferenciable C.D. en el punto ![]() del abierto
del abierto ![]() de un espacio vectorial real es continua en él en virtud del teorema 4.3.2.
La aplicación
de un espacio vectorial real es continua en él en virtud del teorema 4.3.2.
La aplicación ![]() restringida a
restringida a ![]() puede escribirse:
puede escribirse:
La definición 5.2.1 es manejable merced al:
Demostración
Sean
![]() mapas admisibles como en la definición 5.2.1.
Por
hipótesis la aplicación
mapas admisibles como en la definición 5.2.1.
Por
hipótesis la aplicación
![]() es diferenciable C.D. en el punto
es diferenciable C.D. en el punto ![]() de
de ![]() . Sean ahora
. Sean ahora
![]() ,
,
![]() mapas admisibles de sendas variedades
mapas admisibles de sendas variedades ![]() ,
, ![]() en sendos puntos
en sendos puntos ![]() ,
, ![]() tales que
tales que
![]() Restringiendo
Restringiendo
![]() a
a
![]() y
y
![]() a
a
![]() podemos escribir:
podemos escribir:
![]() como ya se ha dicho, es diferenciable C.D. en
como ya se ha dicho, es diferenciable C.D. en ![]() y manda
y manda ![]() sobre
sobre ![]() . A su vez el
cambio de mapa
. A su vez el
cambio de mapa
![]() es un isomorfismo
es un isomorfismo
![]() de
de
![]() sobre
sobre
![]() , en particular es diferenciable C.D.
en el punto
, en particular es diferenciable C.D.
en el punto
![]() y lo manda sobre
y lo manda sobre ![]() .
.
En virtud del teorema 4.4.4, la relación (2) entraña que
![]() es diferenciable C.D. en el punto
es diferenciable C.D. en el punto ![]() .
.
![]()
Observación (Permanencia de la definición)
Notamos que si ![]() es un abierto de
es un abierto de
![]() ,
, ![]() provisto del atlas
admisible reducido al solo mapa
provisto del atlas
admisible reducido al solo mapa
![]() , donde
, donde
![]() es
la aplicación idéntica de
es
la aplicación idéntica de ![]() , constituye una variedad
, constituye una variedad ![]() de dimensión
de dimensión ![]() .
Es una subvariedad abierta de
.
Es una subvariedad abierta de
![]() , provisto éste del atlas admisible reducido
al mapa
, provisto éste del atlas admisible reducido
al mapa
![]() .
.
Esta estructura de variedad ![]() sobre
sobre ![]() se llama la ESTRUCTURA NATURAL de variedad
se llama la ESTRUCTURA NATURAL de variedad ![]() sobre
sobre ![]() . A menos de una indicación contraria,
será la única considerada sobre el abierto
. A menos de una indicación contraria,
será la única considerada sobre el abierto ![]() de
de
![]() .
.
Sean ahora ![]() un abierto de
un abierto de
![]() ,
, ![]() un abierto de
un abierto de
![]() y
y ![]() una aplicación
una aplicación ![]() .
. ![]() leída en los mapas
leída en los mapas
![]() y
y
![]() coincide con la propia
coincide con la propia ![]() . Así pues,:
. Así pues,:
![]() es diferenciable en un punto
es diferenciable en un punto ![]() según la definición 5.2.1
si y sólo si
según la definición 5.2.1
si y sólo si ![]() es diferenciable C.D. en m.
es diferenciable C.D. en m.
Para el caso más general de aplicaciones entre abiertos de espacios afines vea el siguiente §3.
Demostración
Pero
![]() .
.
Así pues,
![]() leída en los mapas
leída en los mapas ![]() y
y ![]() es diferenciable C.D.
en el punto
es diferenciable C.D.
en el punto ![]() . Esto significa que
. Esto significa que
![]() es diferenciable en el punto
es diferenciable en el punto ![]() .
.
![]()
Nota
Para aplicaciones de una variedad ![]() en otra hemos definido
el concepto de diferenciabilidad en un punto, pero todavía no aquél
de diferencial. Para formular una definición de ésta, análoga a la que tenemos
en espacios afines, necesitamos la noción previa de vectores tangentes en un punto
de una variedad
en otra hemos definido
el concepto de diferenciabilidad en un punto, pero todavía no aquél
de diferencial. Para formular una definición de ésta, análoga a la que tenemos
en espacios afines, necesitamos la noción previa de vectores tangentes en un punto
de una variedad ![]() . Será introducida en el capítulo 6.
. Será introducida en el capítulo 6.