




Siguiente: Diferenciabilidad de funciones reales
Arriba: Aplicaciones diferenciables
Anterior: Aplicaciones diferenciables
Dentro del marco de nuestro curso, un espacio afín normado de dimensión infinita
no es una variedad diferenciable.
Sin embargo, imitando la definición 5.2.1, podemos formular la:
Definición 2.2
Sean  una variedad
una variedad  y
y  una aplicación de
una aplicación de  en un espacio afín
normado
en un espacio afín
normado  . Se dice que la aplicación
. Se dice que la aplicación  es DIFERENCIABLE EN UN PUNTO
es DIFERENCIABLE EN UN PUNTO  de
de  , si existe un mapa admisible
, si existe un mapa admisible 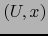 de
de  en
en  tal que la aplicación
tal que la aplicación
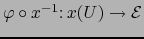 es diferenciable C.D. en el punto
es diferenciable C.D. en el punto
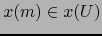 .
.
Esta definición es manejable gracias al:
Teorema 2.5
Si, con las notaciones de la definición 5.2.2 la aplicación  es diferenciable en el punto
es diferenciable en el punto 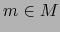 , para todo mapa admisible
, para todo mapa admisible
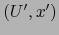 de
la variedad
de
la variedad  en el punto
en el punto  la aplicación
la aplicación
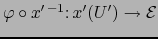 es diferenciable C.D. en el punto
es diferenciable C.D. en el punto 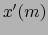 .
.
Demostración
La demostración es parecida a la del teorema 5.2.3 pero más simple. Restringiendo
la aplicación
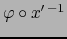 a la vecindad abierta
a la vecindad abierta
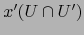 del
punto
del
punto
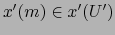 podemos escribir:
podemos escribir:
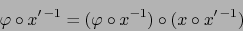 |
(3) |
El cambio de mapa
 es
de clase
es
de clase  a fortiori diferenciable C.D. en el punto
a fortiori diferenciable C.D. en el punto 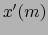 . Por hipótesis
. Por hipótesis
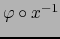 es diferenciable C.D. en
es diferenciable C.D. en 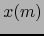 . De (3) y el
teorema 4.4.4, se sigue que
. De (3) y el
teorema 4.4.4, se sigue que
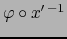 es también diferenciable C.D. en el punto
es también diferenciable C.D. en el punto 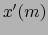 .
.






Siguiente: Diferenciabilidad de funciones reales
Arriba: Aplicaciones diferenciables
Anterior: Aplicaciones diferenciables
Guillermo M. Luna
2009-06-14
![]() a la vecindad abierta
a la vecindad abierta
![]() del
punto
del
punto
![]() podemos escribir:
podemos escribir: