




Siguiente: Aplicaciones de clase
Arriba: Aplicaciones diferenciables
Anterior: Diferenciabilidad de una aplicación
Teorema 2.6
Sean  una variedad
una variedad  y
y 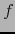 ,
, 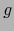 funciones
funciones
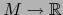 .
.
- Si
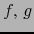 son diferenciables en un punto
son diferenciables en un punto 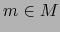 , entonces para todos
, entonces para todos
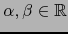 , la función
, la función
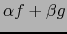 es
diferenciable en el punto
es
diferenciable en el punto  .
.
- Si
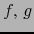 son diferenciables en
son diferenciables en  , la función
, la función 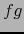 es
diferenciable en
es
diferenciable en  .
.
- Si
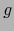 es continua en
es continua en  mientras
mientras 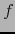 es diferenciable en
es diferenciable en  y cumple
y cumple 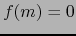 , la función
, la función 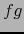 es diferenciable en
es diferenciable en  .
.
Demostración
Sea 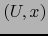 un mapa admisible de la variedad
un mapa admisible de la variedad  en el punto
en el punto  . En
. En
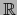 usamos el único mapa admisible
usamos el único mapa admisible
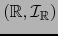 .
.
Si 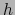 es una función
es una función
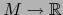 ,
, 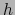 leída en los mapas
considerados es la función
leída en los mapas
considerados es la función
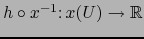 ,
, 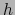 será, pues, diferenciable en el punto
será, pues, diferenciable en el punto 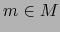 si y sólo si
si y sólo si
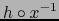 es diferenciable C.D. en el punto
es diferenciable C.D. en el punto 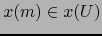 .
.
- Supongamos
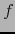 y
y 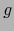 diferenciables en el punto
diferenciables en el punto 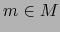 ,
vale decir
,
vale decir
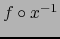 y
y
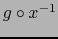 diferenciables C.D. en el
punto
diferenciables C.D. en el
punto 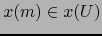 .
.
Por el teorema 4.3.5,
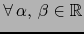 es
diferenciable C.D. en el punto
es
diferenciable C.D. en el punto 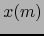 , la función:
, la función:
es decir, la función
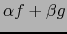 es diferenciable en el punto
es diferenciable en el punto
 .
.
- Adoptemos la hipótesis del inciso a). Por el teorema 4.3.5, es
diferenciable C.D. en el punto
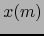 , la función:
, la función:
Por lo tanto, 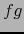 es diferenciable en el punto
es diferenciable en el punto  .
.
- Supongamos finalmente
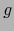 continua en
continua en  ,
, 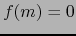 y
y 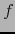 diferenciable en
diferenciable en  .
.
Estas hipótesis equivalen a que
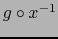 es continua en el
punto
es continua en el
punto 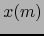 ,
,
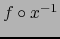 se anula en dicho punto
se anula en dicho punto 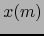 y es
diferenciable C.D. en él.
y es
diferenciable C.D. en él.
Por el teorema 4.3.5, la función:
es diferenciable C.D. en el punto 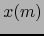 . Equivalentemente,
. Equivalentemente, 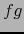 es
diferenciable en el punto
es
diferenciable en el punto  .
.






Siguiente: Aplicaciones de clase
Arriba: Aplicaciones diferenciables
Anterior: Diferenciabilidad de una aplicación
Guillermo M. Luna
2009-06-14
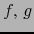 son diferenciables en un punto
son diferenciables en un punto 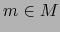 , entonces para todos
, entonces para todos
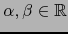 , la función
, la función
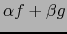 es
diferenciable en el punto
es
diferenciable en el punto  .
.
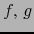 son diferenciables en
son diferenciables en  , la función
, la función 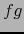 es
diferenciable en
es
diferenciable en  .
.
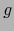 es continua en
es continua en  mientras
mientras 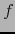 es diferenciable en
es diferenciable en  y cumple
y cumple 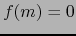 , la función
, la función 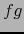 es diferenciable en
es diferenciable en  .
.