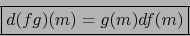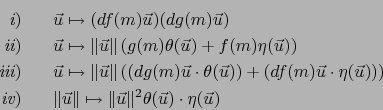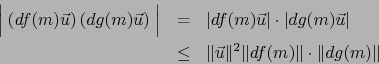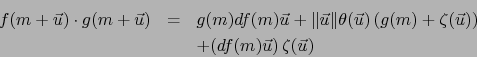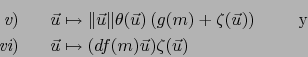Supongamos de nuevo que  y
y  son diferenciables en
son diferenciables en  y usemos otra vez las relaciones (15) y (16). Al multiplicar éstas miembro por
miembro, conseguimos:
y usemos otra vez las relaciones (15) y (16). Al multiplicar éstas miembro por
miembro, conseguimos:
Aquí
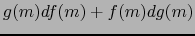 es, de nuevo, una forma lineal continua sobre
es, de nuevo, una forma lineal continua sobre  , elemento de
, elemento de 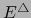 . Resta probar que las funciones:
. Resta probar que las funciones:
son, como se dice ``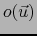 '' es decir que, divididas por
'' es decir que, divididas por 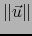 tienden a cero cuando
tienden a cero cuando 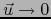 .
.
Por la fórmula (6) en las definiciones 4.2.3, la función i) se mayora mediante:
donde en los dos últimos factores las normas son aquellas sobre 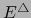 . Esta mayoración
implica que la función i) es
. Esta mayoración
implica que la función i) es 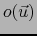 .
.
La función ii) es 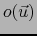 , pues el factor de
, pues el factor de 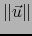 tiende a cero para
tiende a cero para 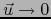 debido a (17). También el
factor de
debido a (17). También el
factor de 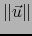 en iii) tiende a cero por (17) y por ser también
en iii) tiende a cero por (17) y por ser también
Lo último resulta de que 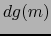 y
y  son formas lineales continuas.
son formas lineales continuas.
Es obvio, por fin, que la función iv) es 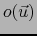 .
.
La afirmación b) queda, pues,
demostrada.
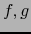 son diferenciables en el punto
son diferenciables en el punto  , es también diferenciable en el punto
, es también diferenciable en el punto  la
función
la
función
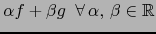 y vale:
y vale:
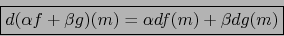
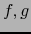 son diferenciables en el punto
son diferenciables en el punto  , también es diferenciable en
, también es diferenciable en  la función
la función 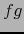 y vale:
y vale:
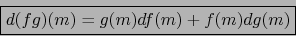
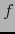 es diferenciable en
es diferenciable en  , vale
, vale 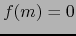 y además
y además 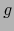 es continua en
es continua en  , la función
, la función 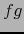 es diferenciable
en
es diferenciable
en  y tenemos:
y tenemos: