




Siguiente: Caracterización de mapas admisibles
Arriba: Aplicaciones de clase
Anterior: Aplicaciones de clase
Teorema 3.3
Sean  una variedad
una variedad  y
y  una aplicación
una aplicación
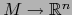
 es diferenciable en un punto
es diferenciable en un punto 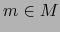 si y sólo
si para algún mapa admisible
si y sólo
si para algún mapa admisible  de
de  en
en  (luego para todo tal mapa
admisible) la aplicación
(luego para todo tal mapa
admisible) la aplicación
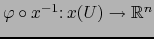 es diferenciable
(C.D.) en el punto
es diferenciable
(C.D.) en el punto  .
.
- Sea
![$j \in [\![ 1, k ]\!]$](img4245.png) . La aplicación
. La aplicación  es de clase
es de clase  en
en  si y sólo
si para todo punto
si y sólo
si para todo punto 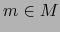 existe un mapa admisible
existe un mapa admisible  de
de  en
en  tal que la
aplicación
tal que la
aplicación
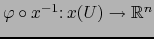 es de clase
es de clase  (C.D.)
en
(C.D.)
en 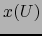 . (Luego lo mismo ocurre para todo mapa admisible
. (Luego lo mismo ocurre para todo mapa admisible  de M).
de M).
Esto resulta sin más de las definiciones 5.2.1 y 5.2.2 y de
los teorema 5.2.3 y 5.3.1 al usar el mapa
 admisible para la estructura
natural de variedad
admisible para la estructura
natural de variedad  sobre
sobre
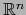 .
.
Ejemplo 5.1.
Si M es una variedad  y
y 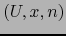 es cualquier mapa admisible de M la aplicación
es cualquier mapa admisible de M la aplicación
 es de clase
es de clase  .
.
Basta aplicar el teorema 5.3.2 parte b) con 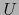 en papel de
en papel de  y
y 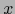 en el papel
de
en el papel
de  . Si
. Si
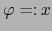 vale
vale
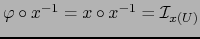 ,
que es de clase
,
que es de clase  en
en 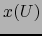 por el teorema 5.3.2. Luego
por el teorema 5.3.2. Luego 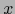 es de clase
es de clase
 en
en 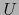 .
. 
Teorema 3.4
Sean  una variedad
una variedad  ,
, 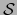 un abierto de
un abierto de
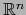 y
y  una aplicación
una aplicación
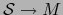 .
.
 es diferenciable en un punto
es diferenciable en un punto 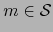 si y sólo si
si y sólo si
 es continua en
es continua en  y existe un mapa admisible
y existe un mapa admisible  de
de  en el punto
en el punto
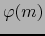 tal que la aplicación
tal que la aplicación
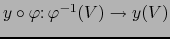 es diferenciable C.D. en el punto
es diferenciable C.D. en el punto  . (Entonces lo mismo ocurre para todo mapa
admisible
. (Entonces lo mismo ocurre para todo mapa
admisible  de
de  en el punto
en el punto 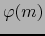 .)
.)
- Sea
![$j \in [\![ 1, k ]\!]$](img4245.png) .
.  es de clase
es de clase  en
en 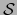 si y sólo si
es continua y
si y sólo si
es continua y
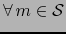 existe un mapa admisible
existe un mapa admisible  de
de
 en
en 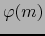 tal que la aplicación
tal que la aplicación
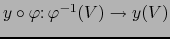 es de clase
es de clase  (C.D.) en
(C.D.) en
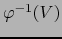 . (Entonces lo mismo ocurre para cualquier
mapa admisible
. (Entonces lo mismo ocurre para cualquier
mapa admisible  de
de  .)
.)
Demostración
- Supongamos
 diferenciable en el punto
diferenciable en el punto 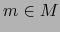 . Por el teorema
5.2.2
. Por el teorema
5.2.2  es continua en
es continua en  . Sea
. Sea  un mapa admisible de
un mapa admisible de  en
en 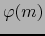 .
.  es una vecindad de
es una vecindad de 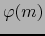 , luego, por continuidad
, luego, por continuidad
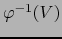 es una vecindad de
es una vecindad de  en
en 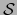 , o sea,
, o sea,  es un punto interior de
es un punto interior de
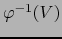 . Sea
. Sea
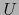 una vecindad abierta de
una vecindad abierta de  contenida en
contenida en
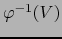 . Vale
. Vale
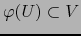 . Por
el teorema 5.2.3, aplicado a los mapas admisibles
. Por
el teorema 5.2.3, aplicado a los mapas admisibles
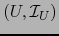 de
de 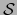 en
en  y
y
 de
de  en
en 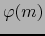 , la aplicación
, la aplicación
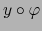 restringida a
restringida a
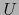 es diferenciable C.D. en
es diferenciable C.D. en  . Por la propiedad local
de la diferencial lo mismo ocurre para la aplicación ampliada
. Por la propiedad local
de la diferencial lo mismo ocurre para la aplicación ampliada
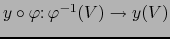
Recíprocamente supongamos  continua en
continua en  y que existe un mapa admisible
y que existe un mapa admisible
 de
de  en
en 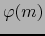 tal que
tal que
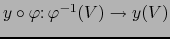 es
diferenciable C.D. en
es
diferenciable C.D. en  . Esta afirmación tiene sentido, pues, por continuidad de
. Esta afirmación tiene sentido, pues, por continuidad de  en
en  el conjunto
el conjunto
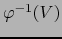 es un a vecindad de
es un a vecindad de  , o sea
, o sea  es un punto interior de
es un punto interior de
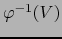 .
.
Sea 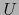 una vecindad abierta de
una vecindad abierta de  contenida en
contenida en
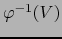 . Por el carácter local de
la diferencial también
. Por el carácter local de
la diferencial también
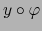 restringida a
restringida a 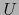 es diferenciable C.D. en
es diferenciable C.D. en  . Por
el teorema 5.2.3 aplicado a los mapas admisibles
. Por
el teorema 5.2.3 aplicado a los mapas admisibles
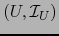 en
en 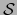 en
en
 y
y  de
de  en
en 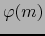 ,
,  es diferenciable en
es diferenciable en  .
.
- Sea
![$j \in [\![ 1, k ]\!]$](img4245.png) . Supongamos que
. Supongamos que  es de clase
es de clase  en
en
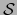 . Esto implica que
. Esto implica que  es continua. Sean
es continua. Sean 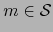 y
y  un mapa admisible de
un mapa admisible de  en
en
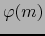 . Por continuidad
. Por continuidad
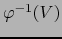 es un abierto de
es un abierto de 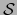 que contiene
que contiene  .
.
Aplicando el teorema 5.2.5 a los mapas
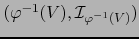 admisible para
admisible para
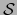 y
y  admisible para
admisible para  , vemos que la aplicación
, vemos que la aplicación
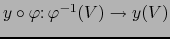 es
de clase
es
de clase  (C.D.) en
(C.D.) en
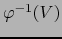 .
.
Recíprocamente supongamos que  es continua y que
es continua y que
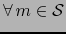 existe un mapa admisible
existe un mapa admisible  de
de  en el punto
en el punto 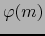 tal que la aplicación
tal que la aplicación
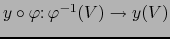 es de clase
es de clase  (C.D.) en
(C.D.) en
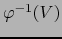 .
.
Esta afirmación tiene sentido, pues, por continuidad de  el conjunto
el conjunto
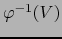 es un abierto en
es un abierto en  . Aplicando la definición 5.2.2 a los mapas
. Aplicando la definición 5.2.2 a los mapas
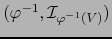 admisible para
admisible para 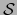 y
y  admisible
para
admisible
para  , vemos que
, vemos que  es de clase
es de clase  en
en 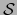 .
.

Ejemplo 5.2
Si M es una variedad  y
y 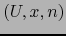 es cualquier mapa admisible de M la aplicación:
es cualquier mapa admisible de M la aplicación:
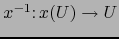 es de clase
es de clase 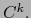
Demostración
Aplicamos el teorema 5.3.4 con
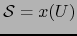 ,
,  y
y
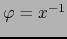 .
.  es continua. Basta usar el solo mapa admisible
es continua. Basta usar el solo mapa admisible  de
de 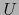 .
.
Vale
 .
. 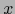 desempeña el papel de
desempeña el papel de 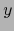 del teorema 5.3.4 y se verifica en
del teorema 5.3.4 y se verifica en 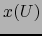 :
:
La aplicación
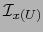 es de clase
es de clase  en
en 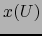 . De ahí, por
el teorema 5.3.4,
. De ahí, por
el teorema 5.3.4, 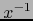 es de clase
es de clase  en
en 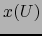 .
.






Siguiente: Caracterización de mapas admisibles
Arriba: Aplicaciones de clase
Anterior: Aplicaciones de clase
Guillermo M. Luna
2009-06-14
 es diferenciable en un punto
es diferenciable en un punto 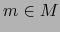 si y sólo
si para algún mapa admisible
si y sólo
si para algún mapa admisible  de
de  en
en  (luego para todo tal mapa
admisible) la aplicación
(luego para todo tal mapa
admisible) la aplicación
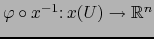 es diferenciable
(C.D.) en el punto
es diferenciable
(C.D.) en el punto  .
.
![$j \in [\![ 1, k ]\!]$](img4245.png) . La aplicación
. La aplicación  es de clase
es de clase  en
en  si y sólo
si para todo punto
si y sólo
si para todo punto 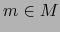 existe un mapa admisible
existe un mapa admisible  de
de  en
en  tal que la
aplicación
tal que la
aplicación
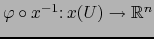 es de clase
es de clase  (C.D.)
en
(C.D.)
en 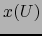 . (Luego lo mismo ocurre para todo mapa admisible
. (Luego lo mismo ocurre para todo mapa admisible  de M).
de M).