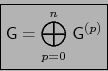Siguiente: Identificación del subespacio con
Arriba: Álgebra de Grassmann asociada
Anterior: El espacio vectorial G
![$\forall \, H \subset [\![ 1,n ]\!]$](img146.png) , designaremos por
, designaremos por 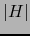 la cardinalidad (número de elementos) del conjunto
la cardinalidad (número de elementos) del conjunto 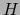 .
.
![$\forall p \in [\![ 0,n ]\!]$](img149.png) llamaremos provisionalmente
llamaremos provisionalmente
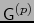 al subespacio vectorial de G engendrado
por la subfamilia
al subespacio vectorial de G engendrado
por la subfamilia
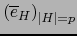 de la base
de la base
![$\left( {\overline{e}}_H \right)_{H\subset [\![ 1,n ]\!]}$](img152.png) de
G. La cardinalidad de dicha subfamilia es
de
G. La cardinalidad de dicha subfamilia es
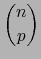 , luego:
, luego:
Un elemento 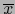 de G se dice ELEMENTO HOMOGÉNEO si existe
de G se dice ELEMENTO HOMOGÉNEO si existe
![$p \in [\![ 0,n ]\!]$](img156.png) tal que
tal que
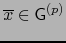 . Más específicamente, tal elemento se dice ELEMENTO HOMOGÉNEO DE GRADO
. Más específicamente, tal elemento se dice ELEMENTO HOMOGÉNEO DE GRADO 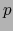 o -VECTOR. (Si
o -VECTOR. (Si 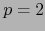 se dice
BIVECTOR, si
se dice
BIVECTOR, si 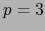 se dice TRIVECTOR, etc.).
se dice TRIVECTOR, etc.).
Claramente el espacio vectorial G es la suma directa de los subespacios
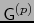 para
para
![$p \in [\![ 0,n ]\!]$](img156.png) :
:
Convendremos también en poner:
Observación
Se desprende, por ejemplo, de la tabla de multiplicación la implicación:
Brevemente (para elementos homogéneos no nulos):
Aquí ``gr'' significa ``grado''.
Guillermo M. Luna
2009-06-14
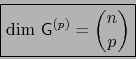
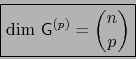
![]() para
para
![]() :
: