




Siguiente: Relación entre el álgebra
Arriba: Álgebra de Grassmann asociada
Anterior: Elementos homogéneos del álgebra
Ya que
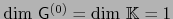 ,
, 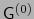 y
y  considerados como espacios vectoriales sobre
considerados como espacios vectoriales sobre  son isomorfos. Más precisamente la aplicación
son isomorfos. Más precisamente la aplicación
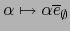 es un isomorfismo
natural (o ``canónico'') de
es un isomorfismo
natural (o ``canónico'') de  sobre el subespacio
sobre el subespacio
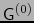 de G. (la ``naturalidad''
de dicho isomorfismo resulta de que
de G. (la ``naturalidad''
de dicho isomorfismo resulta de que
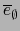 es el ele-menelemento uno del álgebra G).
es el ele-menelemento uno del álgebra G).
Mediante dicho isomorfismo convenimos una vez para siempre en identificar
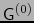 con
con  . Escribimos pues
. Escribimos pues
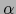 en vez de
en vez de
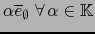 .
.
La regla
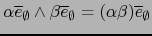 muestra que de
hecho la multiplicación exterior en
muestra que de
hecho la multiplicación exterior en
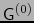 , junto con la adición hacen de
, junto con la adición hacen de
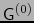 un cuerpo
isomorfo a
un cuerpo
isomorfo a  y la aplicación
y la aplicación
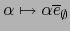 que identifica
que identifica  con
con
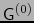 de hecho un isomorfismo de cuerpos.
de hecho un isomorfismo de cuerpos.
Más aún, la regla:
muestra que la multiplicación
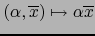 de un escalar
de un escalar 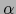 por un elemento arbitrario
por un elemento arbitrario
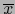 de G es un caso particular de la multiplicación exterior en G. Observamos de paso que también vale
de G es un caso particular de la multiplicación exterior en G. Observamos de paso que también vale
y que la familia reducida al solo 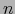 -vector
-vector
![$\overline{e}_{[\![ 1,n ]\!]}$](img177.png) constituye una base de
constituye una base de
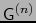 . Pero nuestro
convenio que identifica
. Pero nuestro
convenio que identifica
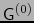 con
con  nos impide terminantemente identificar
nos impide terminantemente identificar
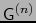 con
con  , lo
que sería una flagrante contradicción. Mencionamos dicho asunto, pues algunos vulgarizadores de la obra de Grassmann cayeron en esta contradicción.
, lo
que sería una flagrante contradicción. Mencionamos dicho asunto, pues algunos vulgarizadores de la obra de Grassmann cayeron en esta contradicción.





Siguiente: Relación entre el álgebra
Arriba: Álgebra de Grassmann asociada
Anterior: Elementos homogéneos del álgebra
Guillermo M. Luna
2009-06-14
![]() ,
, ![]() y
y ![]() considerados como espacios vectoriales sobre
considerados como espacios vectoriales sobre ![]() son isomorfos. Más precisamente la aplicación
son isomorfos. Más precisamente la aplicación
![]() es un isomorfismo
natural (o ``canónico'') de
es un isomorfismo
natural (o ``canónico'') de ![]() sobre el subespacio
sobre el subespacio
![]() de G. (la ``naturalidad''
de dicho isomorfismo resulta de que
de G. (la ``naturalidad''
de dicho isomorfismo resulta de que
![]() es el ele-menelemento uno del álgebra G).
es el ele-menelemento uno del álgebra G).
![]() con
con ![]() . Escribimos pues
. Escribimos pues
![]() en vez de
en vez de
![]() .
.
![]() muestra que de
hecho la multiplicación exterior en
muestra que de
hecho la multiplicación exterior en
![]() , junto con la adición hacen de
, junto con la adición hacen de
![]() un cuerpo
isomorfo a
un cuerpo
isomorfo a ![]() y la aplicación
y la aplicación
![]() que identifica
que identifica ![]() con
con
![]() de hecho un isomorfismo de cuerpos.
de hecho un isomorfismo de cuerpos.