Siguiente: Caso de variedades con Arriba: Diferenciación Anterior: Diferenciación

Consideraciones heurísticas

Sean $M,\, N$ variedades $C^k$ y $\varphi$ una aplicación $M \to N$ diferenciable (según la definición 5.2.2) en un punto $m \in M$.

En el caso particular de ser $M$ un abierto de un espacio afín $\cal$ de dimensión finita y $N$ un espacio afín $\cal F$ de dimensión finita, la diferencial $d \varphi (m)$ es una aplicación lineal $E \to F$ donde $E$, $F$ son espacios vectoriales asociados con sendos espacios afines $\cal E$, $\cal F$. Para transformar este enunciado en uno generalizable al caso general, podemos identificar mediante el teorema de Ellis los espacios $E$, $F$ con sendos espacios vectoriales tangente ${\cal E}_m$ y ${\cal F}_{\varphi (m)}$ y considerar $d \varphi (m)$ como aplicación lineal del espacio vectorial ${\cal E}_m$ en el espacio vectorial ${\cal F}_{\varphi (m)}$.

Deseamos caracterizar ésta de suerte que se deje generalizar inmediatamente al caso de variedades diferenciables $M$, $N$ como una aplicación lineal de $M_m$ en $N_{\varphi(m)}$.

Sea $\vec u \in E$. Por el teorema de Ellis, $\vec u$ se identifica con la funcional ${ {\partial \over\partial \vec u} (m) \in {\cal E}_m}$. ¿Con cuál elemento de ${\cal F}_{\varphi (m)}$ se ha de identificar el vector $\vec v = \colon d \varphi (m) \vec u \in F$ ?

$\forall \, g \in {\cal D}(\varphi (m))$ tenemos:

$${\partial \over \partial \vec v }(\varphi (m)) \cdot g = \lef... ...ft\langle d \varphi (m) \vec u, d g (\varphi(m)) \right\rangle$$

o sea, por la regla de la cadena:

$${\partial \over \partial \vec v} ( \varphi(m))\cdot g = \left... ...e= {\partial \over \partial \vec u} (m) \cdot (g \circ \varphi)$$

Así pues: El vector $\vec v = d \varphi (m) \vec u \in F$ se identifica por el teorema de Ellis con la funcional:

$$g \mapsto {\partial \over \partial \vec u}(m) \cdot (g \circ \varphi) \colon {\cal D}( \varphi(m)) \to {\mathbb{R}}$$

elemento del espacio vectorial tangente ${\cal F}_{\varphi (m)}$.

Este resultado nos lleva a:

Teorema 2.1 (y definición)   Sean $M, N$ variedades $C^k$ y $\varphi \colon M \to N$ una aplicación diferenciable en un punto $m \in M$. Observamos que en virtud del teorema 5.2.4 si $g \in {\cal D}(\varphi(m))$ vale $g \circ \varphi \in {\cal D}(m)$ (cuyo dominio satisface la identidad, ${\rm Dom\ }(g \circ \varphi) = \varphi^{-1} ( \mbox{\rm Dom } g )$).

$\forall \, \vec u \in M_m$ la funcional ${\cal D}(\varphi(m)) \to {\mathbb{R}}$ dada por:

$$\fbox{${\displaystyle g \mapsto \vec u \cdot ( g \circ \varphi)}$}$$

es un vector tangente a la variedad $N$ en el punto $\varphi(m)$, elemento del espacio vectorial $N_{\varphi(m)}$. Este vector tangente se designa por $d \varphi(m) \vec u$. Así pues:

$$\fbox{${\displaystyle \left( d \varphi(m) \vec u \right) \cdo... ...g \circ \varphi) \quad \forall \, g \in {\cal D}(\varphi(m))}$}$$

La aplicación $d \varphi(m) \colon M_m \to N_{\varphi (m)}$, $g \mapsto \vec u \cdot ( g \circ \varphi)$, definida por esta fórmula es una aplicación lineal del espacio vectorial $M_m$ en el espacio vectorial $N_{\varphi(m)}$. Se llama la DIFERENCIAL DE LA APLICACIÓN EN EL PUNTO .

Demostración

1. Sea $L$ la funcional: ${\cal D}(\varphi(m)) \to {\mathbb{R}}$ dada por:
   
   $$L(g) = \colon \vec u \cdot (g \circ \varphi)\quad \forall \, g \in {\cal D}(\varphi(m))$$
   
   
   Comprobemos que $L$ goza de las tres propiedades leibnizianas.
   1. $\forall \, g_1, \, g_2 \in {\cal D}(\varphi(m))$ y $\forall \, \alpha_1,\, \alpha_2\in {\mathbb{R}}$ se verifica:
      $$\begin{eqnarray*} L ( \alpha_1 g_1 + \alpha_2 g_2) &=& \vec u \cdot \left( ( \al... ...t ( g_2 \circ \varphi) \\ &=& \alpha _1 L g_1 + \alpha_2 L g_2 \end{eqnarray*}$$
      
      
      Luego $L$ goza de la propiedad leibniziana 1).
   2. $\forall \, g_1, \, g_2 \in {\cal D}(\varphi(m))$ vale:
      $$\begin{eqnarray*} L (g_1 g_2 ) &=& \vec u \cdot \left( (g_1 g_2 ) \circ \varphi\... ...\varphi) \\ &=& g_2 (\varphi(m)) Lg_1 + g_1 (\varphi(m)) L g_2 \end{eqnarray*}$$
      
      
      Luego $L$ goza de la propiedad leibniziana 2).
   3. Sea $g \in {\cal D}(\varphi(m))$ tal que $g (\varphi(m)) =0$ y sea $h \in {\cal C}( \varphi(m))$. Estas hipótesis implican $g \circ \varphi \in {\cal D}(m)$, $(g \circ \varphi)(m) =0$ y $h \circ \varphi \in \varphi(m)$. Tenemos:
      $$\begin{eqnarray*} L(hg) &=& \vec u \cdot \left( (hg) \circ \varphi \right) \\ &... ...i)(m) \vec u \cdot ( g \circ \varphi) \\ &=& h(\varphi(m)) L g \end{eqnarray*}$$
      
      

   De (i), (ii), (iii) se sigue que, en efecto, $L \in N_{\varphi(m)}$.
2. Cambiando de notación designemos por $d \varphi(m) \vec u$ a la funcional $L$ del inciso a), vector tangente a la variedad $N$ en el punto $\varphi(m)$. Debemos probar que la aplicación $d \varphi(m) \colon M_m \to N_{\varphi (m)}$ es bilineal.

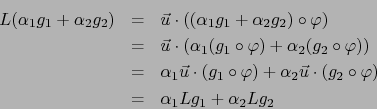
   Ahora bien, $\forall \, \vec{u}_1,\, \vec{u}_2 \in M_m$, $\forall \, \alpha_1,\, \alpha_2\in {\mathbb{R}}$ y $\forall \, g \in {\cal D}(\varphi (m))$ se verifica:

   $$\begin{eqnarray*} \left( d \varphi(m) ( \alpha_1 \vec{u}_1 + \alpha_2 \vec{u}_2)... ...) \vec{u}_1) \cdot g + \alpha_2 (d \varphi(m) \vec{u}_2) \cdot g \end{eqnarray*}$$
   
   
   o sea, quitando el argumento $g$:
   
   $$d\varphi(m) (\alpha_1 \vec{u}_1 + \alpha_2 \vec{u}_2) = \alpha_1 d \varphi(m) (\vec{u}_1) + \alpha_2 d \varphi(m) \vec{u}_2$$
   
   
   La aplicación $d \varphi (m)$ es, pues, efectivamente lineal. $\quad\Box$

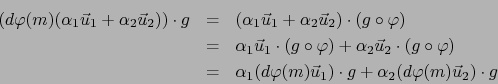
Observación
La permanencia de la definición de $d \varphi (m)$ está garantizada por las consideraciones heurísticas que preceden.

Siguiente: Caso de variedades con Arriba: Diferenciación Anterior: Diferenciación